不等式的性质(2)[下学期]
文档属性
| 名称 | 不等式的性质(2)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 439.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-05-24 21:36:00 | ||
图片预览






文档简介
课件17张PPT。9.1.2不等式的性质(二)回忆:不等式的性质。
不等式的性质1:
如果a>b,那么a+c>b+c,a-c>b-c。
不等式的性质2:
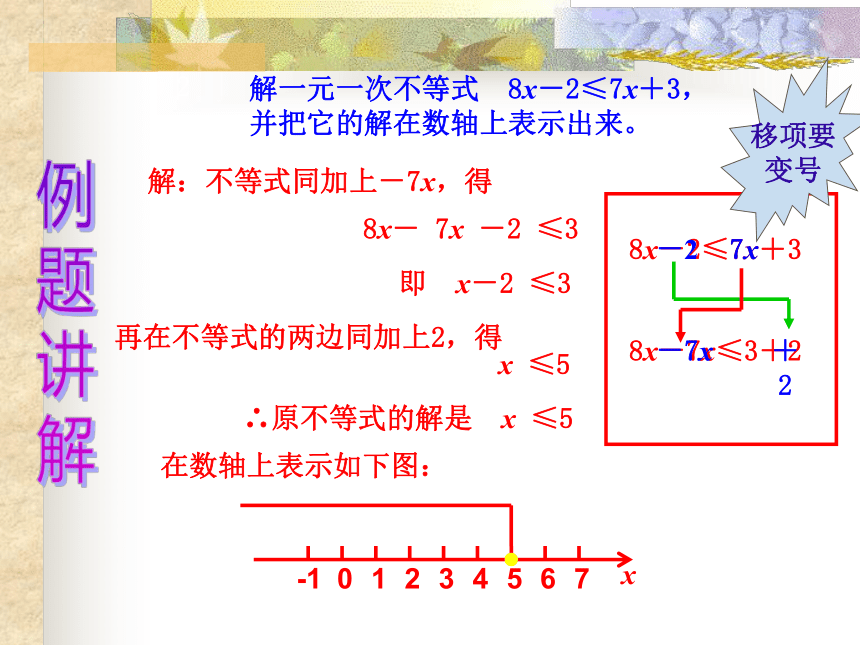
如果a>b,并且c>0,那么ac>bc不等式的性质3:如果a>b,并且c<0,那么ac0C<0解:不等式同加上-7x,得 例
题
讲
解8x- 7x -2 ≤3即 x-2 ≤3再在不等式的两边同加上2,得x ≤5∴原不等式的解是 x ≤5在数轴上表示如下图:-2+27x-7x移项要
变号例2 解不等式
3(1+x)>2(1+2x)3(1+x)>2(1+2x)变
形解:去括号,得 3+3x>2+4x移项,得 3x-4x> 2-3合并同类项,得 -x>-1∴ 原不等式的解是 x<1 写不等式的解时,要把表示未知数的字母写在不等号的左边。解下列不等式:并把解集在数轴上表示出来练习例4例3情境V+3×5×3 ≤ 3×5×10
V+45 ≤150
V ≤105 又因为新注入水的体积V不是负数,
因此,V的取值范围是 0≤ V ≤105.情境 解:如图,设a,b,c为任意一个三角形的三条边的边长,则 a+b>c,b+c>a,c+a>b.
由式子a+b >c移项可得
a>c-b ,b>c-a.
类似地,由式子b+c>a及c+a>b移项可得
c>a-b, b>a-c c>b-a,a >b-c.
这就是说,三角形中任意两边之差小于第三边学到了哪些知识?
在思想、方法上你有什么收获?
在解不等式时,要注意什么问题?小结再见解:设A型钢板和B型钢板的面积分别为x和y.
于是方案1用料面积为4x+8y,方案2用料面积为3x+9y.∵x>y ∴(4x+8y)-(3x+9y)=x-y>0
∴4x+8y >3x+9y
答:从省料角度考虑,应选方案2.情境综合运用P134解: 39.98≤ V ≤40.02.解:设蛋白质的含量为x g,
由题意,得 x ≥300×0.6%
x ≥1.8
答:蛋白质的含量不小于1.8 g.综合运用P135解:由题意,得 12x+40≤1000
12x ≤960
x ≤80
答:他们的平均体重x不大于80kg.综合运用P135解:若对调后得到的两位数比原来的两位数大,
则 (10a+b)-(10b+a)>0,即 9a-9b>0, a>b.
若对调后得到的两位数比原来的两位数小,
则(10a+b)-(10b+a)<0,即 a若对调后得到的两位数等于原来的两位数,
则(10a+b)-(10b+a)=0,即 a=b.
拓广探索P135解:黄金的质量(克) ≥0.9a;白银的质量(克) ≤0.1a.
当首饰的质量为定值时,黄金含量越多,首饰的体积越小.
设首饰的体积为V cm3,
则
V ≤0.06a答:这件首饰的体积不大于0.06a克.拓广探索P135解:设李明的冲刺速度为x m/s,
则
x>4.4答:李明的冲刺速度大于4.4 m/s,才能够在张华之前
到达终点。
不等式的性质1:
如果a>b,那么a+c>b+c,a-c>b-c。
不等式的性质2:
如果a>b,并且c>0,那么ac>bc不等式的性质3:如果a>b,并且c<0,那么ac
题
讲
解8x- 7x -2 ≤3即 x-2 ≤3再在不等式的两边同加上2,得x ≤5∴原不等式的解是 x ≤5在数轴上表示如下图:-2+27x-7x移项要
变号例2 解不等式
3(1+x)>2(1+2x)3(1+x)>2(1+2x)变
形解:去括号,得 3+3x>2+4x移项,得 3x-4x> 2-3合并同类项,得 -x>-1∴ 原不等式的解是 x<1 写不等式的解时,要把表示未知数的字母写在不等号的左边。解下列不等式:并把解集在数轴上表示出来练习例4例3情境V+3×5×3 ≤ 3×5×10
V+45 ≤150
V ≤105 又因为新注入水的体积V不是负数,
因此,V的取值范围是 0≤ V ≤105.情境 解:如图,设a,b,c为任意一个三角形的三条边的边长,则 a+b>c,b+c>a,c+a>b.
由式子a+b >c移项可得
a>c-b ,b>c-a.
类似地,由式子b+c>a及c+a>b移项可得
c>a-b, b>a-c c>b-a,a >b-c.
这就是说,三角形中任意两边之差小于第三边学到了哪些知识?
在思想、方法上你有什么收获?
在解不等式时,要注意什么问题?小结再见解:设A型钢板和B型钢板的面积分别为x和y.
于是方案1用料面积为4x+8y,方案2用料面积为3x+9y.∵x>y ∴(4x+8y)-(3x+9y)=x-y>0
∴4x+8y >3x+9y
答:从省料角度考虑,应选方案2.情境综合运用P134解: 39.98≤ V ≤40.02.解:设蛋白质的含量为x g,
由题意,得 x ≥300×0.6%
x ≥1.8
答:蛋白质的含量不小于1.8 g.综合运用P135解:由题意,得 12x+40≤1000
12x ≤960
x ≤80
答:他们的平均体重x不大于80kg.综合运用P135解:若对调后得到的两位数比原来的两位数大,
则 (10a+b)-(10b+a)>0,即 9a-9b>0, a>b.
若对调后得到的两位数比原来的两位数小,
则(10a+b)-(10b+a)<0,即 a
则(10a+b)-(10b+a)=0,即 a=b.
拓广探索P135解:黄金的质量(克) ≥0.9a;白银的质量(克) ≤0.1a.
当首饰的质量为定值时,黄金含量越多,首饰的体积越小.
设首饰的体积为V cm3,
则
V ≤0.06a答:这件首饰的体积不大于0.06a克.拓广探索P135解:设李明的冲刺速度为x m/s,
则
x>4.4答:李明的冲刺速度大于4.4 m/s,才能够在张华之前
到达终点。
