2.1.2 正弦与余弦同步练习(含解析)
文档属性
| 名称 | 2.1.2 正弦与余弦同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 21:14:59 | ||
图片预览


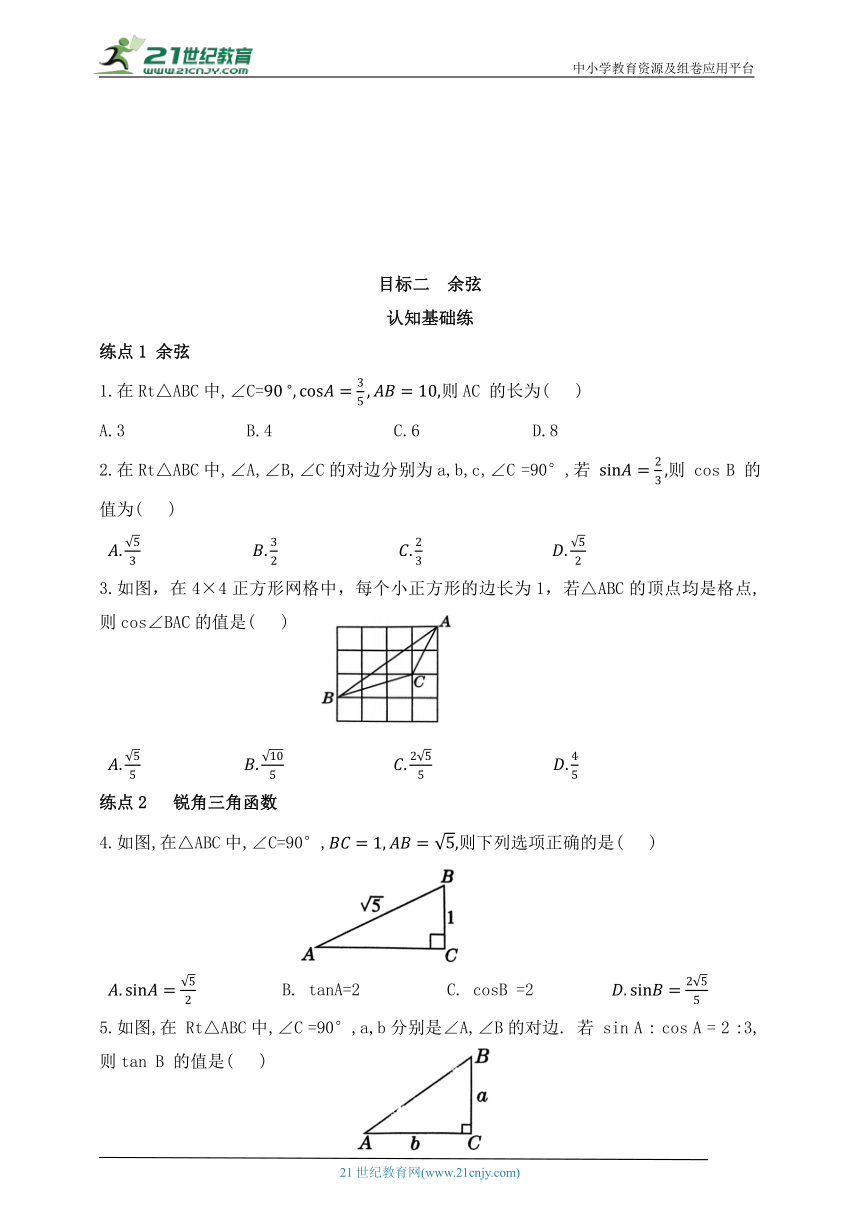

文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
1 锐角三角函数
第2课时 正弦与余弦
目标一 正弦
认知基础练
练点1 正弦的定义
1.在Rt△ABC中,若∠C=90°,AC=5,BC=12,则 sin A 的值为__________.
2.如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB,D为垂足.若AC =8,BC=6,则 sin∠ACD的值为( )
练点2 正弦的应用
如图,在平面直角坐标系内有一点 P(3,4),连接OP,则 OP与x轴正方向所夹锐角α的正弦值是( )
4.如图所示是一个左右两侧不等长的跷跷板,跷板 AB长为4米,支柱 OH垂直地面.如图①,当AB的一端A 接触地面时,AB与地面的夹角的正弦值为 如图②,当AB的另一端B接触地面时,AB 与地面的夹角的正弦值为 则支柱 OH的长为( )
A.0.5米
B.0.6米
C.0.8米
米
纠易错 不能正确构造直角三角形而误用正弦
5.】如图,在4×5 的正方形网格中,每个小正方形的边长都是1,△ABC 的顶点都在这些小正方形的顶点上,那么sin ∠ACB的值为( )
思维发散练
发散点1 利用正弦的定义求正弦值
6.如图,点M 是正方形ABCD的边 CD上一点,连接AM,作 DE⊥AM于点E,BF⊥AM于点F,连接 BE.
(1)求证:AE=BF;
(2)已知 AF=2,四边形 ABED 的面积为24,求∠EBF的正弦值.
发散点2 利用正弦值求线段的长
7.学科素养模型观念如图,一座钢结构桥梁的框架是△ABC,水平横梁 BC 长 18 m,中柱 AD高6m,其中D是 BC 的中点,且AD⊥BC.
(1)求 sin B 的值;
(2)现需要加装支架DE,EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为 F,求支架EF的长.
目标二 余弦
认知基础练
练点1 余弦
1.在Rt△ABC中,∠C=则AC 的长为( )
A.3 B.4 C.6 D.8
2.在Rt△ABC中,∠A,∠B,∠C的对边分别为a,b,c,∠C =90°,若 则 cos B 的值为( )
3.如图,在4×4正方形网格中,每个小正方形的边长为1,若△ABC的顶点均是格点,则cos∠BAC的值是( )
练点2 锐角三角函数
4.如图,在△ABC中,∠C=90°,则下列选项正确的是( )
B. tanA=2 C. cosB =2
5.如图,在 Rt△ABC中,∠C =90°,a,b分别是∠A,∠B的对边. 若 sin A : cos A = 2 :3,则tan B 的值是( )
纠易错 忽视锐角的余弦值的取值范围而致错
6.已知 x=cosα(α为锐角)满足方程2x -5x+2=0,求 cosα的值.
思维发散练
发散点1 利用三角函数的定义求三角函数值
7.如图,在平面直角坐标系内,O为原点,点A 的坐标为(10,0),点B在第一象限内, 求:
(1)点B的坐标;
(2)cos∠BAO 的值.
发散点2 利用三角函数的定义求线段的长
8.如图,在△ABC 中,
(1)求边AC 的长和 cos C 的值;
(2)设边BC 的垂直平分线与边AB,BC 的交点分别为D,F,求DF 的长.
参考答案
目标一 正弦
【点拨】在 Rt△ABC中,根据勾股定理得,AB=
2. C 【点拨】∵CD⊥AB,∴∠CDA =90°.
∵∠ACD+∠BCD=90°,∠B+∠BCD=90°,∴∠ACD=∠B.
在 Rt△ABC中,
故选 C.
3. D【点拨】过点P作PM⊥x轴于点M.∵P的坐标为(3,4),∴PM=4,OM=3,由勾股定理得 OP=5, 故选 D.
4. C 【点拨】在 Rt△AOH 中, 2OH.同理可得OB=3OH.
∵AB=4,∴2OH+3OH=4,解得 OH=0.8.故选 C.
5. D 【点拨】过点 A 作AD⊥BC 于点D,则∠ADC= .故选 D.
6.(1)【证明】∵四边形 ABCD为正方形,∴AB=AD,∠BAD=90°.∴∠BAF+∠DAE=90°.
∵DE⊥AM,BF⊥AM,∴∠DEA =∠AFB=90°.∴∠ADE+∠DAE=90°.∴∠BAF=∠ADE.
在△DEA 和△AFB中, ∴△DEA≌△AFB(AAS).∴AE=BF.
(2)【解】设AE=x,则 BF=x.∵△DEA≌△AFB,∴DE=AF=2.
∵四边形ABED的面积为24,解得x1=6,x2= -8(舍去).∴AE=BF=6.∴EF=AE-AF=6-2=4.
在 Rt△EFB 中,
7.【解】(1)在 Rt△ABD中,∵
(2)在 Rt△BEF中.
又∵
答:支架EF的长为4m .
目标二 余弦
1. C 【点拨】 解得AC=6,故选 C.
2. C 【点拨】由题知 故选 C.
3. C 【点拨】延长AC到D,连接BD.∵AD =20,BD =5,AB = 25,∴ AD +BD = AB ,
∴∠ADB = 90°,故选 C.
4. D 【点拨】在△ABC中,∠C=90°,BC=1,AB= ,
故选 D.
5. B 【点拨】∵在Rt△ABC中,∠C=90°,sinA:cosA=2故选B.
6.【解】解方程2x -5x+2=0,得
∵α为锐角,
点易错 本题易忽略 cosα(α为锐角) 的取值范围是0<cosα<1,而错得cosα=2或
7.【解】如图,过点 B作BC⊥OA 于点 C.
点B的坐标为(4,3).
(2)易知 OA =10.
8.【解】(1)如图,过点A作AE⊥BC 于点E,则∠AEB=∠AEC=90°.
在 Rt△ABE中, 设 AE=3x,则BE=4x.∵AE +BE =AB ,
∴(3x) +(4x) =5 ,解得x=1.∴AE=3,BE=4.∴EC=BC-BE=5-4=1.
(2)∵DF垂直平分 BC,
在Rt△BFD中,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
1 锐角三角函数
第2课时 正弦与余弦
目标一 正弦
认知基础练
练点1 正弦的定义
1.在Rt△ABC中,若∠C=90°,AC=5,BC=12,则 sin A 的值为__________.
2.如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB,D为垂足.若AC =8,BC=6,则 sin∠ACD的值为( )
练点2 正弦的应用
如图,在平面直角坐标系内有一点 P(3,4),连接OP,则 OP与x轴正方向所夹锐角α的正弦值是( )
4.如图所示是一个左右两侧不等长的跷跷板,跷板 AB长为4米,支柱 OH垂直地面.如图①,当AB的一端A 接触地面时,AB与地面的夹角的正弦值为 如图②,当AB的另一端B接触地面时,AB 与地面的夹角的正弦值为 则支柱 OH的长为( )
A.0.5米
B.0.6米
C.0.8米
米
纠易错 不能正确构造直角三角形而误用正弦
5.】如图,在4×5 的正方形网格中,每个小正方形的边长都是1,△ABC 的顶点都在这些小正方形的顶点上,那么sin ∠ACB的值为( )
思维发散练
发散点1 利用正弦的定义求正弦值
6.如图,点M 是正方形ABCD的边 CD上一点,连接AM,作 DE⊥AM于点E,BF⊥AM于点F,连接 BE.
(1)求证:AE=BF;
(2)已知 AF=2,四边形 ABED 的面积为24,求∠EBF的正弦值.
发散点2 利用正弦值求线段的长
7.学科素养模型观念如图,一座钢结构桥梁的框架是△ABC,水平横梁 BC 长 18 m,中柱 AD高6m,其中D是 BC 的中点,且AD⊥BC.
(1)求 sin B 的值;
(2)现需要加装支架DE,EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为 F,求支架EF的长.
目标二 余弦
认知基础练
练点1 余弦
1.在Rt△ABC中,∠C=则AC 的长为( )
A.3 B.4 C.6 D.8
2.在Rt△ABC中,∠A,∠B,∠C的对边分别为a,b,c,∠C =90°,若 则 cos B 的值为( )
3.如图,在4×4正方形网格中,每个小正方形的边长为1,若△ABC的顶点均是格点,则cos∠BAC的值是( )
练点2 锐角三角函数
4.如图,在△ABC中,∠C=90°,则下列选项正确的是( )
B. tanA=2 C. cosB =2
5.如图,在 Rt△ABC中,∠C =90°,a,b分别是∠A,∠B的对边. 若 sin A : cos A = 2 :3,则tan B 的值是( )
纠易错 忽视锐角的余弦值的取值范围而致错
6.已知 x=cosα(α为锐角)满足方程2x -5x+2=0,求 cosα的值.
思维发散练
发散点1 利用三角函数的定义求三角函数值
7.如图,在平面直角坐标系内,O为原点,点A 的坐标为(10,0),点B在第一象限内, 求:
(1)点B的坐标;
(2)cos∠BAO 的值.
发散点2 利用三角函数的定义求线段的长
8.如图,在△ABC 中,
(1)求边AC 的长和 cos C 的值;
(2)设边BC 的垂直平分线与边AB,BC 的交点分别为D,F,求DF 的长.
参考答案
目标一 正弦
【点拨】在 Rt△ABC中,根据勾股定理得,AB=
2. C 【点拨】∵CD⊥AB,∴∠CDA =90°.
∵∠ACD+∠BCD=90°,∠B+∠BCD=90°,∴∠ACD=∠B.
在 Rt△ABC中,
故选 C.
3. D【点拨】过点P作PM⊥x轴于点M.∵P的坐标为(3,4),∴PM=4,OM=3,由勾股定理得 OP=5, 故选 D.
4. C 【点拨】在 Rt△AOH 中, 2OH.同理可得OB=3OH.
∵AB=4,∴2OH+3OH=4,解得 OH=0.8.故选 C.
5. D 【点拨】过点 A 作AD⊥BC 于点D,则∠ADC= .故选 D.
6.(1)【证明】∵四边形 ABCD为正方形,∴AB=AD,∠BAD=90°.∴∠BAF+∠DAE=90°.
∵DE⊥AM,BF⊥AM,∴∠DEA =∠AFB=90°.∴∠ADE+∠DAE=90°.∴∠BAF=∠ADE.
在△DEA 和△AFB中, ∴△DEA≌△AFB(AAS).∴AE=BF.
(2)【解】设AE=x,则 BF=x.∵△DEA≌△AFB,∴DE=AF=2.
∵四边形ABED的面积为24,解得x1=6,x2= -8(舍去).∴AE=BF=6.∴EF=AE-AF=6-2=4.
在 Rt△EFB 中,
7.【解】(1)在 Rt△ABD中,∵
(2)在 Rt△BEF中.
又∵
答:支架EF的长为4m .
目标二 余弦
1. C 【点拨】 解得AC=6,故选 C.
2. C 【点拨】由题知 故选 C.
3. C 【点拨】延长AC到D,连接BD.∵AD =20,BD =5,AB = 25,∴ AD +BD = AB ,
∴∠ADB = 90°,故选 C.
4. D 【点拨】在△ABC中,∠C=90°,BC=1,AB= ,
故选 D.
5. B 【点拨】∵在Rt△ABC中,∠C=90°,sinA:cosA=2故选B.
6.【解】解方程2x -5x+2=0,得
∵α为锐角,
点易错 本题易忽略 cosα(α为锐角) 的取值范围是0<cosα<1,而错得cosα=2或
7.【解】如图,过点 B作BC⊥OA 于点 C.
点B的坐标为(4,3).
(2)易知 OA =10.
8.【解】(1)如图,过点A作AE⊥BC 于点E,则∠AEB=∠AEC=90°.
在 Rt△ABE中, 设 AE=3x,则BE=4x.∵AE +BE =AB ,
∴(3x) +(4x) =5 ,解得x=1.∴AE=3,BE=4.∴EC=BC-BE=5-4=1.
(2)∵DF垂直平分 BC,
在Rt△BFD中,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
