2.1.1 正切同步练习（含解析）

中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
1 锐角三角函数
第1课时 正切
认知基础练
练点1 正切的定义
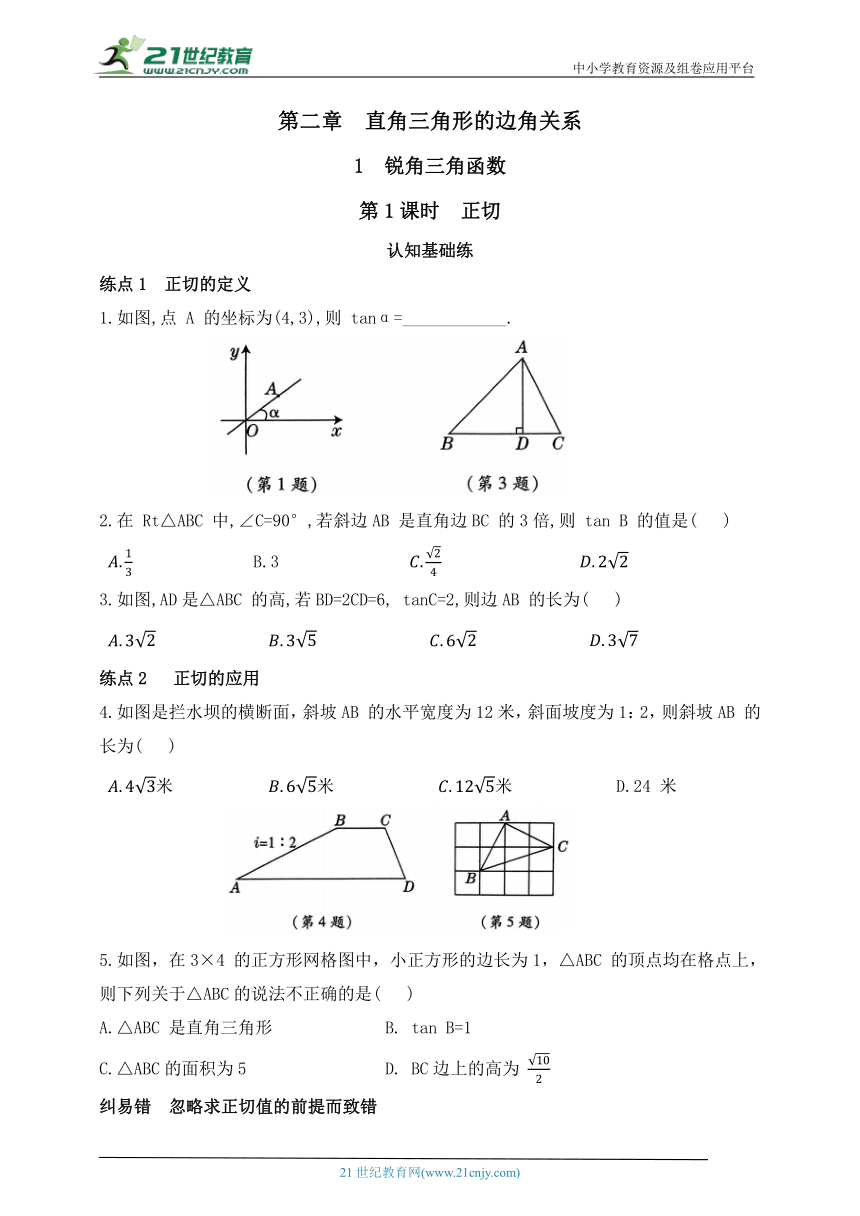
1.如图,点 A 的坐标为(4,3),则 tanα=____________.
2.在 Rt△ABC 中,∠C=90°,若斜边AB 是直角边BC 的3倍,则 tan B 的值是( )
B.3
3.如图,AD是△ABC 的高,若BD=2CD=6, tanC=2,则边AB 的长为( )
练点2 正切的应用
4.如图是拦水坝的横断面，斜坡AB 的水平宽度为12米，斜面坡度为1：2，则斜坡AB 的长为( )
米 米 米 D.24 米
5.如图，在3×4 的正方形网格图中，小正方形的边长为1，△ABC 的顶点均在格点上，则下列关于△ABC的说法不正确的是( )
A.△ABC 是直角三角形 B. tan B=1
C.△ABC的面积为5 D. BC边上的高为
纠易错 忽略求正切值的前提而致错
6.在等腰三角形ABC中,AB=AC=10,BC =12,则 tan B=______________.
思维发散练
发散点 1 利用正切的定义求正切值(等角代换法)
7.如图,在 Rt△ABC中,∠ABC=90°,AB(1)求证:四边形AECF是菱形;
(2)若 则tan∠BCF的值为_____________.
发散点2 利用正切的定义求面积
8.如图，在平行四边形ABCD中，点E,F分别在 AD,BC上,且 ED = BF,连接AF,CE,AC,EF,且AC与EF相交于点 O.
(1)求证:四边形 AFCE 是平行四边形;
(2)若AC平分 求四边形AFCE的面积.
参考答案
【点拨】过点 A 作AH⊥x轴于点H.∵点A 的坐标为(4,3),∴AH=3,OH=4, 故答案为
2. D 【点拨】在 Rt△ABC 中,设BC =x(x>0),则
故选 D.
3. C 【点拨】∵ 故选C.
4. B 【点拨】如图,过 B作BCBE⊥AD于点 E.∵斜面坡度为1:2,AE=12米,∴BE = 6米. 在 Rt△ABE 中, (米).故选 B.
5. C 【点拨】∵小正方形的边长为1，∴ 由勾股定理得 是直角三角形，故选项A 正确，不符合题意； 故选项 B 正确，不符合题意；
故选项C错误，符合题意；设BC 边上的高为h，则有 解得 故选项D正确，不符合题意.故选C.
点易错 本题易忽略求正切值的前提条件是将∠B放在一个直角三角形中.
7.(1)【证明】∵点 D是AC的中点,∴AD=CD.
∵DF=DE,∴四边形AECF是平行四边形.
又∵DE⊥AC,∴平行四边形AECF是菱形.
【点拨】设BE=a,则CE=4a.由菱形的性质得AE = CE=4a,AE∥CF,则∠BEA =∠BCF.
再由勾股定理得 然后由锐角三角函数的定义即可得出结论.
8.(1)【证明】∵四边形 ABCD是平行四边形,∴AD=BC,AE∥FC.
又∵ED=BF,∴AD-ED=BC-BF.∴AE=FC.
∴四边形AFCE是平行四边形.
(2)【解】∵AE∥FC,∴∠EAC=∠ACF.
∵AC平分∠FAE,∴∠EAC=∠FAC,∴∠ACF=∠FAC.∴AF=FC.∴平行四边形AFCE是菱形.
在 Rt△AOE中,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)