三角形外角和[下学期]
图片预览

文档简介
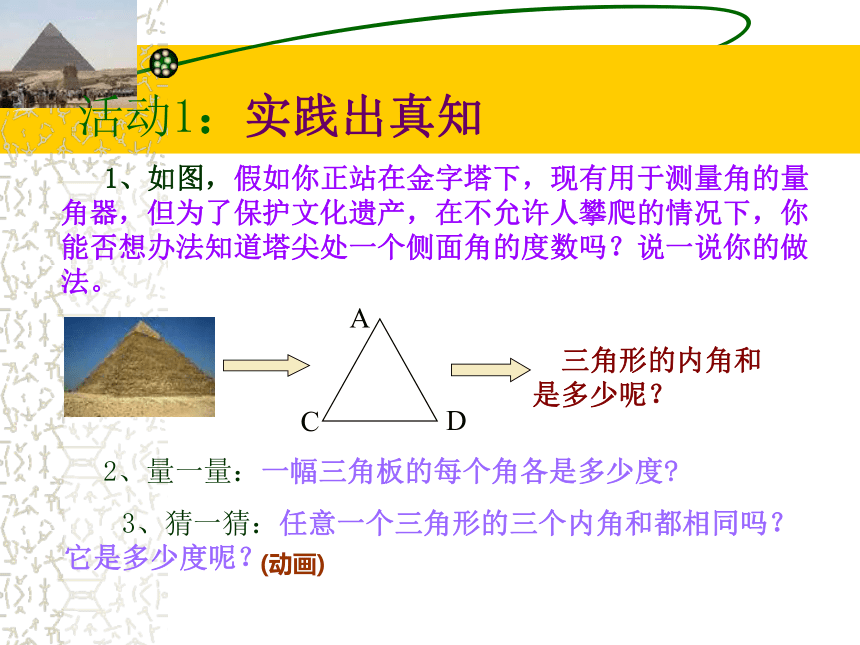
课件11张PPT。虎威镇中学校 马世军 三角形的内角 1、如图,假如你正站在金字塔下,现有用于测量角的量角器,但为了保护文化遗产,在不允许人攀爬的情况下,你能否想办法知道塔尖处一个侧面角的度数吗?说一说你的做法。 三角形的内角和是多少呢? 2、量一量:一幅三角板的每个角各是多少度? 3、猜一猜:任意一个三角形的三个内角和都相同吗?它是多少度呢?活动1:实践出真知(动画) 4、动动手,仔细观察:
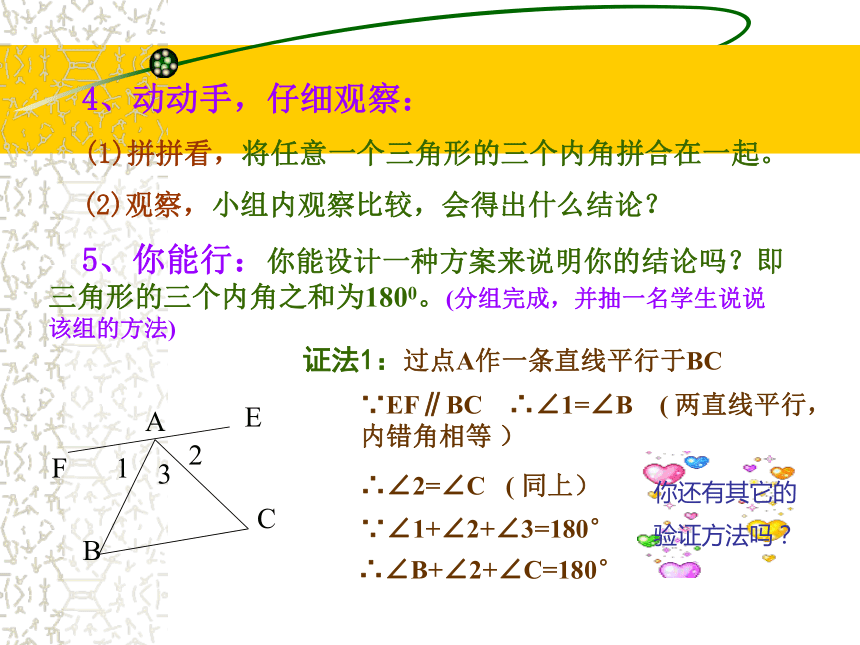
(1)拼拼看,将任意一个三角形的三个内角拼合在一起。
(2)观察,小组内观察比较,会得出什么结论? 5、你能行:你能设计一种方案来说明你的结论吗?即三角形的三个内角之和为1800。(分组完成,并抽一名学生说说该组的方法)证法1:过点A作一条直线平行于BC∵EF∥BC ∴∠1=∠B ( 两直线平行,内错角相等 )∴∠2=∠C ( 同上)∵∠1+∠2+∠3=180° ∴∠B+∠2+∠C=180°你还有其它的
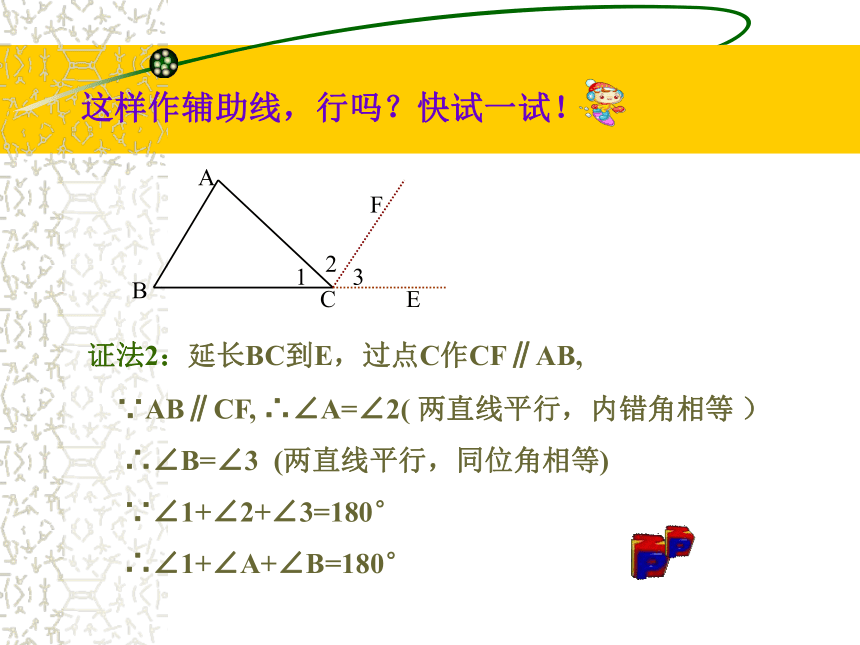
验证方法吗? ∵AB∥CF, ∴∠A=∠2( 两直线平行,内错角相等 )
∴∠B=∠3 (两直线平行,同位角相等)
∵∠1+∠2+∠3=180°
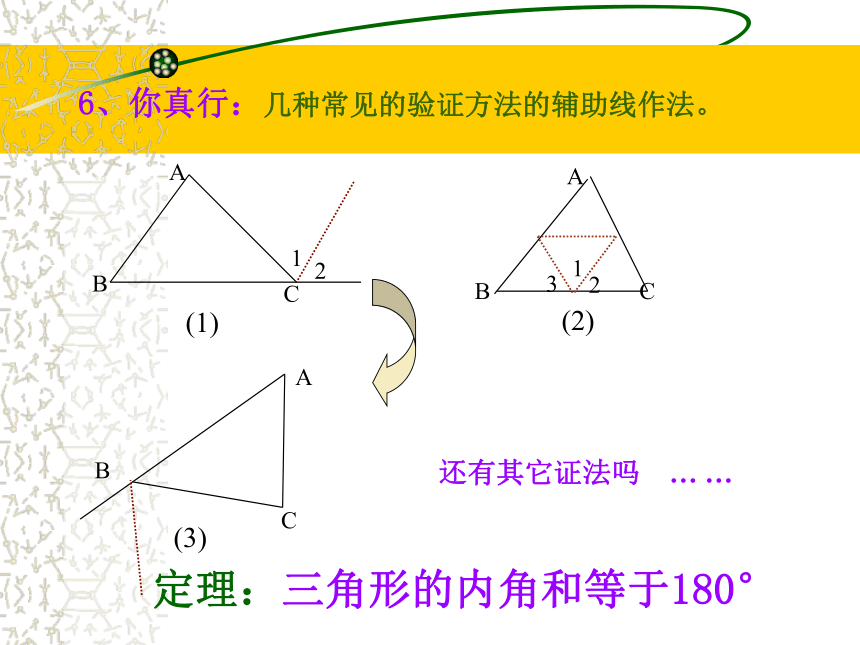
∴∠1+∠A+∠B=180°这样作辅助线,行吗?快试一试!证法2:延长BC到E,过点C作CF∥AB, 6、你真行:几种常见的验证方法的辅助线作法。ABC121ABC32(1)(2)ABC(3)还有其它证法吗 … …定理:三角形的内角和等于180°活动2:学会应用 例1:在△ABC中,∠A :∠ B: ∠ C= ∠ 1: ∠ 2: ∠ 3,求∠ ABC的度数。 解法一:由已知可设∠ A=x0, ∠ B=2x0, ∠ C=3x0,由三角形的内角和为1800可得:
x+2x+3x=180 解得x=30,
∴ ∠ A=300, ∠ B=600, ∠ C=900。 解法二: ∵ ∠ A :∠ B: ∠ C= ∠ 1: ∠ 2: ∠ 3,
∴ ∠ B=2 ∠ A, ∠ C=3 ∠ A
又∠ A +∠ B+ ∠ C=1800
∴ ∠ A+2 ∠ A+3 ∠ A=1800
∴ ∠ A=300, ∠ B=600, ∠ C=900。 例2:如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向,从C岛看A、B两岛的视角∠ACB是多少度?解 :∠CAB=∠DAB-∠DAC=800-500=300
∵AD∥BE ∴∠DAB+∠ABE=180°(两直线平行,同旁内角互补)
∴∠ABE=1800-∠BAD=1800-800=1000,
∴∠ABC=∠ABE-∠EBC=1000-400=600。
在△ABC中, ∠ACB=1800-∠ABC- ∠ CAB=
1800-600-300=900
答:从C岛看A.B两岛的俯角∠ACB是90°。4005003、完成教材80页练习1、2题。1、填空
(1) 在△ABC中,∠A=30°∠B=500, 则∠C=____。
(2) 在△ABC中,∠C=90°∠B=500, 则∠A=____。
(3)在△ABC中, ∠A=400,∠A=2∠B,则∠C=____。
(4)在△ABC中, ∠A等于直角的一半,∠B等于直角的 ,则∠C=__。活动3:比一比,赛一赛你真行!看哪一组做得又对又快!2、如图,在△ABC中, ∠ABC=70°, ∠C=65°,BD⊥AC于D, 求∠ABD, ∠CBD的度数。活动4:指导实践 1、一块模板如图所示,按规定AF、DE的延长线相交成850角,因交点不在板上,不便测量,工人师傅连结AD,测得∠ FAD=340,ADE=630,这时就知道AF、DE的延长线相交所成的角是不是符合规定?为什么? 2、金字塔一侧面角的顶角到底是多少度呢?请翻到书第35页吧!做一做!(1)三角形内角和定理实践探究及其运用。回顾与小结本节课里你学到了什么???(2)学好数学方法及信心。课后再探索1、一个三角形最多有几个直角?为什么?
2、一个三角形最多有几个钝角?为什么?
3、一个三角形最多有几个锐角?最少有几个锐角?
4、你能否利用三角形的内角和,求出四边形、五边形的内角和?
(1)拼拼看,将任意一个三角形的三个内角拼合在一起。
(2)观察,小组内观察比较,会得出什么结论? 5、你能行:你能设计一种方案来说明你的结论吗?即三角形的三个内角之和为1800。(分组完成,并抽一名学生说说该组的方法)证法1:过点A作一条直线平行于BC∵EF∥BC ∴∠1=∠B ( 两直线平行,内错角相等 )∴∠2=∠C ( 同上)∵∠1+∠2+∠3=180° ∴∠B+∠2+∠C=180°你还有其它的
验证方法吗? ∵AB∥CF, ∴∠A=∠2( 两直线平行,内错角相等 )
∴∠B=∠3 (两直线平行,同位角相等)
∵∠1+∠2+∠3=180°
∴∠1+∠A+∠B=180°这样作辅助线,行吗?快试一试!证法2:延长BC到E,过点C作CF∥AB, 6、你真行:几种常见的验证方法的辅助线作法。ABC121ABC32(1)(2)ABC(3)还有其它证法吗 … …定理:三角形的内角和等于180°活动2:学会应用 例1:在△ABC中,∠A :∠ B: ∠ C= ∠ 1: ∠ 2: ∠ 3,求∠ ABC的度数。 解法一:由已知可设∠ A=x0, ∠ B=2x0, ∠ C=3x0,由三角形的内角和为1800可得:
x+2x+3x=180 解得x=30,
∴ ∠ A=300, ∠ B=600, ∠ C=900。 解法二: ∵ ∠ A :∠ B: ∠ C= ∠ 1: ∠ 2: ∠ 3,
∴ ∠ B=2 ∠ A, ∠ C=3 ∠ A
又∠ A +∠ B+ ∠ C=1800
∴ ∠ A+2 ∠ A+3 ∠ A=1800
∴ ∠ A=300, ∠ B=600, ∠ C=900。 例2:如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向,从C岛看A、B两岛的视角∠ACB是多少度?解 :∠CAB=∠DAB-∠DAC=800-500=300
∵AD∥BE ∴∠DAB+∠ABE=180°(两直线平行,同旁内角互补)
∴∠ABE=1800-∠BAD=1800-800=1000,
∴∠ABC=∠ABE-∠EBC=1000-400=600。
在△ABC中, ∠ACB=1800-∠ABC- ∠ CAB=
1800-600-300=900
答:从C岛看A.B两岛的俯角∠ACB是90°。4005003、完成教材80页练习1、2题。1、填空
(1) 在△ABC中,∠A=30°∠B=500, 则∠C=____。
(2) 在△ABC中,∠C=90°∠B=500, 则∠A=____。
(3)在△ABC中, ∠A=400,∠A=2∠B,则∠C=____。
(4)在△ABC中, ∠A等于直角的一半,∠B等于直角的 ,则∠C=__。活动3:比一比,赛一赛你真行!看哪一组做得又对又快!2、如图,在△ABC中, ∠ABC=70°, ∠C=65°,BD⊥AC于D, 求∠ABD, ∠CBD的度数。活动4:指导实践 1、一块模板如图所示,按规定AF、DE的延长线相交成850角,因交点不在板上,不便测量,工人师傅连结AD,测得∠ FAD=340,ADE=630,这时就知道AF、DE的延长线相交所成的角是不是符合规定?为什么? 2、金字塔一侧面角的顶角到底是多少度呢?请翻到书第35页吧!做一做!(1)三角形内角和定理实践探究及其运用。回顾与小结本节课里你学到了什么???(2)学好数学方法及信心。课后再探索1、一个三角形最多有几个直角?为什么?
2、一个三角形最多有几个钝角?为什么?
3、一个三角形最多有几个锐角?最少有几个锐角?
4、你能否利用三角形的内角和,求出四边形、五边形的内角和?
