2.4.2 已知边、角(或三角函数值)解直角三角形同步练习(含解析)
文档属性
| 名称 | 2.4.2 已知边、角(或三角函数值)解直角三角形同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 21:20:27 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
4 解直角三角形
第2课时 已知边、角(或三角函数值)解直角三角形
认知基础练
练点1 已知斜边和一锐角 ( 或三角函数值)解直角三角形
1.在 Rt△ABC中,∠C=90°,若已知c,∠A,则下列各组式子中,能正确求出a,b的是( )
C. a=c·cosA,b=c·sinA D. a=c·sinA,b=c·cosA
2.在 Rt△ABC 中,∠C=90°,∠B=30°,AB=8,则BC 的长是( )
B.4
3.如图,在 Rt△ABC 中,∠ACB=90°,CD⊥AB 于点D,tan∠BCD= 则 BC 的长为_____________.
练点2 已知一直角边和一锐角(或三角函数值)解直角三角形
4.在 Rt△ABC中,∠C=90°,若a=6,∠B=45°,则b=___________,c=__________.
5.在 Rt△ABC中,∠C=90°, 的平分线 BD交AC 于点 D,若AD=16,则 BC 的长为( )
A.6 B.8 D.12
6.如图,在四边形 ABCD中,∠B=90°,AB=2,CD=8,连接AC,AC⊥CD,则 AD的长度是______________.
思维发散练
发散点1 利用解直角三角形求线段的长
7.如图,在 Rt△ABC中, 点 D在 BC上,且BD=AD.
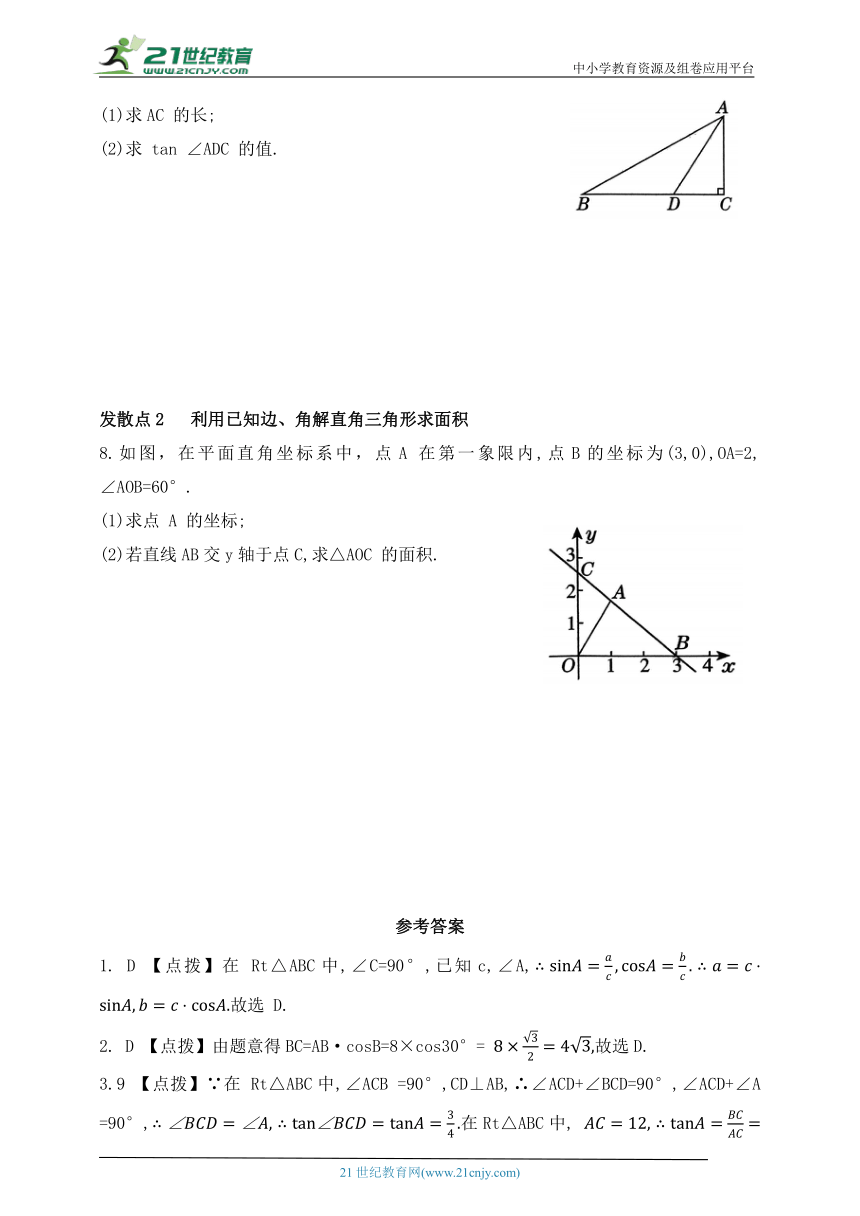
(1)求AC 的长;
(2)求 tan ∠ADC 的值.
发散点2 利用已知边、角解直角三角形求面积
8.如图,在平面直角坐标系中,点A 在第一象限内,点B的坐标为(3,0),OA=2, ∠AOB=60°.
(1)求点 A 的坐标;
(2)若直线AB交y轴于点C,求△AOC 的面积.
参考答案
1. D 【点拨】在 Rt△ABC中,∠C=90°,已知c,∠A,故选 D.
2. D 【点拨】由题意得BC=AB·cosB=8×cos30°= 故选D.
3.9 【点拨】∵在 Rt△ABC中,∠ACB =90°,CD⊥AB,∴∠ACD+∠BCD=90°,∠ACD+∠A =90°,在Rt△ABC中,
4.6;6 【点拨】∵∠C =90°,∠B=45°,∴∠A=45°,∴△ABC为等腰直角三角形,∴b=a=6,
5. C 【点拨】∵ ∠ABC=60°.
∵BD平分∠ABC,∴∠ABD=∠CBD=30°,∴∠A =∠ABD,∴ BD=AD= 16.
∵∠CBD= 故选C.
6.10 【点拨】在 Rt△ABC中,∵ AB=2,∴AC=6.
在 Rt△ACD中,∵AC=6,CD=8, 故答案为10.
7.【解】(1)∵在 Rt△ABC中,∠C = 90°,BC = 8,
(2)设 CD=x,则AD=BD=8-x.在 Rt△ACD中,根据勾股定理得AD =CD +AC ,即(8-x) =x +16,解得x=3,即 CD=3.
8.【解】(1)如图,过点A作AD⊥x轴,垂足为点 D.
在 Rt△OAD中,OA=2,∠AOB=60°,
∴点A的坐标是((1, ).
(2)设直线 AB对应的函数表达式为y=kx+b.
∵直线 AB过点 A(1, )和B(3,0), 解得
∴直线 AB 对应的函数表达式为
令x=0,则
点方法 过平面直角坐标系中的一点向x轴或向y轴作垂线是解决求点坐标及图形面积的主要方法.再在直角三角形中运用三角函数的知识,求出相关线段的长是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
4 解直角三角形
第2课时 已知边、角(或三角函数值)解直角三角形
认知基础练
练点1 已知斜边和一锐角 ( 或三角函数值)解直角三角形
1.在 Rt△ABC中,∠C=90°,若已知c,∠A,则下列各组式子中,能正确求出a,b的是( )
C. a=c·cosA,b=c·sinA D. a=c·sinA,b=c·cosA
2.在 Rt△ABC 中,∠C=90°,∠B=30°,AB=8,则BC 的长是( )
B.4
3.如图,在 Rt△ABC 中,∠ACB=90°,CD⊥AB 于点D,tan∠BCD= 则 BC 的长为_____________.
练点2 已知一直角边和一锐角(或三角函数值)解直角三角形
4.在 Rt△ABC中,∠C=90°,若a=6,∠B=45°,则b=___________,c=__________.
5.在 Rt△ABC中,∠C=90°, 的平分线 BD交AC 于点 D,若AD=16,则 BC 的长为( )
A.6 B.8 D.12
6.如图,在四边形 ABCD中,∠B=90°,AB=2,CD=8,连接AC,AC⊥CD,则 AD的长度是______________.
思维发散练
发散点1 利用解直角三角形求线段的长
7.如图,在 Rt△ABC中, 点 D在 BC上,且BD=AD.
(1)求AC 的长;
(2)求 tan ∠ADC 的值.
发散点2 利用已知边、角解直角三角形求面积
8.如图,在平面直角坐标系中,点A 在第一象限内,点B的坐标为(3,0),OA=2, ∠AOB=60°.
(1)求点 A 的坐标;
(2)若直线AB交y轴于点C,求△AOC 的面积.
参考答案
1. D 【点拨】在 Rt△ABC中,∠C=90°,已知c,∠A,故选 D.
2. D 【点拨】由题意得BC=AB·cosB=8×cos30°= 故选D.
3.9 【点拨】∵在 Rt△ABC中,∠ACB =90°,CD⊥AB,∴∠ACD+∠BCD=90°,∠ACD+∠A =90°,在Rt△ABC中,
4.6;6 【点拨】∵∠C =90°,∠B=45°,∴∠A=45°,∴△ABC为等腰直角三角形,∴b=a=6,
5. C 【点拨】∵ ∠ABC=60°.
∵BD平分∠ABC,∴∠ABD=∠CBD=30°,∴∠A =∠ABD,∴ BD=AD= 16.
∵∠CBD= 故选C.
6.10 【点拨】在 Rt△ABC中,∵ AB=2,∴AC=6.
在 Rt△ACD中,∵AC=6,CD=8, 故答案为10.
7.【解】(1)∵在 Rt△ABC中,∠C = 90°,BC = 8,
(2)设 CD=x,则AD=BD=8-x.在 Rt△ACD中,根据勾股定理得AD =CD +AC ,即(8-x) =x +16,解得x=3,即 CD=3.
8.【解】(1)如图,过点A作AD⊥x轴,垂足为点 D.
在 Rt△OAD中,OA=2,∠AOB=60°,
∴点A的坐标是((1, ).
(2)设直线 AB对应的函数表达式为y=kx+b.
∵直线 AB过点 A(1, )和B(3,0), 解得
∴直线 AB 对应的函数表达式为
令x=0,则
点方法 过平面直角坐标系中的一点向x轴或向y轴作垂线是解决求点坐标及图形面积的主要方法.再在直角三角形中运用三角函数的知识,求出相关线段的长是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
