2.5.2 利用解直角三角形解坡角问题同步练习(含解析)
文档属性
| 名称 | 2.5.2 利用解直角三角形解坡角问题同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 21:24:55 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
5 三角函数的应用
第2课时 利用解直角三角形解坡角问题
认知基础练
练点1 只含单一坡角的应用
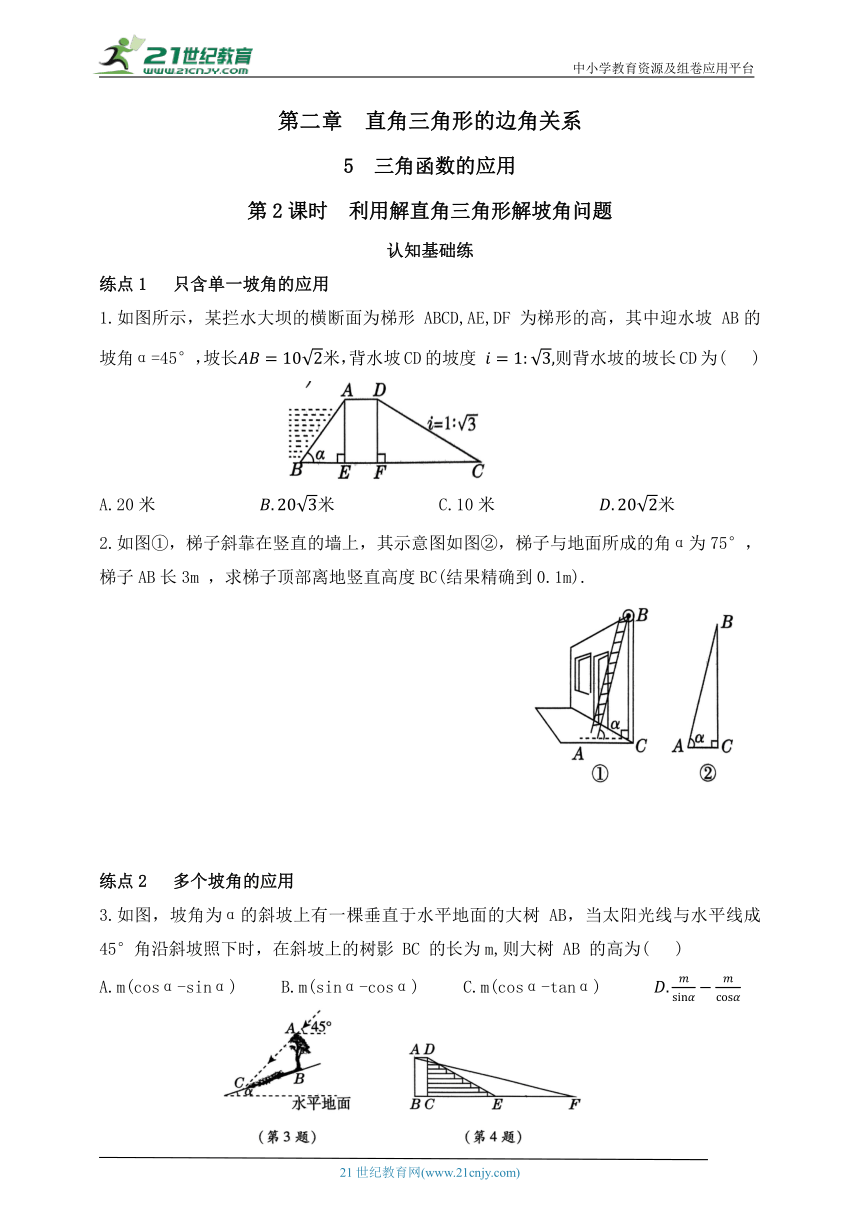
1.如图所示,某拦水大坝的横断面为梯形 ABCD,AE,DF 为梯形的高,其中迎水坡 AB的坡角α=45°,坡长米,背水坡CD的坡度 则背水坡的坡长CD为( )
A.20米 米 C.10米 米
2.如图①,梯子斜靠在竖直的墙上,其示意图如图②,梯子与地面所成的角α为75°,梯子AB长3m ,求梯子顶部离地竖直高度BC(结果精确到0.1m).
练点2 多个坡角的应用
3.如图,坡角为α的斜坡上有一棵垂直于水平地面的大树 AB,当太阳光线与水平线成45°角沿斜坡照下时,在斜坡上的树影 BC 的长为m,则大树 AB 的高为( )
A.m(cosα-sinα) B.m(sinα-cosα) C.m(cosα-tanα)
4.为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形ABCD为矩形,DE =10 m,其坡度为 将步梯 DE 改造为斜坡 AF,其坡度为i = 1:4,则斜坡 AF 的长度是______________m.(结果精确到0.01 m,参考数据:
思维发散练
发散点 利用坡角、视角测高
5.市政府为实现5G 网络全覆盖,2021~2025年拟建设5G基站三千个.如图,在斜坡 CB上有一建成的基站塔AB,斜坡 CB 的坡比为1:2.4.小芳在坡脚 C测得塔顶A的仰角为45°,然后她沿坡面 CB行走了 13米到达 D处,在D处测得塔顶A 的仰角为53°.(点A、B、C、D均在同一平面内,CE为地平线)(参考数据:
(1)求D处的竖直高度;
(2)求基站塔AB 的高.
参考答案
1. A 【点拨】∵迎水坡AB的坡角α=45°,坡长AB=米, (米),∴DF=AE = 10 米. ∵背水坡 CD的坡度
∴DC=2DF=20米,故选 A.
2.【解】在 Rt△ABC 中,AB=3m ,∠BAC=75°,
答:梯子顶部离地竖直高度 BC 约为 2.9 m.
3. A 【点拨】如图,过点 C作水平线与AB的延长线交于点 D,则AD⊥CD,∴∠BCD=α,∠ACD=45°.在 Rt△CDB 中,CD = m·cosα,BD = m·sinα,在 Rt△CDA 中,AD = CD×
tan45°=m×cosα×tan 45°=mcosα,∴AB=AD-BD=m·cosα-m·sinα=m(cosα-sinα).故选 A.
4.20. 62 【点拨】∵ DE 的坡度为
5m .∵四边形ABCD为矩形,∴ AB = CD = 5m .
∵斜坡AF的坡度为i =1:4,AB=5m ,∴BF=4AB=20 m,
在Rt△ABF中,20.62(m),
∴斜坡AF的长度约为20.62 m.
5.【解】(1)如图,过点 D作 DM⊥CE,垂足为M.
∵斜坡 CB的坡比为1:2.4,
设DM=5k米,则 CM=12k米,在 Rt△CDM 中,CD=13米,由勾股定理得CM +DM =CD , 即(12k) +(5k) =13 ,解得k=1(负值舍去),∴DM=5米,CM =12 米.
∴D处的竖直高度为5米.
(2)如图,延长AB交CE于点E,过点 D作DF⊥AE,垂足为点 F,则 DF=ME,DM=EF. 由斜坡 CB的坡度i=1:2.4,可设 DF=12a米,则 ME = 12a米,BF=5a米.
∵∠ACE=45°,∴∠CAE=∠ACE=45°,∴AE=CE=(12+12a)米,
∴AF=AE-EF=AE-DM=12+12a-5=(7+12a)米.
在 Rt△ADF中,∵DF=12a米,AF=(7+12a)米,∠ADF=53°,
解得
(米), (米),
(米).
答:基站塔AB的高为 米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
5 三角函数的应用
第2课时 利用解直角三角形解坡角问题
认知基础练
练点1 只含单一坡角的应用
1.如图所示,某拦水大坝的横断面为梯形 ABCD,AE,DF 为梯形的高,其中迎水坡 AB的坡角α=45°,坡长米,背水坡CD的坡度 则背水坡的坡长CD为( )
A.20米 米 C.10米 米
2.如图①,梯子斜靠在竖直的墙上,其示意图如图②,梯子与地面所成的角α为75°,梯子AB长3m ,求梯子顶部离地竖直高度BC(结果精确到0.1m).
练点2 多个坡角的应用
3.如图,坡角为α的斜坡上有一棵垂直于水平地面的大树 AB,当太阳光线与水平线成45°角沿斜坡照下时,在斜坡上的树影 BC 的长为m,则大树 AB 的高为( )
A.m(cosα-sinα) B.m(sinα-cosα) C.m(cosα-tanα)
4.为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形ABCD为矩形,DE =10 m,其坡度为 将步梯 DE 改造为斜坡 AF,其坡度为i = 1:4,则斜坡 AF 的长度是______________m.(结果精确到0.01 m,参考数据:
思维发散练
发散点 利用坡角、视角测高
5.市政府为实现5G 网络全覆盖,2021~2025年拟建设5G基站三千个.如图,在斜坡 CB上有一建成的基站塔AB,斜坡 CB 的坡比为1:2.4.小芳在坡脚 C测得塔顶A的仰角为45°,然后她沿坡面 CB行走了 13米到达 D处,在D处测得塔顶A 的仰角为53°.(点A、B、C、D均在同一平面内,CE为地平线)(参考数据:
(1)求D处的竖直高度;
(2)求基站塔AB 的高.
参考答案
1. A 【点拨】∵迎水坡AB的坡角α=45°,坡长AB=米, (米),∴DF=AE = 10 米. ∵背水坡 CD的坡度
∴DC=2DF=20米,故选 A.
2.【解】在 Rt△ABC 中,AB=3m ,∠BAC=75°,
答:梯子顶部离地竖直高度 BC 约为 2.9 m.
3. A 【点拨】如图,过点 C作水平线与AB的延长线交于点 D,则AD⊥CD,∴∠BCD=α,∠ACD=45°.在 Rt△CDB 中,CD = m·cosα,BD = m·sinα,在 Rt△CDA 中,AD = CD×
tan45°=m×cosα×tan 45°=mcosα,∴AB=AD-BD=m·cosα-m·sinα=m(cosα-sinα).故选 A.
4.20. 62 【点拨】∵ DE 的坡度为
5m .∵四边形ABCD为矩形,∴ AB = CD = 5m .
∵斜坡AF的坡度为i =1:4,AB=5m ,∴BF=4AB=20 m,
在Rt△ABF中,20.62(m),
∴斜坡AF的长度约为20.62 m.
5.【解】(1)如图,过点 D作 DM⊥CE,垂足为M.
∵斜坡 CB的坡比为1:2.4,
设DM=5k米,则 CM=12k米,在 Rt△CDM 中,CD=13米,由勾股定理得CM +DM =CD , 即(12k) +(5k) =13 ,解得k=1(负值舍去),∴DM=5米,CM =12 米.
∴D处的竖直高度为5米.
(2)如图,延长AB交CE于点E,过点 D作DF⊥AE,垂足为点 F,则 DF=ME,DM=EF. 由斜坡 CB的坡度i=1:2.4,可设 DF=12a米,则 ME = 12a米,BF=5a米.
∵∠ACE=45°,∴∠CAE=∠ACE=45°,∴AE=CE=(12+12a)米,
∴AF=AE-EF=AE-DM=12+12a-5=(7+12a)米.
在 Rt△ADF中,∵DF=12a米,AF=(7+12a)米,∠ADF=53°,
解得
(米), (米),
(米).
答:基站塔AB的高为 米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
