2.6 利用三角函数测高同步练习(含解析)
文档属性
| 名称 | 2.6 利用三角函数测高同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
6 利用三角函数测高
认知基础练
活动1 测量底部可以到达的物体高度
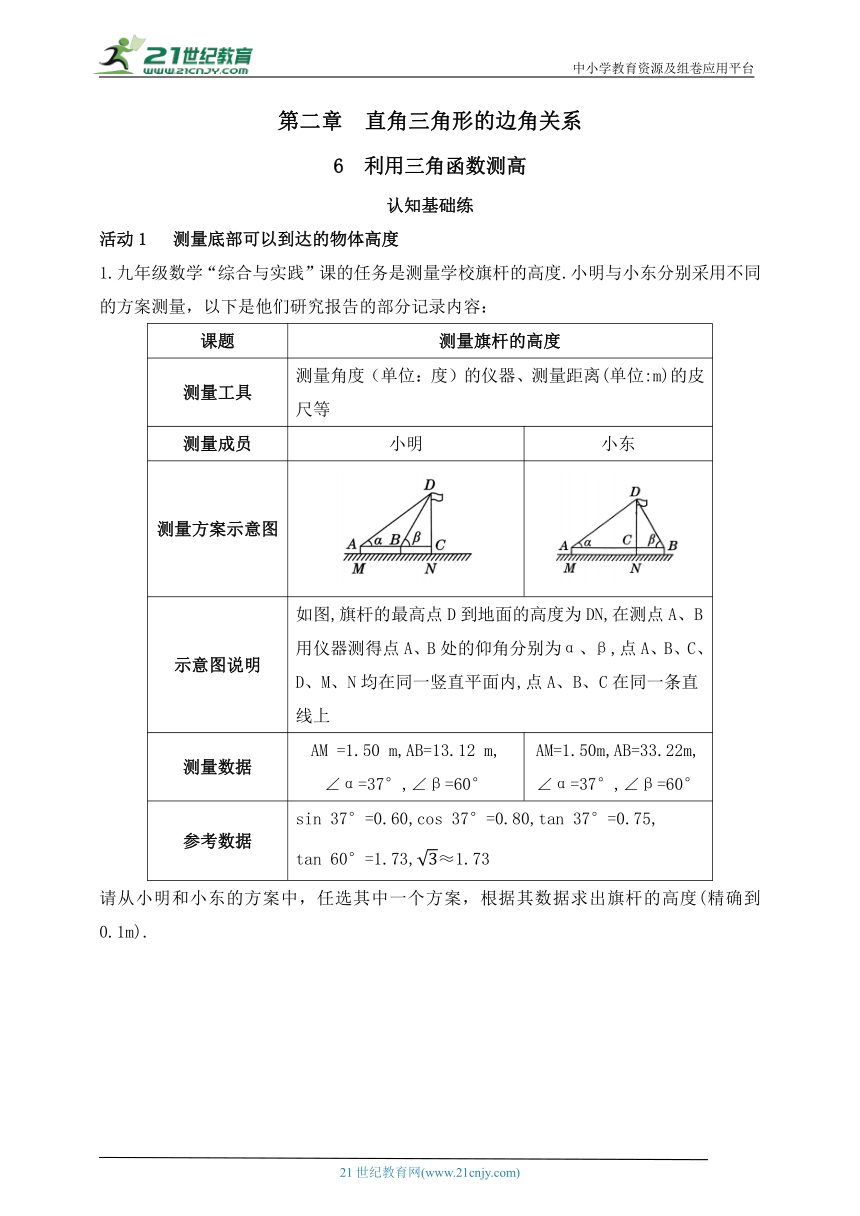
1.九年级数学“综合与实践”课的任务是测量学校旗杆的高度.小明与小东分别采用不同的方案测量,以下是他们研究报告的部分记录内容:
课题 测量旗杆的高度
测量工具 测量角度(单位:度)的仪器、测量距离(单位:m)的皮尺等
测量成员 小明 小东
测量方案示意图
示意图说明 如图,旗杆的最高点D到地面的高度为DN,在测点A、B用仪器测得点A、B处的仰角分别为α、β,点A、B、C、D、M、N均在同一竖直平面内,点A、B、C在同一条直线上
测量数据 AM =1.50 m,AB=13.12 m, ∠α=37°,∠β=60° AM=1.50m,AB=33.22m,∠α=37°,∠β=60°
参考数据 sin 37°=0.60,cos 37°=0.80,tan 37°=0.75, tan 60°=1.73,≈1.73
请从小明和小东的方案中,任选其中一个方案,根据其数据求出旗杆的高度(精确到0.1m).
活动2 测量底部不可到达的物体高度
2.学科素养模型观念为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,如图,他们在河南岸的点 A 处测得河北岸的树H恰好在A 的正北方向,测量方案与数据如下表:
课题 测量河流宽度
测量工具 测量角度的仪器、皮尺等
测量小组 第一小组 第二小组 第三小组
测量方案示意图
说明 点B,C在点A 的正东方向 点B,D在点A 的正东方向 点B在点A的正东方向,点C在点A的正西方向
测量数据 BC=60m, ∠ABH=70°, ∠ACH=35° BD=20m, ∠ABH=70°, ∠BCD=35° BC=101m, ∠ABH=70°, ∠ACH =35°
(1)哪个小组的数据无法计算出河宽
(2)请选择其中一个方案及其数据求出河宽(精确到 0.1m ).
(参考数据:sin 70°≈0.94, sin 35°≈0.57, tan 70°≈2.75, tan 35°≈0.70)
参考答案
1.【解】选小明的方案.设DC=xm,则由题意,得BC=
解得x≈17.37,
则旗杆的高度 DN=DC+CN≈17.37+1.50≈18.9(m).
选小东的方案.设DC=xm,则由题意得
解得 x≈17.38,
则旗杆的高度 DN = DC + CN≈17.38 +1.50≈18.9(m).
2.【解】(1)第二小组的数据无法计算出河宽.
(2)第一小组:
∵∠ABH=∠ACH+∠BHC,∠ABH=70°,∠ACH=35°,∴∠BHC=∠BCH=35°.∴BC = BH=60 m.
∴AH=BH·sin∠ABH=BH·sin 70°≈60×0. 94=56.4(m).
第三小组:设 AH =xm,则
解得x≈56.4.
答:河宽约为 56.4m .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
6 利用三角函数测高
认知基础练
活动1 测量底部可以到达的物体高度
1.九年级数学“综合与实践”课的任务是测量学校旗杆的高度.小明与小东分别采用不同的方案测量,以下是他们研究报告的部分记录内容:
课题 测量旗杆的高度
测量工具 测量角度(单位:度)的仪器、测量距离(单位:m)的皮尺等
测量成员 小明 小东
测量方案示意图
示意图说明 如图,旗杆的最高点D到地面的高度为DN,在测点A、B用仪器测得点A、B处的仰角分别为α、β,点A、B、C、D、M、N均在同一竖直平面内,点A、B、C在同一条直线上
测量数据 AM =1.50 m,AB=13.12 m, ∠α=37°,∠β=60° AM=1.50m,AB=33.22m,∠α=37°,∠β=60°
参考数据 sin 37°=0.60,cos 37°=0.80,tan 37°=0.75, tan 60°=1.73,≈1.73
请从小明和小东的方案中,任选其中一个方案,根据其数据求出旗杆的高度(精确到0.1m).
活动2 测量底部不可到达的物体高度
2.学科素养模型观念为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,如图,他们在河南岸的点 A 处测得河北岸的树H恰好在A 的正北方向,测量方案与数据如下表:
课题 测量河流宽度
测量工具 测量角度的仪器、皮尺等
测量小组 第一小组 第二小组 第三小组
测量方案示意图
说明 点B,C在点A 的正东方向 点B,D在点A 的正东方向 点B在点A的正东方向,点C在点A的正西方向
测量数据 BC=60m, ∠ABH=70°, ∠ACH=35° BD=20m, ∠ABH=70°, ∠BCD=35° BC=101m, ∠ABH=70°, ∠ACH =35°
(1)哪个小组的数据无法计算出河宽
(2)请选择其中一个方案及其数据求出河宽(精确到 0.1m ).
(参考数据:sin 70°≈0.94, sin 35°≈0.57, tan 70°≈2.75, tan 35°≈0.70)
参考答案
1.【解】选小明的方案.设DC=xm,则由题意,得BC=
解得x≈17.37,
则旗杆的高度 DN=DC+CN≈17.37+1.50≈18.9(m).
选小东的方案.设DC=xm,则由题意得
解得 x≈17.38,
则旗杆的高度 DN = DC + CN≈17.38 +1.50≈18.9(m).
2.【解】(1)第二小组的数据无法计算出河宽.
(2)第一小组:
∵∠ABH=∠ACH+∠BHC,∠ABH=70°,∠ACH=35°,∴∠BHC=∠BCH=35°.∴BC = BH=60 m.
∴AH=BH·sin∠ABH=BH·sin 70°≈60×0. 94=56.4(m).
第三小组:设 AH =xm,则
解得x≈56.4.
答:河宽约为 56.4m .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
