第二章 直角三角形的边角关系专题 求锐角三角函数值的七种常见方法同步练习(含解析)
文档属性
| 名称 | 第二章 直角三角形的边角关系专题 求锐角三角函数值的七种常见方法同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 21:29:03 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
专题 求锐角三角函数值的七种常见方法
方法1 定义法
1.在Rt△ACB中,∠C=则 BC的长为( )
A.6 B.7.5 C.8 D.12.5
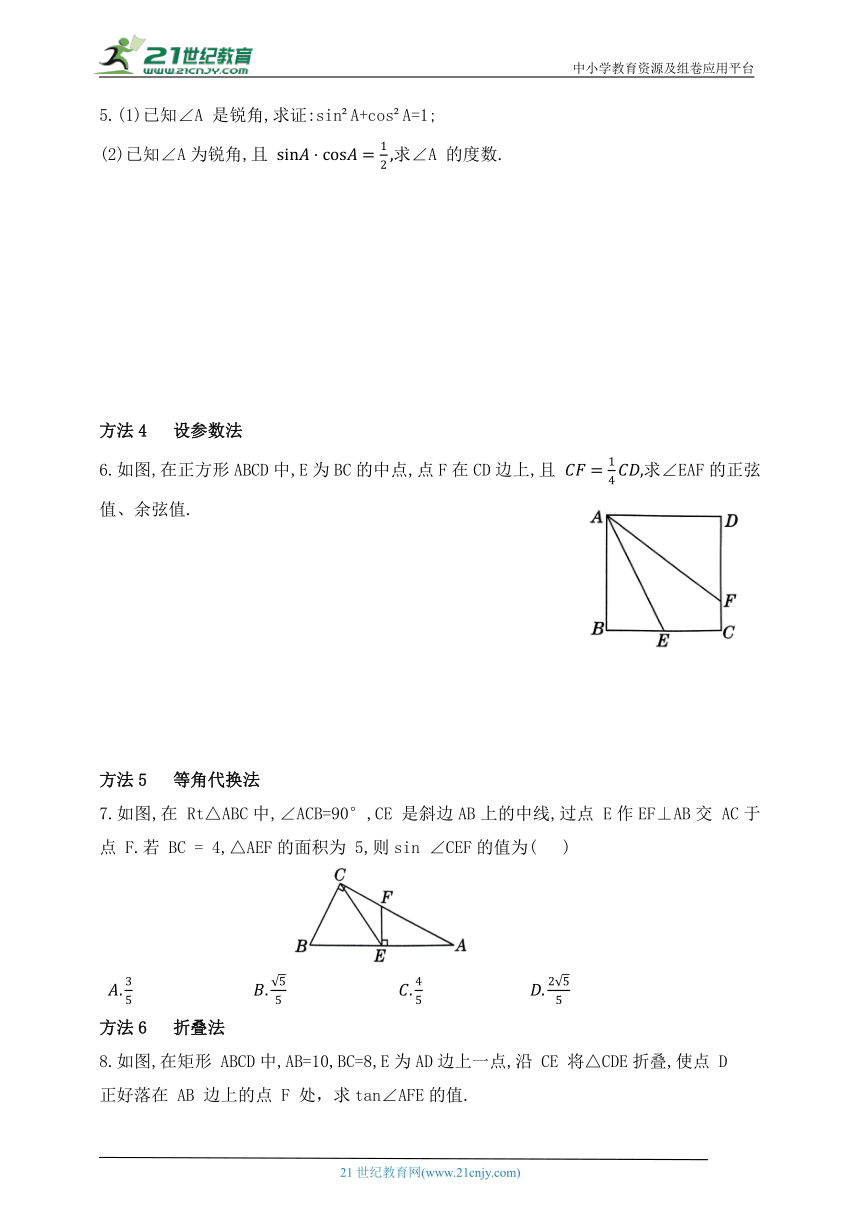
2.中国古代数学家赵爽在为《周髀算经》作注解时,用4个全等的直角三角形拼成正方形(如图),并用它证明了勾股定理,这个图被称为“弦图”.若“弦图”中小正方形面积与每个直角三角形面积均为1,α为直角三角形中的一个锐角,则 tanα=( )
A.2 C.
方法2 特殊角法
3.北京冬奥会开幕式的巨型雪花状主火炬塔的设计,体现了环保低碳理念. 如图所示,它的主体形状呈正六边形.若点A,F,B,D,C,E是正六边 形 的六个顶点,则 tan∠ABE=____________.
方法3 同角或互余角法
4.如图,在△ABC 中,∠ACB = 90°,CD⊥AB于D,若 则tan∠BCD的值为( )
5.(1)已知∠A 是锐角,求证:sin A+cos A=1;
(2)已知∠A为锐角,且 求∠A 的度数.
方法4 设参数法
6.如图,在正方形ABCD中,E为BC的中点,点F在CD边上,且 求∠EAF的正弦值、余弦值.
方法5 等角代换法
7.如图,在 Rt△ABC中,∠ACB=90°,CE 是斜边AB上的中线,过点 E作EF⊥AB交 AC于点 F.若 BC = 4,△AEF的面积为 5,则sin ∠CEF的值为( )
方法6 折叠法
8.如图,在矩形 ABCD中,AB=10,BC=8,E为AD边上一点,沿 CE 将△CDE折叠,使点 D
正好落在 AB 边上的点 F 处,求tan∠AFE的值.
方法7 网格构造直角法
9.如图,在4×4正方形网格中,每个小正方形的边长均为1,点A,B,C,E为网格交点,AD⊥BC,垂足为 D,则sin∠BAD的值为( )
10.问题呈现
如图①,在边长为1的正方形网格中,连接格点 D,N和 E,C,DN与EC 相交于点 P,求 tan∠CPN的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形,观察发现,问题中∠CPN不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比
如连接格点 M,N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中.
问题解决
(1)图①中 tan∠CPN的值为______________;
(2)如图②,在边长为1 的正方形网格中,AN与CM 相交于点 P,求 cos∠CPN的值.
思维拓展
(3)如图③,AB⊥BC,AB=4BC,点 M在AB上,且AM=BC,延长CB到 N,使 BN=2BC,连接AN交CM 的延长线于点 P,用上述方法构造网格求∠CPN的度数.
参考答案
练素养
1. A 【点拨】∵ 故选A.
2. A 【点拨】由已知可得,大正方形的面积为1×4+1=5.设直角三角形的长直角边为a,短直角边为b,则 解得 或 (不合题意,舍去).
【点拨】连接AB、BC、AC、BE.∵点A,F,B,D,C,E是正六边形的六个顶点,∴AB = BC =AC,BE垂直平分AC,∴△ABC 是等边三角形,∴∠ABC= 故答案为
4. B 【点拨】由勾股定理知, .根据同角的余角相等,得∠BCD=∠A.∴tan∠BCD= 故选 B.
5.(1)【证明】设△ABC 中,∠C=90°,∠A,∠B,∠C的对边分别为 a,b,c,则 根据勾股定理,得a +b =c ,
(2)【解】设 sin A=x(x>0),则sin A =x ,cos A=1-x .
即4x -4x +1=0.
∴(2x -1) =0.∴2x -1=0,即 (负值已舍去),即
6.【解】连接 EF,设CF=k.则CD=AD=AB=BC=4k,∴BE=EC=2k,DF=3k.
根据勾股定理,得 ∴EF +AE =25k =AF .
∴△AEF是直角三角形,且∠AEF=90°.
点方法 当出现边与边的比时,可引入参数,用这个参数表示三角形三边长,再用定义求解.
7. A 【点拨】连接BF.∵ CE是斜边AB上的中线,EF⊥AB,∴EF是 AB的垂直平分线.
∴ AF= BF,
在 Rt△BCF中.
由题易得 又∵∠BCA=90°=∠BEF, ∴∠CBF=90°-∠BFC=90°-2∠A,∠CEF = 90°-∠BEC = 90°-2∠A.
8.【解】∵四边形ABCD 是矩形,∴∠D=∠B=90°.
根据图形得∠AFE+∠EFC+∠BFC=180°.
根据折叠的性质,知∠EFC=∠D=90°,∴∠AFE+∠BFC=90°.
∵在 Rt△BCF中,∠BCF+∠BFC=90°,∴∠AFE=∠BCF.
根据折叠的性质,得CF=CD=10.
在 Rt△BFC中,BC=8,CF=10,
9. C 【点拨】在 Rt△BEC 中,
∵∠ABD+∠CBE = 90°,∴∠BAD = ∠CBE, 故选 C.
10.【解】(1)2
(2)如图①,取格点 B,连接AB,可得AB∥MC,∴∠CPN=∠BAN.
连接BN,易知△ABN为直角三角形.
在Rt△ABN中,.
(3)设 BC 的长为单位1,构造如图②所示的网格,取格点 D,连接AD,可得AD∥CM,
∴∠CPN=∠DAN.连接DN,易知△ADN为直角三角形.
在Rt△ADN中,
∴∠CPN=45°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
专题 求锐角三角函数值的七种常见方法
方法1 定义法
1.在Rt△ACB中,∠C=则 BC的长为( )
A.6 B.7.5 C.8 D.12.5
2.中国古代数学家赵爽在为《周髀算经》作注解时,用4个全等的直角三角形拼成正方形(如图),并用它证明了勾股定理,这个图被称为“弦图”.若“弦图”中小正方形面积与每个直角三角形面积均为1,α为直角三角形中的一个锐角,则 tanα=( )
A.2 C.
方法2 特殊角法
3.北京冬奥会开幕式的巨型雪花状主火炬塔的设计,体现了环保低碳理念. 如图所示,它的主体形状呈正六边形.若点A,F,B,D,C,E是正六边 形 的六个顶点,则 tan∠ABE=____________.
方法3 同角或互余角法
4.如图,在△ABC 中,∠ACB = 90°,CD⊥AB于D,若 则tan∠BCD的值为( )
5.(1)已知∠A 是锐角,求证:sin A+cos A=1;
(2)已知∠A为锐角,且 求∠A 的度数.
方法4 设参数法
6.如图,在正方形ABCD中,E为BC的中点,点F在CD边上,且 求∠EAF的正弦值、余弦值.
方法5 等角代换法
7.如图,在 Rt△ABC中,∠ACB=90°,CE 是斜边AB上的中线,过点 E作EF⊥AB交 AC于点 F.若 BC = 4,△AEF的面积为 5,则sin ∠CEF的值为( )
方法6 折叠法
8.如图,在矩形 ABCD中,AB=10,BC=8,E为AD边上一点,沿 CE 将△CDE折叠,使点 D
正好落在 AB 边上的点 F 处,求tan∠AFE的值.
方法7 网格构造直角法
9.如图,在4×4正方形网格中,每个小正方形的边长均为1,点A,B,C,E为网格交点,AD⊥BC,垂足为 D,则sin∠BAD的值为( )
10.问题呈现
如图①,在边长为1的正方形网格中,连接格点 D,N和 E,C,DN与EC 相交于点 P,求 tan∠CPN的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形,观察发现,问题中∠CPN不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比
如连接格点 M,N,可得MN∥EC,则∠DNM=∠CPN,连接DM,那么∠CPN就变换到Rt△DMN中.
问题解决
(1)图①中 tan∠CPN的值为______________;
(2)如图②,在边长为1 的正方形网格中,AN与CM 相交于点 P,求 cos∠CPN的值.
思维拓展
(3)如图③,AB⊥BC,AB=4BC,点 M在AB上,且AM=BC,延长CB到 N,使 BN=2BC,连接AN交CM 的延长线于点 P,用上述方法构造网格求∠CPN的度数.
参考答案
练素养
1. A 【点拨】∵ 故选A.
2. A 【点拨】由已知可得,大正方形的面积为1×4+1=5.设直角三角形的长直角边为a,短直角边为b,则 解得 或 (不合题意,舍去).
【点拨】连接AB、BC、AC、BE.∵点A,F,B,D,C,E是正六边形的六个顶点,∴AB = BC =AC,BE垂直平分AC,∴△ABC 是等边三角形,∴∠ABC= 故答案为
4. B 【点拨】由勾股定理知, .根据同角的余角相等,得∠BCD=∠A.∴tan∠BCD= 故选 B.
5.(1)【证明】设△ABC 中,∠C=90°,∠A,∠B,∠C的对边分别为 a,b,c,则 根据勾股定理,得a +b =c ,
(2)【解】设 sin A=x(x>0),则sin A =x ,cos A=1-x .
即4x -4x +1=0.
∴(2x -1) =0.∴2x -1=0,即 (负值已舍去),即
6.【解】连接 EF,设CF=k.则CD=AD=AB=BC=4k,∴BE=EC=2k,DF=3k.
根据勾股定理,得 ∴EF +AE =25k =AF .
∴△AEF是直角三角形,且∠AEF=90°.
点方法 当出现边与边的比时,可引入参数,用这个参数表示三角形三边长,再用定义求解.
7. A 【点拨】连接BF.∵ CE是斜边AB上的中线,EF⊥AB,∴EF是 AB的垂直平分线.
∴ AF= BF,
在 Rt△BCF中.
由题易得 又∵∠BCA=90°=∠BEF, ∴∠CBF=90°-∠BFC=90°-2∠A,∠CEF = 90°-∠BEC = 90°-2∠A.
8.【解】∵四边形ABCD 是矩形,∴∠D=∠B=90°.
根据图形得∠AFE+∠EFC+∠BFC=180°.
根据折叠的性质,知∠EFC=∠D=90°,∴∠AFE+∠BFC=90°.
∵在 Rt△BCF中,∠BCF+∠BFC=90°,∴∠AFE=∠BCF.
根据折叠的性质,得CF=CD=10.
在 Rt△BFC中,BC=8,CF=10,
9. C 【点拨】在 Rt△BEC 中,
∵∠ABD+∠CBE = 90°,∴∠BAD = ∠CBE, 故选 C.
10.【解】(1)2
(2)如图①,取格点 B,连接AB,可得AB∥MC,∴∠CPN=∠BAN.
连接BN,易知△ABN为直角三角形.
在Rt△ABN中,.
(3)设 BC 的长为单位1,构造如图②所示的网格,取格点 D,连接AD,可得AD∥CM,
∴∠CPN=∠DAN.连接DN,易知△ADN为直角三角形.
在Rt△ADN中,
∴∠CPN=45°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
