第二章 直角三角形的边角关系专题 解直角三角形的六种常见类型同步练习(含解析)
文档属性
| 名称 | 第二章 直角三角形的边角关系专题 解直角三角形的六种常见类型同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 21:30:11 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
专题 解直角三角形的六种常见类型
类型1 已知两直角边解直角三角形
1.如图,在 Rt△ABC 中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,求这个三角形的其他元素.
类型2 已知一直角边和斜边解直角三角形
2.如图,∠ACB=90°,AB=13,AC=12,∠BCM=∠BAC,求 sin ∠BAC 的值和点 B到直线 MC 的距离.
类型3 已知一直角边和一锐角解直角三角形
3.如图,在 Rt△ABC中,∠C=90°,∠A =30°,BC =3,D为AC边上一点,∠BDC=45°,求
AD 的长.
类型4 已知斜边和一锐角解直角三角形
4.如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,与BC 相交于点 D,且AB = ,求AD 的长.
类型5 已知一边和一锐角的函数值解直角三角形
5.如图,已知△ABD中,AC⊥BD,BC =8,CD=BF为AD边上的中线.
(1)求AC 的长;
(2)求 tan∠FBD的值.
类型6 已知非直角三角形中的边(或角或三角函数值) 解直角三角形
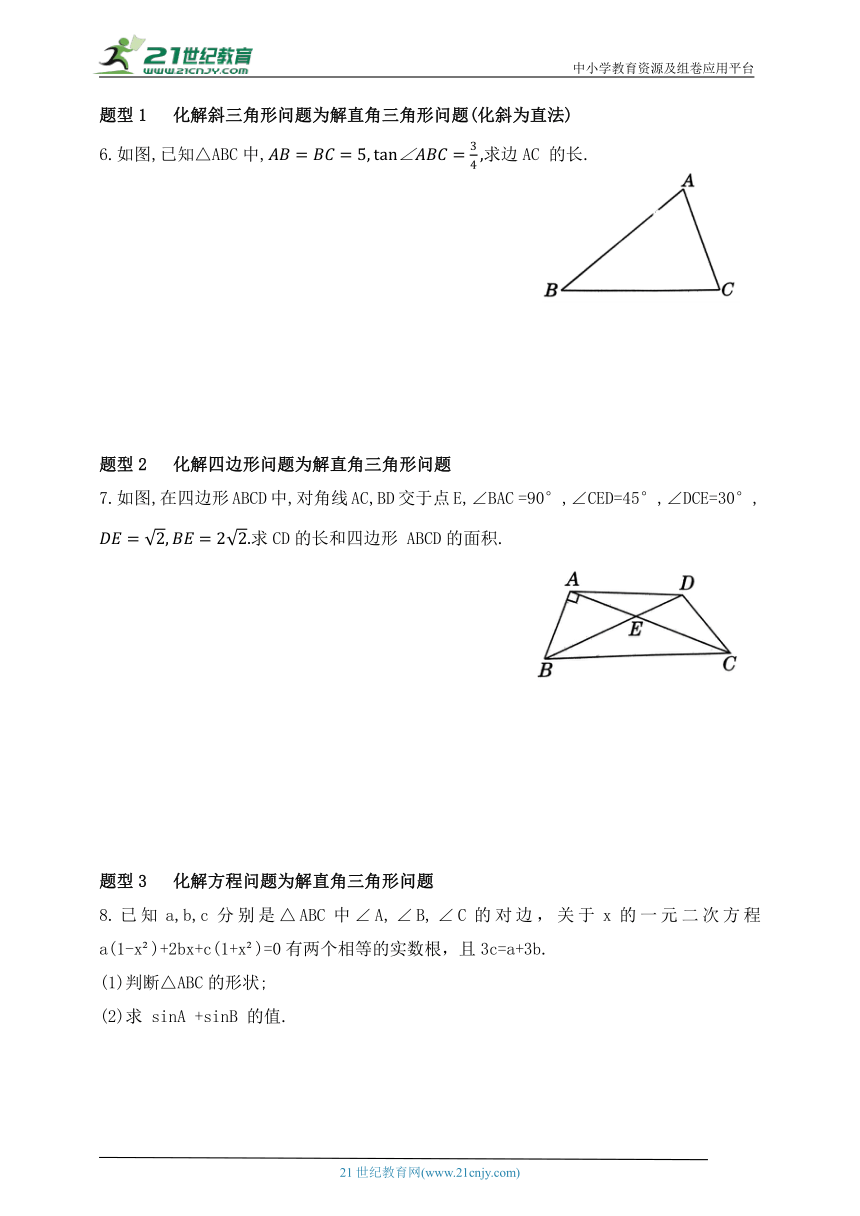
题型1 化解斜三角形问题为解直角三角形问题(化斜为直法)
6.如图,已知△ABC中,求边AC 的长.
题型2 化解四边形问题为解直角三角形问题
7.如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC =90°,∠CED=45°,∠DCE=30°,
求CD的长和四边形 ABCD的面积.
题型3 化解方程问题为解直角三角形问题
8.已知a,b,c分别是△ABC中∠A,∠B,∠C的对边,关于x的一元二次方程 a(1-x )+2bx+c(1+x )=0有两个相等的实数根,且3c=a+3b.
(1)判断△ABC的形状;
(2)求 sinA +sinB 的值.
参考答案
1.【解】
∴∠A=30°.∴∠B=90°-∠A=90°-30°=60°.
2.【解】∵AB=13,AC=12,∠ACB=90°,
过点 B作 BD⊥MC 于点 D.
∵∠BCM=∠BAC,∴sin ∠BCM= sin ∠BAC.即
即点 B到直线 MC 的距离为
3.【解】∵∠C=90°,∠BDC=45°,BC=3,∴CD=3.
4.【解】∵
又∵AD是∠BAC的平分线,∴∠CAD=30°.
5.【解】
(2)如图,连接 CF,过点 F作FE⊥BD,垂足为点 E.
∵BF为AD边上的中线,即F为AD的中点,
在 Rt△ACD中,由勾股定理得
在Rt△EFC中,
6.【解】过点 A作AE⊥BC于点E,
在 Rt△ABE中,∴AE=3,BE=4,∴CE=BC-BE=5-4=1,
在 Rt△AEC中,根据勾股定理,得
7.【解】如图,过点 D作 DH⊥AC 于点 H.
∵∠CED=45°,
又∵∠DCE=30°,
∴AB=AE=2.
8.【解】(1)整理方程得((c-a)x +2bx+(a+c)=0,则△=(2b) -4(c-a)(a+c)=4(b +a -c ).
∵方程有两个相等的实数根,∴△=0,即b +a =c .
∴△ABC为直角三角形,且∠C=90°.
(2)由3c=a+3b,得a=3c-3b.①
将①代入a +b =c ,得(3c-3b) +b =c .
∴4c -9bc+5b =0,即(4c-5b)(c-b)=0.
由①可知
将②代入①,得
∴在Rt△ABC中,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
专题 解直角三角形的六种常见类型
类型1 已知两直角边解直角三角形
1.如图,在 Rt△ABC 中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,求这个三角形的其他元素.
类型2 已知一直角边和斜边解直角三角形
2.如图,∠ACB=90°,AB=13,AC=12,∠BCM=∠BAC,求 sin ∠BAC 的值和点 B到直线 MC 的距离.
类型3 已知一直角边和一锐角解直角三角形
3.如图,在 Rt△ABC中,∠C=90°,∠A =30°,BC =3,D为AC边上一点,∠BDC=45°,求
AD 的长.
类型4 已知斜边和一锐角解直角三角形
4.如图,在△ABC中,∠C=90°,∠B=30°,AD是∠BAC的平分线,与BC 相交于点 D,且AB = ,求AD 的长.
类型5 已知一边和一锐角的函数值解直角三角形
5.如图,已知△ABD中,AC⊥BD,BC =8,CD=BF为AD边上的中线.
(1)求AC 的长;
(2)求 tan∠FBD的值.
类型6 已知非直角三角形中的边(或角或三角函数值) 解直角三角形
题型1 化解斜三角形问题为解直角三角形问题(化斜为直法)
6.如图,已知△ABC中,求边AC 的长.
题型2 化解四边形问题为解直角三角形问题
7.如图,在四边形ABCD中,对角线AC,BD交于点E,∠BAC =90°,∠CED=45°,∠DCE=30°,
求CD的长和四边形 ABCD的面积.
题型3 化解方程问题为解直角三角形问题
8.已知a,b,c分别是△ABC中∠A,∠B,∠C的对边,关于x的一元二次方程 a(1-x )+2bx+c(1+x )=0有两个相等的实数根,且3c=a+3b.
(1)判断△ABC的形状;
(2)求 sinA +sinB 的值.
参考答案
1.【解】
∴∠A=30°.∴∠B=90°-∠A=90°-30°=60°.
2.【解】∵AB=13,AC=12,∠ACB=90°,
过点 B作 BD⊥MC 于点 D.
∵∠BCM=∠BAC,∴sin ∠BCM= sin ∠BAC.即
即点 B到直线 MC 的距离为
3.【解】∵∠C=90°,∠BDC=45°,BC=3,∴CD=3.
4.【解】∵
又∵AD是∠BAC的平分线,∴∠CAD=30°.
5.【解】
(2)如图,连接 CF,过点 F作FE⊥BD,垂足为点 E.
∵BF为AD边上的中线,即F为AD的中点,
在 Rt△ACD中,由勾股定理得
在Rt△EFC中,
6.【解】过点 A作AE⊥BC于点E,
在 Rt△ABE中,∴AE=3,BE=4,∴CE=BC-BE=5-4=1,
在 Rt△AEC中,根据勾股定理,得
7.【解】如图,过点 D作 DH⊥AC 于点 H.
∵∠CED=45°,
又∵∠DCE=30°,
∴AB=AE=2.
8.【解】(1)整理方程得((c-a)x +2bx+(a+c)=0,则△=(2b) -4(c-a)(a+c)=4(b +a -c ).
∵方程有两个相等的实数根,∴△=0,即b +a =c .
∴△ABC为直角三角形,且∠C=90°.
(2)由3c=a+3b,得a=3c-3b.①
将①代入a +b =c ,得(3c-3b) +b =c .
∴4c -9bc+5b =0,即(4c-5b)(c-b)=0.
由①可知
将②代入①,得
∴在Rt△ABC中,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
