第二章 直角三角形的边角关系专题 锐角三角函数的计算同步练习(含解析)
文档属性
| 名称 | 第二章 直角三角形的边角关系专题 锐角三角函数的计算同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 21:31:41 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
专题 锐角三角函数的计算
一、选择题(每题4分,共32分)
1.下列计算结果正确的是( )
A.(a ) =a
2.在△ABC中,∠C=90°,BC=6,AC=8,则 sin A 的值为( )
3.在正方形网格中,△ABC 的位置如图所示,点A,B,C均在格点上,则 sin∠BAC的值为( )
4.在△ABC 中,∠C =90°,则AC 等于( )
A.3 B.2 C. D.
5.如图,已知点 P(4,3),OP与x轴正半轴的夹角为α,则 cosα=( )
6.如图,以O为圆心,任意长为半径画弧,与射线OA 交于点 B,再以B为圆心,BO 长为半径画弧,两弧交于点 C,画射线OC,则 tan∠AOC的值为( )
D.
7.在△ABC中,∠A、∠B均为锐角,且 则△ABC是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
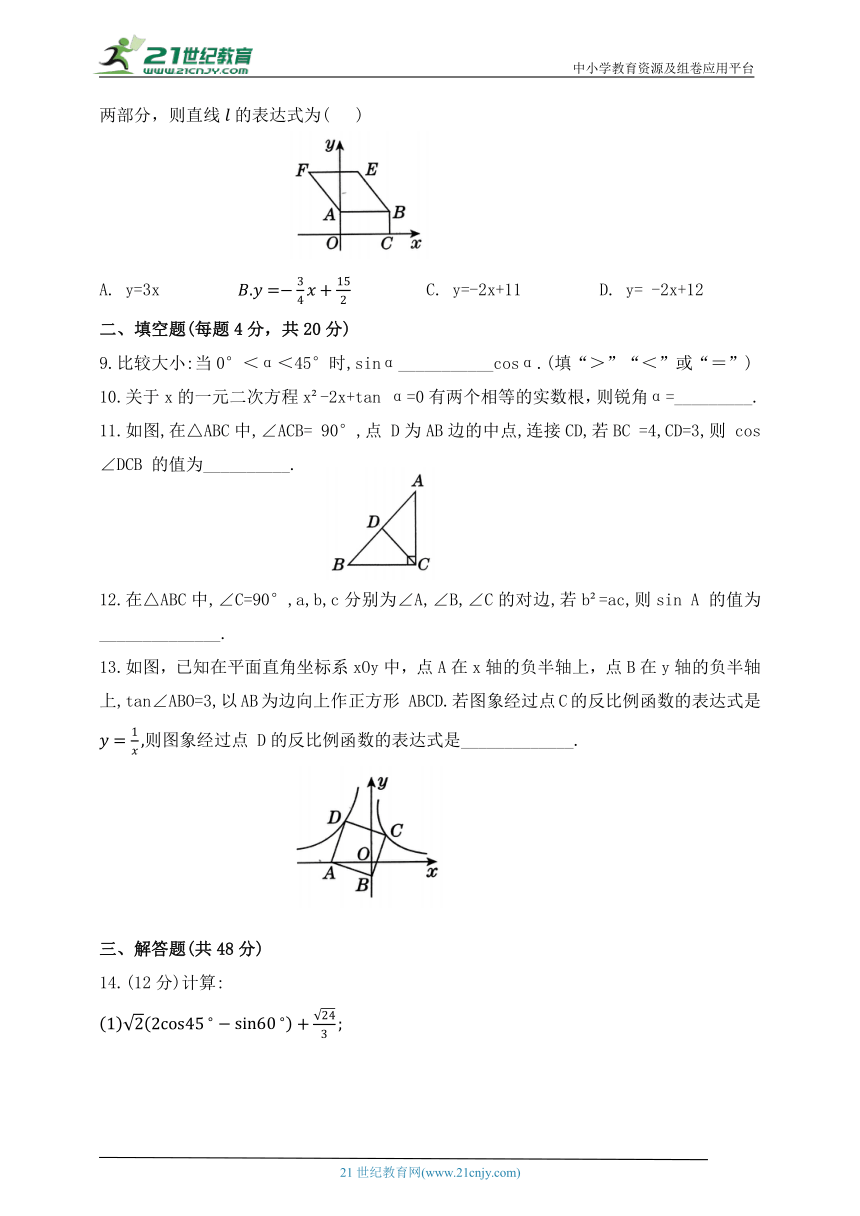
8.如图,在平面直角坐标系xOy中,矩形 OABC 的顶点 B的坐标为(10,4),四边形ABEF是菱形,且 若直线把矩形OABC 和菱形ABEF组成的图形的面积分成相等的两部分,则直线的表达式为( )
A. y=3x C. y=-2x+11 D. y= -2x+12
二、填空题(每题4分,共20分)
9.比较大小:当0°<α<45°时,sinα___________cosα.(填“>”“<”或“=”)
10.关于x的一元二次方程x -2x+tan α=0有两个相等的实数根,则锐角α=_________.
11.如图,在△ABC中,∠ACB= 90°,点 D为AB边的中点,连接CD,若BC =4,CD=3,则 cos∠DCB 的值为__________.
12.在△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,若b =ac,则sin A 的值为______________.
13.如图,已知在平面直角坐标系xOy中,点A在x轴的负半轴上,点B在y轴的负半轴上,tan∠ABO=3,以AB为边向上作正方形 ABCD.若图象经过点C的反比例函数的表达式是 则图象经过点 D的反比例函数的表达式是_____________.
三、解答题(共48分)
14.(12分)计算:
(2)(-2) -3tan 30°+|tan 60°-2|.
15.(10分)如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,求AC的长和 sin A 的值.
16.(12分)吉林省广播电视塔(简称“吉塔”)是吉林省省会长春市的标志性建筑之一.某科技兴趣小组利用无人机搭载测量仪器测量“吉塔”的高度,如图,将无人机置于距离“吉塔”138米的点 C 处.从无人机上观测塔尖A的仰角为30°,观测塔基座中心点 B 的俯角为45°.求“吉塔”的高度(结果保留整数,参考数据:
17.(14分)知识再现
如图①,在 Rt△ABC中,∠C= 90°,∠A,∠B,∠C的对边分别为a,b,c.
拓展探究
如图②,在锐角三角形 ABC中,∠A,∠B,∠C的对边分别为a,b,c.
请探究 之间的关系,并写出探究过程.
解决问题
如图③,为测量点A到河对岸点 B的距离,选取与点A 在河岸同一侧的点 C,测得AC=
60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点 A到点 B的距离.
参考答案
一、1. C 【点拨】 故选 C.
2. C 【点拨】由勾股定理得AB=10,再根据三角函数定义得 故本题选 C.
3. A 【点拨】设小正方形的边长为1,作CD⊥AB交AB 的延长线于点 D.∵在 Rt△ACD中,∠ADC= 故选A.
4. B 【点拨】 故选 B.
5. B 【点拨】过P作PN⊥x轴于N.∵P(4,3),∴ON=4,PN=3,∴在 Rt△PON中,由勾股定理得 OP = 故选B.
6. D 【点拨】如图,连接BC,则由题意可得OC=OB,CB=OB,∴OC= OB=BC,∴△BOC是等边三角形,∴∠AOC= 故选D.
7. B【点拨】∵ 在△ABC中,∠C=180°-60°-60°=60°,∴△ABC是等边三角形.故选 B.
8. D 【点拨】连接OB,AC,交于点M;连接AE,BF,交于点N,过M、N两点作直线,则直线MN为符合条件的直线l,如图所示.∵四边形 OABC 是矩形,∴OM = BM.∵点 B 的 坐标为(10,4),∴M(5,2),AB=10,BC=4.OC.∵四边形ABEF为菱形,∴BE=AB=10.过点E作EG⊥AB于点G.在 Rt△BEG中,设EG=4k(k>0),则. ∴k=2.∴EG=8,BG=6.∴AG= 4.∴E(4,12).∵点B的坐标为(10,4),AB∥x轴,∴A(0,4).易知点N为AE 的中点,∴N(2,8).由M,N两点坐标可得直线的表达式为y= -2x+12.故选 D.
二、9.<
点规律 当0°<α<45°时, sinαcosα.
10.45°【点拨】根据题意得Δ=(-2) -4tanα=0,则tanα=1,所以锐角α=45°.
11. 【点拨】∵∠ACB=90°,点D为AB边的中点,∴DC=BD=AD,∴∠DCB =∠B,AB=2CD=6.
故答案为 .
【点拨】在△ABC中,∠C = 90°,∴c =a +b .∵b =ac,∴c =a +ac.等式两边同时除以ac,得 令 则有 ∴x +x-1 =0.解得 (舍去).
【点拨】如图,过点C作 CT⊥y轴于点 T,过点D作 DH⊥CT交 CT的延长线于点 H.
∵tan∠ABO= .设OB=a(a>0),则OA=3a.易证△AOB≌△BTC,∴BT= OA=3a,OB= TC=a.∴OT= BT-OB=2a.∴C(a,2a).∵点C在 的图象上,∴ 易证△CHD≌△BTC,∴DH= CT=a,CH = BT=3a.∴HT=2a.∴D(-2a,3a).设图象经过点D的反比例函数的表达式为 则有-2a·3a=k,∴k=-6a =-3.∴图象经过点D的反比例函数的表达式是
三、14.【解】(1)
(2)(-2) -3tan 30°+|tan 60°-2|
15.【解】∵∠C=90°,AB=5,BC=3,
16.【解】过点 C作CH⊥AB于点H.
根据题意,得∠ACH=30°,∠HCB=45°,CH=138 米.
在Rt△ACH中, (米).
在 Rt△BCH中,∵∠HCB=45°,CH=138米,∴BH=CH=138 米.
(米).
答:“吉塔”的高度约为 218 米.
17.【解】拓展探究
如图,作 CD⊥AB于点 D,AE⊥BC 于点 E.
在 Rt△ABE中,
同理,
∴AE=csin B=bsin∠BCA,CD=asin B=bsin∠BAC.
解决问题
在△ABC中,∠CBA=180°-∠A-∠C=45°.
即点A到点 B的距离为:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
专题 锐角三角函数的计算
一、选择题(每题4分,共32分)
1.下列计算结果正确的是( )
A.(a ) =a
2.在△ABC中,∠C=90°,BC=6,AC=8,则 sin A 的值为( )
3.在正方形网格中,△ABC 的位置如图所示,点A,B,C均在格点上,则 sin∠BAC的值为( )
4.在△ABC 中,∠C =90°,则AC 等于( )
A.3 B.2 C. D.
5.如图,已知点 P(4,3),OP与x轴正半轴的夹角为α,则 cosα=( )
6.如图,以O为圆心,任意长为半径画弧,与射线OA 交于点 B,再以B为圆心,BO 长为半径画弧,两弧交于点 C,画射线OC,则 tan∠AOC的值为( )
D.
7.在△ABC中,∠A、∠B均为锐角,且 则△ABC是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
8.如图,在平面直角坐标系xOy中,矩形 OABC 的顶点 B的坐标为(10,4),四边形ABEF是菱形,且 若直线把矩形OABC 和菱形ABEF组成的图形的面积分成相等的两部分,则直线的表达式为( )
A. y=3x C. y=-2x+11 D. y= -2x+12
二、填空题(每题4分,共20分)
9.比较大小:当0°<α<45°时,sinα___________cosα.(填“>”“<”或“=”)
10.关于x的一元二次方程x -2x+tan α=0有两个相等的实数根,则锐角α=_________.
11.如图,在△ABC中,∠ACB= 90°,点 D为AB边的中点,连接CD,若BC =4,CD=3,则 cos∠DCB 的值为__________.
12.在△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C的对边,若b =ac,则sin A 的值为______________.
13.如图,已知在平面直角坐标系xOy中,点A在x轴的负半轴上,点B在y轴的负半轴上,tan∠ABO=3,以AB为边向上作正方形 ABCD.若图象经过点C的反比例函数的表达式是 则图象经过点 D的反比例函数的表达式是_____________.
三、解答题(共48分)
14.(12分)计算:
(2)(-2) -3tan 30°+|tan 60°-2|.
15.(10分)如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,求AC的长和 sin A 的值.
16.(12分)吉林省广播电视塔(简称“吉塔”)是吉林省省会长春市的标志性建筑之一.某科技兴趣小组利用无人机搭载测量仪器测量“吉塔”的高度,如图,将无人机置于距离“吉塔”138米的点 C 处.从无人机上观测塔尖A的仰角为30°,观测塔基座中心点 B 的俯角为45°.求“吉塔”的高度(结果保留整数,参考数据:
17.(14分)知识再现
如图①,在 Rt△ABC中,∠C= 90°,∠A,∠B,∠C的对边分别为a,b,c.
拓展探究
如图②,在锐角三角形 ABC中,∠A,∠B,∠C的对边分别为a,b,c.
请探究 之间的关系,并写出探究过程.
解决问题
如图③,为测量点A到河对岸点 B的距离,选取与点A 在河岸同一侧的点 C,测得AC=
60m,∠A=75°,∠C=60°.请用拓展探究中的结论,求点 A到点 B的距离.
参考答案
一、1. C 【点拨】 故选 C.
2. C 【点拨】由勾股定理得AB=10,再根据三角函数定义得 故本题选 C.
3. A 【点拨】设小正方形的边长为1,作CD⊥AB交AB 的延长线于点 D.∵在 Rt△ACD中,∠ADC= 故选A.
4. B 【点拨】 故选 B.
5. B 【点拨】过P作PN⊥x轴于N.∵P(4,3),∴ON=4,PN=3,∴在 Rt△PON中,由勾股定理得 OP = 故选B.
6. D 【点拨】如图,连接BC,则由题意可得OC=OB,CB=OB,∴OC= OB=BC,∴△BOC是等边三角形,∴∠AOC= 故选D.
7. B【点拨】∵ 在△ABC中,∠C=180°-60°-60°=60°,∴△ABC是等边三角形.故选 B.
8. D 【点拨】连接OB,AC,交于点M;连接AE,BF,交于点N,过M、N两点作直线,则直线MN为符合条件的直线l,如图所示.∵四边形 OABC 是矩形,∴OM = BM.∵点 B 的 坐标为(10,4),∴M(5,2),AB=10,BC=4.OC.∵四边形ABEF为菱形,∴BE=AB=10.过点E作EG⊥AB于点G.在 Rt△BEG中,设EG=4k(k>0),则. ∴k=2.∴EG=8,BG=6.∴AG= 4.∴E(4,12).∵点B的坐标为(10,4),AB∥x轴,∴A(0,4).易知点N为AE 的中点,∴N(2,8).由M,N两点坐标可得直线的表达式为y= -2x+12.故选 D.
二、9.<
点规律 当0°<α<45°时, sinα
10.45°【点拨】根据题意得Δ=(-2) -4tanα=0,则tanα=1,所以锐角α=45°.
11. 【点拨】∵∠ACB=90°,点D为AB边的中点,∴DC=BD=AD,∴∠DCB =∠B,AB=2CD=6.
故答案为 .
【点拨】在△ABC中,∠C = 90°,∴c =a +b .∵b =ac,∴c =a +ac.等式两边同时除以ac,得 令 则有 ∴x +x-1 =0.解得 (舍去).
【点拨】如图,过点C作 CT⊥y轴于点 T,过点D作 DH⊥CT交 CT的延长线于点 H.
∵tan∠ABO= .设OB=a(a>0),则OA=3a.易证△AOB≌△BTC,∴BT= OA=3a,OB= TC=a.∴OT= BT-OB=2a.∴C(a,2a).∵点C在 的图象上,∴ 易证△CHD≌△BTC,∴DH= CT=a,CH = BT=3a.∴HT=2a.∴D(-2a,3a).设图象经过点D的反比例函数的表达式为 则有-2a·3a=k,∴k=-6a =-3.∴图象经过点D的反比例函数的表达式是
三、14.【解】(1)
(2)(-2) -3tan 30°+|tan 60°-2|
15.【解】∵∠C=90°,AB=5,BC=3,
16.【解】过点 C作CH⊥AB于点H.
根据题意,得∠ACH=30°,∠HCB=45°,CH=138 米.
在Rt△ACH中, (米).
在 Rt△BCH中,∵∠HCB=45°,CH=138米,∴BH=CH=138 米.
(米).
答:“吉塔”的高度约为 218 米.
17.【解】拓展探究
如图,作 CD⊥AB于点 D,AE⊥BC 于点 E.
在 Rt△ABE中,
同理,
∴AE=csin B=bsin∠BCA,CD=asin B=bsin∠BAC.
解决问题
在△ABC中,∠CBA=180°-∠A-∠C=45°.
即点A到点 B的距离为:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
