第二章 直角三角形的边角关系专题 构造三角函数基本图形解实际问题的四种数学模型同步练习(含解析)
文档属性
| 名称 | 第二章 直角三角形的边角关系专题 构造三角函数基本图形解实际问题的四种数学模型同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 21:34:11 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
专题 构造三角函数基本图形解实际问题的四种数学模型
模型1 构造形如 的两个直角三角形解实际问题
1.如图是某种型号跑步机的示意图.已知跑步机手柄 AB与地面 DE 平行,踏板 CD长为
1.5m ,CD与地面 DE 的夹角∠CDE=15°,支架AC 长为1m ,∠ACD=75°,求跑步机手柄AB所在直线与地面 DE 之间的距离(结果精确到0.1m).
模型2 构造形如 的两个直角三角形解实际问题
2.如图,一艘轮船从点 A 处以30 km/h 的速度向正东方向航行,在A 处测得灯塔C 在北偏东60°方向上,继续航行1 h到达B处,这时测得灯塔C 在北偏东45°方向上,已知在灯塔 C的四周4 0 km 内有暗礁,问这艘轮船继续向正东方向航行是否安全 并说明理由(提示:
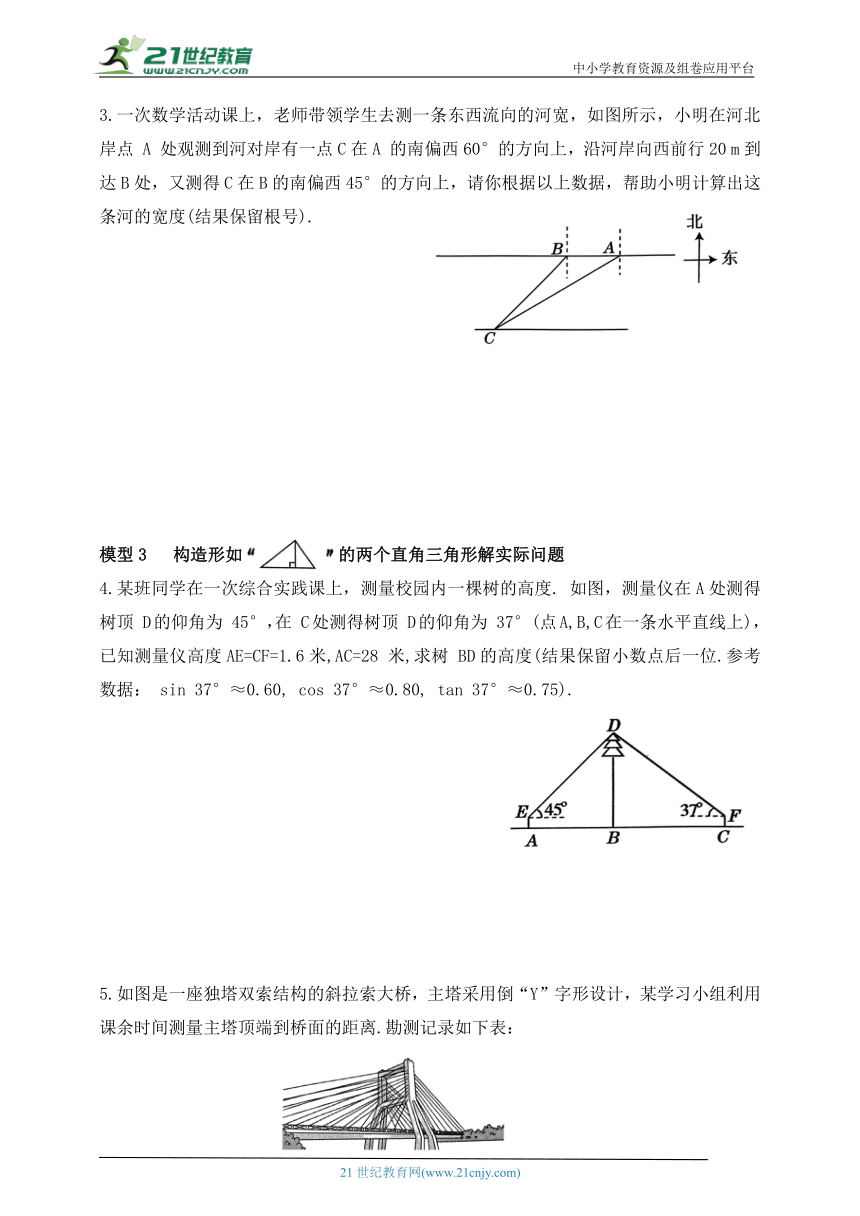
3.一次数学活动课上,老师带领学生去测一条东西流向的河宽,如图所示,小明在河北岸点 A 处观测到河对岸有一点C在A 的南偏西60°的方向上,沿河岸向西前行20 m到达B处,又测得C在B的南偏西45°的方向上,请你根据以上数据,帮助小明计算出这条河的宽度(结果保留根号).
模型3 构造形如 的两个直角三角形解实际问题
4.某班同学在一次综合实践课上,测量校园内一棵树的高度. 如图,测量仪在A处测得树顶 D的仰角为 45°,在 C处测得树顶 D的仰角为 37°(点A,B,C在一条水平直线上),已知测量仪高度AE=CF=1.6米,AC=28 米,求树 BD的高度(结果保留小数点后一位.参考数据: sin 37°≈0.60, cos 37°≈0.80, tan 37°≈0.75).
5.如图是一座独塔双索结构的斜拉索大桥,主塔采用倒“Y”字形设计,某学习小组利用课余时间测量主塔顶端到桥面的距离.勘测记录如下表:
活动内容 测量主塔顶端到桥面的距离
成员 组长:×××组员:×××××××
测量工具 测角仪、皮尺等
测量示意图 说明:左图为斜拉索桥的侧面示意图,点A,C,D,B在同一条直线上,EF⊥AB,点A,C分别与点B,D关于直线EF对称
测量数据 ∠A的大小 28°
AC的长度 84 m
CD的长度 12 m
请利用表中提供的信息,求主塔顶端E到 AB的距离(参考数据:sin 28°≈0.47,cos 28°≈0.88, tan 28°≈0.53).
模型4 构造形如 的两个直角三角形解实际问题
6.一架无人机沿水平直线飞行进行测绘工作,在点 P处测得正前方水平地面上某建筑物AB 的顶端A 的俯角为30°,面向AB方向继续飞行5米,测得该建筑物底端B 的俯角为45°,已知建筑物 AB的高为3米,求无人机飞行的高度(结果精确到1米,参考数据:
参考答案
1.【解】如图,过点 C 作 FG⊥AB于点F,交 DE于点G,则 FG⊥DE.
∵∠CDE=15°,∠ACD=75°,∴∠ACF=∠FCD-∠ACD =∠CGD+∠CDE-∠ACD=90°+15°-75°=30°.∴∠CAF=60°.
在Rt△ACF中,
在Rt△CDG中,CG=CD·sin∠CDE=1.5·sin 15°m,
0.26≈1.3(m).
答:跑步机手柄AB所在直线与地面 DE之间的距离约为1.3m .
2.【解】安全.理由如下:如图,过点 C作CD⊥AB 于点 D.
由题意可得∠CAD=90°-60°=30°,∠CBD=90°-45°=45°,AB=30×1 =30(km).
在 Rt△CBD中,∵∠CDB=90°,∠CBD=45°,∴∠CBD=∠BCD.∴BD=CD.
设CD=BD=x km,则AD=(x+30) km.
在Rt△ACD中, 即 解得
∴CD≈40.98 km.
∵40.98>40,∴这艘轮船继续向正东方向航行是安全的.
点易错 本题图形也称为“母抱子”, 即两个直角三角形有一条公共的直角边,且它们位于该边同侧.
3.【解】如图,过点 C作CD⊥AB于D.
设CD=xm,在 Rt△BCD中,∵∠CBD=90°-45°=45°,∴BD=CD=xm.
在 Rt△ACD中,∠DAC=90°-60°=30°,AD=AB+BD=(20+x)m,CD=xm,
∴CD=tan 30°·AD,即 解得
答:这条河的宽度为
4.【解】如图,连接 EF,交BD于点M,则EF⊥BD,AE=BM=CF=1.6米,
在 Rt△DEM中,∵∠DEM=45°,∴EM=DM.
设DM=x米,则 EM=AB=x米,FM=BC=AC-AB=(28-x)米,
在 Rt△DFM中, 即 解得x≈12,
经检验,x≈12是原方程的根,即DM≈12米,∴DB≈12+1.6=13.6(米).
答:树BD的高度约为 13.6米.
5.【解】如图,延长EF交AB于M,
∵EF⊥AB,点A,C分别与点 B,D关于直线EF对称,CD=12m,
∵∠A=28°,AC=84m, 即
答:主塔顶端E到AB 的距离约为 47.7 m.
6.【解】如图,延长 PQ,BA,相交于点E,
由题意可得 AB⊥PQ,∠E=90°,又∵∠BQE=45°,∴BE=QE.
设BE = QE = x 米,∵PQ=5米,AB=3米,∴PE=(x+5)米,AE=(x-3)米,
∵∠E=90°,
∵∠APE=30°,解得
答:无人机飞行的高度约为 14 米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
专题 构造三角函数基本图形解实际问题的四种数学模型
模型1 构造形如 的两个直角三角形解实际问题
1.如图是某种型号跑步机的示意图.已知跑步机手柄 AB与地面 DE 平行,踏板 CD长为
1.5m ,CD与地面 DE 的夹角∠CDE=15°,支架AC 长为1m ,∠ACD=75°,求跑步机手柄AB所在直线与地面 DE 之间的距离(结果精确到0.1m).
模型2 构造形如 的两个直角三角形解实际问题
2.如图,一艘轮船从点 A 处以30 km/h 的速度向正东方向航行,在A 处测得灯塔C 在北偏东60°方向上,继续航行1 h到达B处,这时测得灯塔C 在北偏东45°方向上,已知在灯塔 C的四周4 0 km 内有暗礁,问这艘轮船继续向正东方向航行是否安全 并说明理由(提示:
3.一次数学活动课上,老师带领学生去测一条东西流向的河宽,如图所示,小明在河北岸点 A 处观测到河对岸有一点C在A 的南偏西60°的方向上,沿河岸向西前行20 m到达B处,又测得C在B的南偏西45°的方向上,请你根据以上数据,帮助小明计算出这条河的宽度(结果保留根号).
模型3 构造形如 的两个直角三角形解实际问题
4.某班同学在一次综合实践课上,测量校园内一棵树的高度. 如图,测量仪在A处测得树顶 D的仰角为 45°,在 C处测得树顶 D的仰角为 37°(点A,B,C在一条水平直线上),已知测量仪高度AE=CF=1.6米,AC=28 米,求树 BD的高度(结果保留小数点后一位.参考数据: sin 37°≈0.60, cos 37°≈0.80, tan 37°≈0.75).
5.如图是一座独塔双索结构的斜拉索大桥,主塔采用倒“Y”字形设计,某学习小组利用课余时间测量主塔顶端到桥面的距离.勘测记录如下表:
活动内容 测量主塔顶端到桥面的距离
成员 组长:×××组员:×××××××
测量工具 测角仪、皮尺等
测量示意图 说明:左图为斜拉索桥的侧面示意图,点A,C,D,B在同一条直线上,EF⊥AB,点A,C分别与点B,D关于直线EF对称
测量数据 ∠A的大小 28°
AC的长度 84 m
CD的长度 12 m
请利用表中提供的信息,求主塔顶端E到 AB的距离(参考数据:sin 28°≈0.47,cos 28°≈0.88, tan 28°≈0.53).
模型4 构造形如 的两个直角三角形解实际问题
6.一架无人机沿水平直线飞行进行测绘工作,在点 P处测得正前方水平地面上某建筑物AB 的顶端A 的俯角为30°,面向AB方向继续飞行5米,测得该建筑物底端B 的俯角为45°,已知建筑物 AB的高为3米,求无人机飞行的高度(结果精确到1米,参考数据:
参考答案
1.【解】如图,过点 C 作 FG⊥AB于点F,交 DE于点G,则 FG⊥DE.
∵∠CDE=15°,∠ACD=75°,∴∠ACF=∠FCD-∠ACD =∠CGD+∠CDE-∠ACD=90°+15°-75°=30°.∴∠CAF=60°.
在Rt△ACF中,
在Rt△CDG中,CG=CD·sin∠CDE=1.5·sin 15°m,
0.26≈1.3(m).
答:跑步机手柄AB所在直线与地面 DE之间的距离约为1.3m .
2.【解】安全.理由如下:如图,过点 C作CD⊥AB 于点 D.
由题意可得∠CAD=90°-60°=30°,∠CBD=90°-45°=45°,AB=30×1 =30(km).
在 Rt△CBD中,∵∠CDB=90°,∠CBD=45°,∴∠CBD=∠BCD.∴BD=CD.
设CD=BD=x km,则AD=(x+30) km.
在Rt△ACD中, 即 解得
∴CD≈40.98 km.
∵40.98>40,∴这艘轮船继续向正东方向航行是安全的.
点易错 本题图形也称为“母抱子”, 即两个直角三角形有一条公共的直角边,且它们位于该边同侧.
3.【解】如图,过点 C作CD⊥AB于D.
设CD=xm,在 Rt△BCD中,∵∠CBD=90°-45°=45°,∴BD=CD=xm.
在 Rt△ACD中,∠DAC=90°-60°=30°,AD=AB+BD=(20+x)m,CD=xm,
∴CD=tan 30°·AD,即 解得
答:这条河的宽度为
4.【解】如图,连接 EF,交BD于点M,则EF⊥BD,AE=BM=CF=1.6米,
在 Rt△DEM中,∵∠DEM=45°,∴EM=DM.
设DM=x米,则 EM=AB=x米,FM=BC=AC-AB=(28-x)米,
在 Rt△DFM中, 即 解得x≈12,
经检验,x≈12是原方程的根,即DM≈12米,∴DB≈12+1.6=13.6(米).
答:树BD的高度约为 13.6米.
5.【解】如图,延长EF交AB于M,
∵EF⊥AB,点A,C分别与点 B,D关于直线EF对称,CD=12m,
∵∠A=28°,AC=84m, 即
答:主塔顶端E到AB 的距离约为 47.7 m.
6.【解】如图,延长 PQ,BA,相交于点E,
由题意可得 AB⊥PQ,∠E=90°,又∵∠BQE=45°,∴BE=QE.
设BE = QE = x 米,∵PQ=5米,AB=3米,∴PE=(x+5)米,AE=(x-3)米,
∵∠E=90°,
∵∠APE=30°,解得
答:无人机飞行的高度约为 14 米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
