第二章 直角三角形的边角关系专题 解直角三角形及其应用同步练习(含解析)
文档属性
| 名称 | 第二章 直角三角形的边角关系专题 解直角三角形及其应用同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 21:36:03 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
专题 解直角三角形及其应用
一、选择题(每题4分,共32分)
1.在 Rt△ABC中,∠C=则AB等于( )
A.15 B.12 C.9 D.6
2.如图,圆规两脚OA,OB张开的角度∠AOB为α,OA=OB=10,则两脚张开的距离AB为( )
A.10sinα B.10cosα
3.如图,在四边形 ABCD中, ∥BC=10,则AB的长是( )
A.3 B.6 C.8 D.9
4.如图,小明利用一个锐角是30°的三角尺测操场旗杆的高度,已知他与旗杆之间的水平距离BC为15 m,AB为1.5m (即小明的眼睛与地面的距离),那么旗杆的高度是( )
5.如图是某商场营业大厅自动扶梯的示意图,自动扶梯AB的倾斜角为37°,大厅两层之间的距离 BC 为6m,则自动扶梯AB 的长约为(sin37°≈0.6,cos 37°≈0.8, tan 37°≈0.75)( )
A.7.5 m B.8 m C.9 m D.10 m
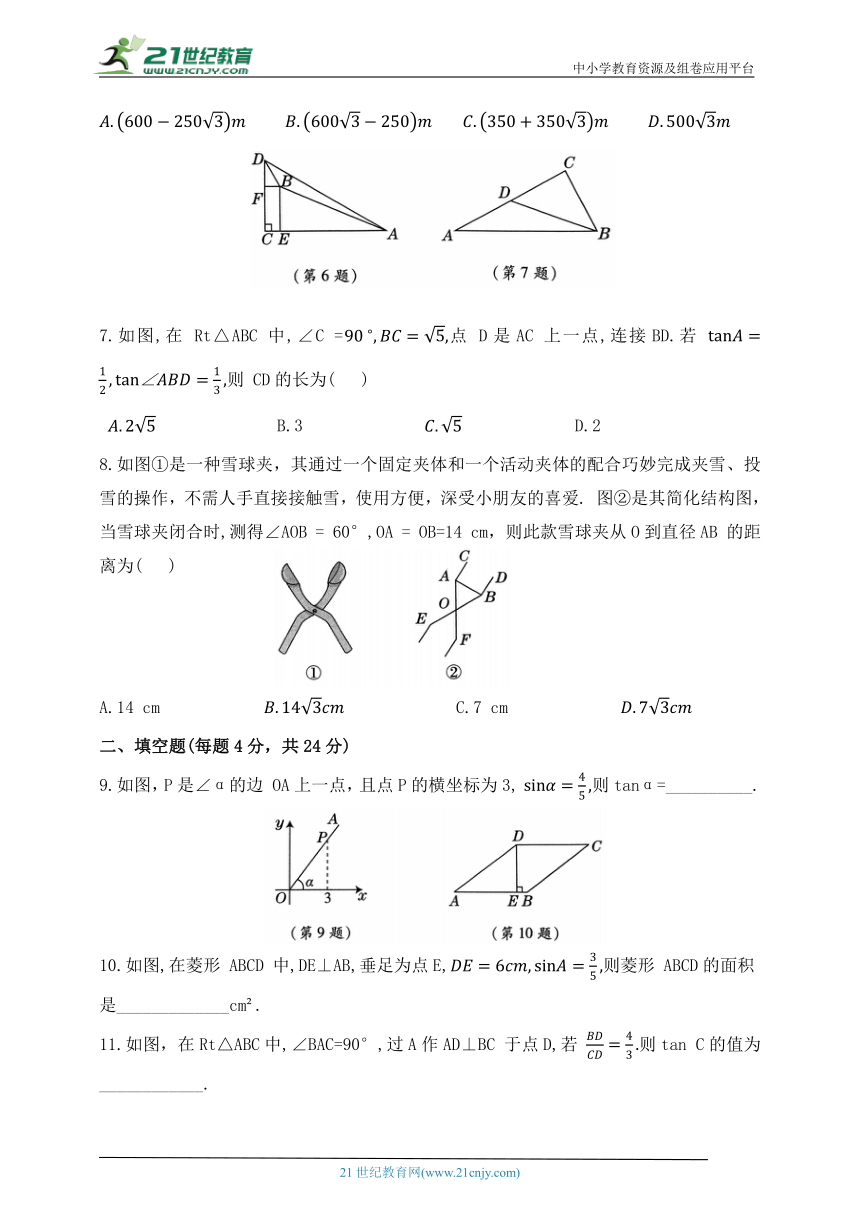
6.如图,小明去爬山,在山脚A 处看山顶 D的角度为30°,小明在坡比为5:12 的山坡 AB上走1 300m,此时小明在B处看山顶D的角度为60°,则山高为( )
7.如图,在 Rt△ABC 中,∠C =点 D是AC 上一点,连接BD.若 则 CD的长为( )
B.3 D.2
8.如图①是一种雪球夹,其通过一个固定夹体和一个活动夹体的配合巧妙完成夹雪、投雪的操作,不需人手直接接触雪,使用方便,深受小朋友的喜爱. 图②是其简化结构图,当雪球夹闭合时,测得∠AOB = 60°,OA = OB=14 cm,则此款雪球夹从O到直径AB 的距离为( )
A.14 cm C.7 cm
二、填空题(每题4分,共24分)
9.如图,P是∠α的边 OA上一点,且点P的横坐标为3, 则tanα=__________.
10.如图,在菱形 ABCD 中,DE⊥AB,垂足为点E,则菱形 ABCD的面积
是_____________cm .
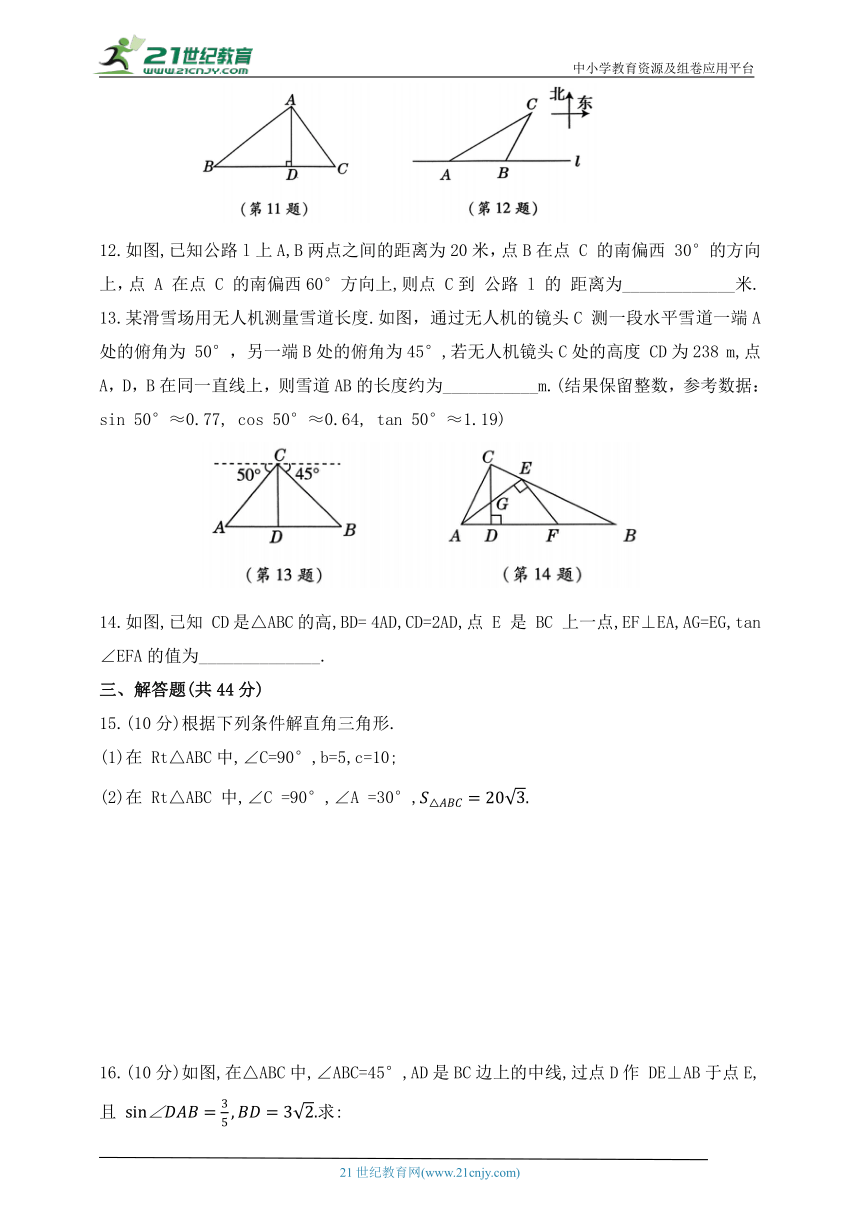
11.如图,在Rt△ABC中,∠BAC=90°,过A作AD⊥BC 于点D,若 则tan C的值为____________.
12.如图,已知公路l上A,B两点之间的距离为20米,点B在点 C 的南偏西 30°的方向上,点 A 在点 C 的南偏西60°方向上,则点 C到 公路 l 的 距离为_____________米.
13.某滑雪场用无人机测量雪道长度.如图,通过无人机的镜头C 测一段水平雪道一端A 处的俯角为 50°,另一端B处的俯角为45°,若无人机镜头C处的高度 CD为238 m,点A,D,B在同一直线上,则雪道AB的长度约为___________m.(结果保留整数,参考数据:
sin 50°≈0.77, cos 50°≈0.64, tan 50°≈1.19)
14.如图,已知 CD是△ABC的高,BD= 4AD,CD=2AD,点 E 是 BC 上一点,EF⊥EA,AG=EG,tan∠EFA的值为______________.
三、解答题(共44分)
15.(10分)根据下列条件解直角三角形.
(1)在 Rt△ABC中,∠C=90°,b=5,c=10;
(2)在 Rt△ABC 中,∠C =90°,∠A =30°,
16.(10分)如图,在△ABC中,∠ABC=45°,AD是BC边上的中线,过点D作 DE⊥AB于点E,
且 求:
(1)AB 的长;
(2)∠CAB的正切值.
17.(12分)如图所示,我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度.小宇同学在A 处观测对岸 C点,测得∠CAD=45°,小英同学在距 A 处50米远的 B处测得∠CBD=30°,请你根据这些数据算出河宽(精确到0.1 米,参考数据 1.732).
18.(12分)3月份,长江重庆段开始进入枯水期,有些航道狭窄的水域通航压力开始慢慢增加.为及时掌握辖区通航环境实时情况,严防船舶搁浅、触礁等险情事故发生,沿江海事执法人员持续开展巡航检查,确保近七百公里的长江干线通航安全. 如图,巡航船在一段自西向东的航道上的A处发现,航标 B在A 处的北偏东45°方向200米处,以航标B为圆心,150米长为半径的圆形区域内有浅滩,会使过往船舶有危险.
(1)由于水位下降,巡航船还发现在A 处北偏西15°方向300米的 C 处,露出一片礁石,求B、C两地的距离(精确到1米);
(2)为保证航道畅通,航道维护项目部会组织挖泥船对该条航道被浅滩影响的航段进行保
航施工.请判断该条航道是否被这片浅滩区域影响 如果有被影响,请求出被影响的航道长度为多少米 如果没有被影响,请说明理由.
(参考数据:
参考答案
一、1. A 【点拨】因为在 Rt△ABC 中,∠C=90°,AC=9,所以 所以AB=15.故选 A.
2. C【点拨】过点O作OC⊥AB,垂足为C,∵OA=O在 Rt△COB中,( 故选 C.
3. B 【点拨】因为AD=DC,所以∠DAC=∠DCA.又因为AD∥BC,所以∠DAC=∠ACB,所以∠DCA=∠ACB.在 Rt△ACB中, 则
4. D 【点拨】由题意可得,四边形 ABCD是矩形,∴BC=AD=15 m,AB= CD=1.5m ,在 Rt△ADE中,∠EAD=30°,AD = 15 m,∴DE =AD·tan∠EAD=故选 D.
5. D 【点拨】根据题意,得 故选 D.
6. B 【点拨】∵BE:AE =5:12,∴可设BE =5k,AE=12k.∵AB =1 300 m,∴在 Rt△ABE中,由勾股定理,得AE +BE = AB ,即(12k) +(5k) =1300 ,解得k=100.∴AE =1 200 m,CF=BE =500 m.设 又 解得: 即山高为 故选B.
7. C 【点拨】在 Rt△ABC中,∵ 由勾股定理得,过点 D作DE⊥AB 于点 E, ∴DE= 1.在 Rt△ADE 中,∵AD = AE + DE ,
故选C.
8. D 【点拨】作OG⊥AB于点 G.∵OA=OB=14 cm,∠AOB=60°,∴∠AOG=∠BOG=30°.∴OG=OA·故选 D.
二、9. 【点拨】由 点P的横坐标为3,易得点P的纵坐标为 4,∴tanα就等于点P的纵坐标与其横坐标的比值,∴
10.60【点拨】在 Rt△ADE中, ∵DE=6cm,∴AD= 10 cm.∵四边形ABCD为菱形,∴ 6=60(cm ).
【点拨】 设BD=4x,CD=3x.
∵AD⊥BC,∴∠ADB =∠ADC =∠BAC = 90°,∴∠BAD+∠CAD=∠C+∠DAC,∴∠C=∠BAD,
【点拨】如图,过点 CC.作CD⊥公路于点D,则东∠ADC=90°.
∵∠BCD=30°,∠ACD=60°,∴∠ACB =∠ACD-∠BCD= 60°-30°=30°,∠CAD=90°-∠ACD =90°-60°=30°,∴∠ACB=∠CAD,∴BC=AB=20米.在Rt△BCD中, (米).
13.438 【点拨】由题意得,∠CAD=50°,∠CBD=45°,在 Rt△CBD中,∠CBD=45°,∴BD=CD=
238 m. 在 Rt△CAD中,
【点拨】设AD=x,则 CD=2x,BD=4x.∵CD是△ABC 的高,∴∠CDA=∠BDC=90°.
又∵ ∵∠CAD+∠ACD=90°,∴∠ACD+∠BCD=90°,即∠ACB=90°.在Rt△ACE中,∵AG=GE,∴CG= 90°.∵∠DAE +∠AGD = 90°,∴∠AGD=∠EFA.设DG=t,则AG=CG=2x-t,则.x +t =(2x-t) ,解得
三、15.【解】(1)在 Rt△ABC中,∠C=90°,b=5,c=
(2)∵∠A=30°,∠C=90°,
16.【解】(1)∵ ∴BE=DE=3.
(2)如图,过点 C作 CH⊥AB于点 H.
∵AD是BC边上的中线,
∵∠ABC=45°,∴BH=CH=6.∴AH=1.
17.【解】如图,过C作 CE⊥AB于E,设CE=x米,在Rt△AEC中,∠CAE=45°,∴AE=CE=x米.在Rt△BCE中, 米.
∵AB=50米, 解得
答:河宽约为 68.3米.
18.【解】(1)如图,过点B作 BD⊥AC 于点 D,
由题意得,∠BAC = 15°+45°=60°,AB=200 米,AC=300米,
在Rt△ABD中, 解得米,AD=100米,∴CD=AC-AD=200 米,
由勾股定理得, 265(米).
∴B、C两地的距离约为265米.
(2)该条航道会被这片浅滩区域影响,长度为 100米.理由如下:如图,过点B作航道的垂线 BE,由题意得,AB=200米,∠BAE=45°,在Rt△ABE中, 解得BE=100 米≈141米.
∵141<150,∴该条航道会被这片浅滩区域影响.在AE上取一点F,连接BF,使BF= 150米,在Rt△BEF中, (米),根据对称性可知,被影响的航道长度为100米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
专题 解直角三角形及其应用
一、选择题(每题4分,共32分)
1.在 Rt△ABC中,∠C=则AB等于( )
A.15 B.12 C.9 D.6
2.如图,圆规两脚OA,OB张开的角度∠AOB为α,OA=OB=10,则两脚张开的距离AB为( )
A.10sinα B.10cosα
3.如图,在四边形 ABCD中, ∥BC=10,则AB的长是( )
A.3 B.6 C.8 D.9
4.如图,小明利用一个锐角是30°的三角尺测操场旗杆的高度,已知他与旗杆之间的水平距离BC为15 m,AB为1.5m (即小明的眼睛与地面的距离),那么旗杆的高度是( )
5.如图是某商场营业大厅自动扶梯的示意图,自动扶梯AB的倾斜角为37°,大厅两层之间的距离 BC 为6m,则自动扶梯AB 的长约为(sin37°≈0.6,cos 37°≈0.8, tan 37°≈0.75)( )
A.7.5 m B.8 m C.9 m D.10 m
6.如图,小明去爬山,在山脚A 处看山顶 D的角度为30°,小明在坡比为5:12 的山坡 AB上走1 300m,此时小明在B处看山顶D的角度为60°,则山高为( )
7.如图,在 Rt△ABC 中,∠C =点 D是AC 上一点,连接BD.若 则 CD的长为( )
B.3 D.2
8.如图①是一种雪球夹,其通过一个固定夹体和一个活动夹体的配合巧妙完成夹雪、投雪的操作,不需人手直接接触雪,使用方便,深受小朋友的喜爱. 图②是其简化结构图,当雪球夹闭合时,测得∠AOB = 60°,OA = OB=14 cm,则此款雪球夹从O到直径AB 的距离为( )
A.14 cm C.7 cm
二、填空题(每题4分,共24分)
9.如图,P是∠α的边 OA上一点,且点P的横坐标为3, 则tanα=__________.
10.如图,在菱形 ABCD 中,DE⊥AB,垂足为点E,则菱形 ABCD的面积
是_____________cm .
11.如图,在Rt△ABC中,∠BAC=90°,过A作AD⊥BC 于点D,若 则tan C的值为____________.
12.如图,已知公路l上A,B两点之间的距离为20米,点B在点 C 的南偏西 30°的方向上,点 A 在点 C 的南偏西60°方向上,则点 C到 公路 l 的 距离为_____________米.
13.某滑雪场用无人机测量雪道长度.如图,通过无人机的镜头C 测一段水平雪道一端A 处的俯角为 50°,另一端B处的俯角为45°,若无人机镜头C处的高度 CD为238 m,点A,D,B在同一直线上,则雪道AB的长度约为___________m.(结果保留整数,参考数据:
sin 50°≈0.77, cos 50°≈0.64, tan 50°≈1.19)
14.如图,已知 CD是△ABC的高,BD= 4AD,CD=2AD,点 E 是 BC 上一点,EF⊥EA,AG=EG,tan∠EFA的值为______________.
三、解答题(共44分)
15.(10分)根据下列条件解直角三角形.
(1)在 Rt△ABC中,∠C=90°,b=5,c=10;
(2)在 Rt△ABC 中,∠C =90°,∠A =30°,
16.(10分)如图,在△ABC中,∠ABC=45°,AD是BC边上的中线,过点D作 DE⊥AB于点E,
且 求:
(1)AB 的长;
(2)∠CAB的正切值.
17.(12分)如图所示,我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度.小宇同学在A 处观测对岸 C点,测得∠CAD=45°,小英同学在距 A 处50米远的 B处测得∠CBD=30°,请你根据这些数据算出河宽(精确到0.1 米,参考数据 1.732).
18.(12分)3月份,长江重庆段开始进入枯水期,有些航道狭窄的水域通航压力开始慢慢增加.为及时掌握辖区通航环境实时情况,严防船舶搁浅、触礁等险情事故发生,沿江海事执法人员持续开展巡航检查,确保近七百公里的长江干线通航安全. 如图,巡航船在一段自西向东的航道上的A处发现,航标 B在A 处的北偏东45°方向200米处,以航标B为圆心,150米长为半径的圆形区域内有浅滩,会使过往船舶有危险.
(1)由于水位下降,巡航船还发现在A 处北偏西15°方向300米的 C 处,露出一片礁石,求B、C两地的距离(精确到1米);
(2)为保证航道畅通,航道维护项目部会组织挖泥船对该条航道被浅滩影响的航段进行保
航施工.请判断该条航道是否被这片浅滩区域影响 如果有被影响,请求出被影响的航道长度为多少米 如果没有被影响,请说明理由.
(参考数据:
参考答案
一、1. A 【点拨】因为在 Rt△ABC 中,∠C=90°,AC=9,所以 所以AB=15.故选 A.
2. C【点拨】过点O作OC⊥AB,垂足为C,∵OA=O在 Rt△COB中,( 故选 C.
3. B 【点拨】因为AD=DC,所以∠DAC=∠DCA.又因为AD∥BC,所以∠DAC=∠ACB,所以∠DCA=∠ACB.在 Rt△ACB中, 则
4. D 【点拨】由题意可得,四边形 ABCD是矩形,∴BC=AD=15 m,AB= CD=1.5m ,在 Rt△ADE中,∠EAD=30°,AD = 15 m,∴DE =AD·tan∠EAD=故选 D.
5. D 【点拨】根据题意,得 故选 D.
6. B 【点拨】∵BE:AE =5:12,∴可设BE =5k,AE=12k.∵AB =1 300 m,∴在 Rt△ABE中,由勾股定理,得AE +BE = AB ,即(12k) +(5k) =1300 ,解得k=100.∴AE =1 200 m,CF=BE =500 m.设 又 解得: 即山高为 故选B.
7. C 【点拨】在 Rt△ABC中,∵ 由勾股定理得,过点 D作DE⊥AB 于点 E, ∴DE= 1.在 Rt△ADE 中,∵AD = AE + DE ,
故选C.
8. D 【点拨】作OG⊥AB于点 G.∵OA=OB=14 cm,∠AOB=60°,∴∠AOG=∠BOG=30°.∴OG=OA·故选 D.
二、9. 【点拨】由 点P的横坐标为3,易得点P的纵坐标为 4,∴tanα就等于点P的纵坐标与其横坐标的比值,∴
10.60【点拨】在 Rt△ADE中, ∵DE=6cm,∴AD= 10 cm.∵四边形ABCD为菱形,∴ 6=60(cm ).
【点拨】 设BD=4x,CD=3x.
∵AD⊥BC,∴∠ADB =∠ADC =∠BAC = 90°,∴∠BAD+∠CAD=∠C+∠DAC,∴∠C=∠BAD,
【点拨】如图,过点 CC.作CD⊥公路于点D,则东∠ADC=90°.
∵∠BCD=30°,∠ACD=60°,∴∠ACB =∠ACD-∠BCD= 60°-30°=30°,∠CAD=90°-∠ACD =90°-60°=30°,∴∠ACB=∠CAD,∴BC=AB=20米.在Rt△BCD中, (米).
13.438 【点拨】由题意得,∠CAD=50°,∠CBD=45°,在 Rt△CBD中,∠CBD=45°,∴BD=CD=
238 m. 在 Rt△CAD中,
【点拨】设AD=x,则 CD=2x,BD=4x.∵CD是△ABC 的高,∴∠CDA=∠BDC=90°.
又∵ ∵∠CAD+∠ACD=90°,∴∠ACD+∠BCD=90°,即∠ACB=90°.在Rt△ACE中,∵AG=GE,∴CG= 90°.∵∠DAE +∠AGD = 90°,∴∠AGD=∠EFA.设DG=t,则AG=CG=2x-t,则.x +t =(2x-t) ,解得
三、15.【解】(1)在 Rt△ABC中,∠C=90°,b=5,c=
(2)∵∠A=30°,∠C=90°,
16.【解】(1)∵ ∴BE=DE=3.
(2)如图,过点 C作 CH⊥AB于点 H.
∵AD是BC边上的中线,
∵∠ABC=45°,∴BH=CH=6.∴AH=1.
17.【解】如图,过C作 CE⊥AB于E,设CE=x米,在Rt△AEC中,∠CAE=45°,∴AE=CE=x米.在Rt△BCE中, 米.
∵AB=50米, 解得
答:河宽约为 68.3米.
18.【解】(1)如图,过点B作 BD⊥AC 于点 D,
由题意得,∠BAC = 15°+45°=60°,AB=200 米,AC=300米,
在Rt△ABD中, 解得米,AD=100米,∴CD=AC-AD=200 米,
由勾股定理得, 265(米).
∴B、C两地的距离约为265米.
(2)该条航道会被这片浅滩区域影响,长度为 100米.理由如下:如图,过点B作航道的垂线 BE,由题意得,AB=200米,∠BAE=45°,在Rt△ABE中, 解得BE=100 米≈141米.
∵141<150,∴该条航道会被这片浅滩区域影响.在AE上取一点F,连接BF,使BF= 150米,在Rt△BEF中, (米),根据对称性可知,被影响的航道长度为100米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
