第二章 直角三角形的边角关系章末复习题(含解析)
文档属性
| 名称 | 第二章 直角三角形的边角关系章末复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-29 21:41:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
章末复习
考点1 两个概念
概念1 锐角三角函数
1.在 Rt△ABC 中,∠C =90°,,则cos A=____________.
2.如图,根据提供的数据回答下列问题:
(1)在图①中, sin A =____________, cos A =__________,sin A+cos A=___________;
在图②中,sinA =______________,c osA =___________,sin A +cos A =_____________.
通过以上两个特殊例子,你发现了什么规律 用一个一般式表示出你的发现并加以证明.
(2)利用你发现的规律求解以下题目:
已知β是锐角,且满足 sinβ=3cosβ,求 sinβ,cosβ的值.
概念2 解直角三角形
3.如图,在矩形 ABCD中,点E在 DC上,将矩形沿AE折叠,使点D落在BC边上的点 F处.若AB=3,BC=5,则tan∠DAE的值为( )
4.如图,Rt△ABC 中, 点D是边 BC 的中点,以AD为底边在其右侧作等腰三角形ADE,使∠ADE=∠B,连接CE,则的值为( )
D.2
考点2 一个运算——特殊角的三角函数值与实数的运算
5.在△ABC中,已知∠A、∠B都是锐角 那么∠C 的度数为_______________°.
6.计算:
(1)sin 30°+tan 60°-sin 45°+cos 30°;
考点3 两个应用
应用1 锐角三角函数在学科内的应用
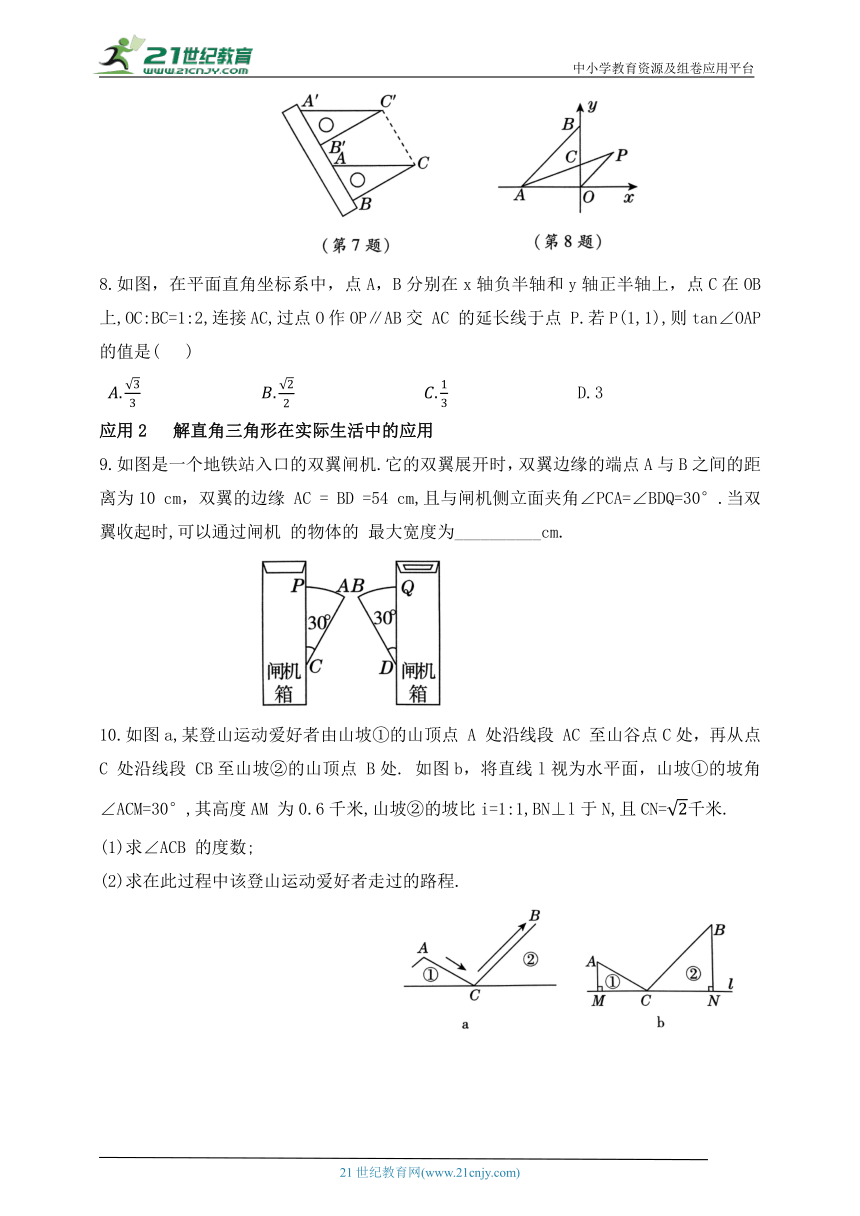
7.如图,现有一把直尺和一块三角尺,其中∠ABC = 90°,∠CAB=60°,AB=8,点A 对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到△A'B'C',点A'对应直尺的刻度为0,则四边形 ACC'A'的面积是( )
A.96 C.192
8.如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上,OC:BC=1:2,连接AC,过点O作OP∥AB交 AC 的延长线于点 P.若P(1,1),则tan∠OAP的值是( )
D.3
应用2 解直角三角形在实际生活中的应用
9.如图是一个地铁站入口的双翼闸机.它的双翼展开时,双翼边缘的端点A与B之间的距离为10 cm,双翼的边缘 AC = BD =54 cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机 的物体的 最大宽度为__________cm.
10.如图a,某登山运动爱好者由山坡①的山顶点 A 处沿线段 AC 至山谷点C处,再从点 C 处沿线段 CB至山坡②的山顶点 B处. 如图b,将直线l视为水平面,山坡①的坡角∠ACM=30°,其高度AM 为0.6千米,山坡②的坡比i=1:1,BN⊥l于N,且CN=千米.
(1)求∠ACB 的度数;
(2)求在此过程中该登山运动爱好者走过的路程.
考点4 两个技巧
技巧1 化斜为直法
11.如图,在△ABC中,AC=2,∠A =15°,∠B=30°,则△ABC的面积为__________.
12.通过学习锐角三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此两条边长的比值与角的大小之间可以相互转化.类似地,可以在等
腰三角形中建立边角之间的联系. 我们定义:等腰三角形中底边与腰的比叫做底角的邻对(记作can).如图①,在△ABC 中,AB =AC,底角 B的邻对记作 can B,这时can B = 容易知道一个角的大小与这个角的邻对值也是一一对应的. 根据上述角的邻对的定义,解答下列问题:
(1) can 30°=____________;
(2)如图②,在△ABC中, 求△ABC的周长.
技巧2 割补法
13.如图①是一个手机支架,图②是其侧面示意图,AB,BC可分别绕点A,B转动,经测量,BC =8cm ,AB=16 cm. 当 AB,BC 转动到 ∠BAE = 60°,∠ABC=50°时,求点 C 到 AE 的距离(结果保留小数点后一位).
参考数据:sin 70°≈0.94,c os70°≈0.34,
cos 50°≈0.64, tan 50°≈1.19.
参考答案
【点拨】由勾股定理,得 所以
2.【解】
规律:对于任意锐角 α,有sin α+cos α= 1.
证明如下:在Rt△A'B'C'中,∠C'=90°,a,b,c分别为∠A',∠B',∠C'的对边,如图所示.
(2)∵β为锐角,∴sinβ>0,cosβ>0.
由 解得 故 sinβ的值为 cosβ的值为
3. D 【点拨】因为四边形ABCD为矩形,所以AD=BC=5,AB=CD=3,因为矩形ABCD沿直线AE折叠,顶点 D恰好落在BC 边上的 F处,所以AF=AD=5,EF=DE,在Rt△ABF中, 所以CF=BC-BF=5-4=1,设CE=x,则 DE=EF=3-x,在 Rt△ECF中,因为CE +FC =EF ,所以x +1 = (3-x) ,解得 所以所以 故选D.
4. D 【点拨】如图,设DE交AC于点T,过点 E作EH⊥CD于点 H.
∵在Rt△ABC中,点D是边BC 的中点,∴AD= DB = DC.∴∠B=∠DAB.
∵∠B=∠ADE,∴∠DAB=∠ADE. ∴ AB∥DE.∴∠DTC=∠BAC=90°.
∵DT∥AB,BD=DC,∴AT=∴ EA = EC = ED. ∴∠EDC= ∠ECD.
∵EH⊥CD,∴ CH = DH.∵DE∥AB,∴∠EDC=
5.105 【点拨】 1,∴∠A = 30°,∠B= 45°,∴∠C = 180°-30°-45°=105°.
6.【解】(1)原式
(2)原式
(3)原式
7. B 【点拨】由题意,得四边形 ACC'A'为平行四边形, .∴AC= 2AB. ∴ 平行四边形 ACC'A'的面积=故选 B.
8. C 【点拨】如图,过点P作PQ⊥x轴于点 Q.
∵OP∥AB,∴∠CAB=∠CPO,∠ABC=∠COP.∴△OCP∽△BCA.∴CP:AC = OC :BC =1:2.
∵∠AOC=∠AQP=90°,∴CO∥PQ.∴OQ:AO=CP:AC=1:2.∵P(1,1),∴PQ=OQ=1.∴AO=
9.64 【点拨】如图,连接AB,CD,过点 A 作AE⊥CD于E,过点B作BF⊥CD于F.
∵AB∥EF,AE∥BF,∴四边形 ABFE 是平行四边形.
∵∠AEF = 90°,∴四边形 AEFB 是矩形,∴EF=AB=10 cm,
∵AE∥PC,∴∠PCA =∠CAE=30°,∴CE= AC·sin30°=27cm,同理可得DF= 27 cm,
∴CD= CE + EF+DF=27+10+27=64(cm).
10.【解】(1)∵山坡②的坡比i=1:1,∴CN=BN.
∴∠BCN=45°.∴∠ACB=180°-30°-45°=105°.
(2)在 Rt△ACM 中,∠AMC =90°,∠ACM=30°,AM=0.6千米,∴AC=2AM=1.2 千米.
在 Rt△BCN中,∠BNC=90°,∠BCN=45°,CN= =千米,∴ 千米.
∴AC+BC=1.2+2=3.2(千米).
答:在此过程中该登山运动爱好者走过的路程为3.2千米.
【点拨】如图,过点D.A作AD⊥BC 交BC 的延长线于点D,
∵AD⊥BC,∴∠ADB=90°.
∵∠CAB=15°,∠B=30°,∴∠DCA=30°+15°=45°,AB=2AD,∴AD=CD.
在Rt△ADC中,·
12.【解】(1)
(2)过点A作AE⊥BC 于点E.
设BC=8x,AB=5x,
解得 (负值舍去),
∴△ABC的周长为
13.【解】如图,过点 B作 BD⊥AE于点 D,延长BC 交 AE于点 N,过点 C作 CM⊥AE于点M.
在Rt△ABD中,∠A=60°,AB=16 cm,
∵∠BAE=60°,∠ABC=50°,∴∠ANB=70°.
在 Rt△NBD中,
∴CN≈14.72-8 =6.72(cm).
在 Rt△CNM中,∠CNM=70°,CN≈6.72 cm,
答:点C到AE 的距离为6.3 cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
章末复习
考点1 两个概念
概念1 锐角三角函数
1.在 Rt△ABC 中,∠C =90°,,则cos A=____________.
2.如图,根据提供的数据回答下列问题:
(1)在图①中, sin A =____________, cos A =__________,sin A+cos A=___________;
在图②中,sinA =______________,c osA =___________,sin A +cos A =_____________.
通过以上两个特殊例子,你发现了什么规律 用一个一般式表示出你的发现并加以证明.
(2)利用你发现的规律求解以下题目:
已知β是锐角,且满足 sinβ=3cosβ,求 sinβ,cosβ的值.
概念2 解直角三角形
3.如图,在矩形 ABCD中,点E在 DC上,将矩形沿AE折叠,使点D落在BC边上的点 F处.若AB=3,BC=5,则tan∠DAE的值为( )
4.如图,Rt△ABC 中, 点D是边 BC 的中点,以AD为底边在其右侧作等腰三角形ADE,使∠ADE=∠B,连接CE,则的值为( )
D.2
考点2 一个运算——特殊角的三角函数值与实数的运算
5.在△ABC中,已知∠A、∠B都是锐角 那么∠C 的度数为_______________°.
6.计算:
(1)sin 30°+tan 60°-sin 45°+cos 30°;
考点3 两个应用
应用1 锐角三角函数在学科内的应用
7.如图,现有一把直尺和一块三角尺,其中∠ABC = 90°,∠CAB=60°,AB=8,点A 对应直尺的刻度为12.将该三角尺沿着直尺边缘平移,使得△ABC移动到△A'B'C',点A'对应直尺的刻度为0,则四边形 ACC'A'的面积是( )
A.96 C.192
8.如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上,OC:BC=1:2,连接AC,过点O作OP∥AB交 AC 的延长线于点 P.若P(1,1),则tan∠OAP的值是( )
D.3
应用2 解直角三角形在实际生活中的应用
9.如图是一个地铁站入口的双翼闸机.它的双翼展开时,双翼边缘的端点A与B之间的距离为10 cm,双翼的边缘 AC = BD =54 cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机 的物体的 最大宽度为__________cm.
10.如图a,某登山运动爱好者由山坡①的山顶点 A 处沿线段 AC 至山谷点C处,再从点 C 处沿线段 CB至山坡②的山顶点 B处. 如图b,将直线l视为水平面,山坡①的坡角∠ACM=30°,其高度AM 为0.6千米,山坡②的坡比i=1:1,BN⊥l于N,且CN=千米.
(1)求∠ACB 的度数;
(2)求在此过程中该登山运动爱好者走过的路程.
考点4 两个技巧
技巧1 化斜为直法
11.如图,在△ABC中,AC=2,∠A =15°,∠B=30°,则△ABC的面积为__________.
12.通过学习锐角三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此两条边长的比值与角的大小之间可以相互转化.类似地,可以在等
腰三角形中建立边角之间的联系. 我们定义:等腰三角形中底边与腰的比叫做底角的邻对(记作can).如图①,在△ABC 中,AB =AC,底角 B的邻对记作 can B,这时can B = 容易知道一个角的大小与这个角的邻对值也是一一对应的. 根据上述角的邻对的定义,解答下列问题:
(1) can 30°=____________;
(2)如图②,在△ABC中, 求△ABC的周长.
技巧2 割补法
13.如图①是一个手机支架,图②是其侧面示意图,AB,BC可分别绕点A,B转动,经测量,BC =8cm ,AB=16 cm. 当 AB,BC 转动到 ∠BAE = 60°,∠ABC=50°时,求点 C 到 AE 的距离(结果保留小数点后一位).
参考数据:sin 70°≈0.94,c os70°≈0.34,
cos 50°≈0.64, tan 50°≈1.19.
参考答案
【点拨】由勾股定理,得 所以
2.【解】
规律:对于任意锐角 α,有sin α+cos α= 1.
证明如下:在Rt△A'B'C'中,∠C'=90°,a,b,c分别为∠A',∠B',∠C'的对边,如图所示.
(2)∵β为锐角,∴sinβ>0,cosβ>0.
由 解得 故 sinβ的值为 cosβ的值为
3. D 【点拨】因为四边形ABCD为矩形,所以AD=BC=5,AB=CD=3,因为矩形ABCD沿直线AE折叠,顶点 D恰好落在BC 边上的 F处,所以AF=AD=5,EF=DE,在Rt△ABF中, 所以CF=BC-BF=5-4=1,设CE=x,则 DE=EF=3-x,在 Rt△ECF中,因为CE +FC =EF ,所以x +1 = (3-x) ,解得 所以所以 故选D.
4. D 【点拨】如图,设DE交AC于点T,过点 E作EH⊥CD于点 H.
∵在Rt△ABC中,点D是边BC 的中点,∴AD= DB = DC.∴∠B=∠DAB.
∵∠B=∠ADE,∴∠DAB=∠ADE. ∴ AB∥DE.∴∠DTC=∠BAC=90°.
∵DT∥AB,BD=DC,∴AT=∴ EA = EC = ED. ∴∠EDC= ∠ECD.
∵EH⊥CD,∴ CH = DH.∵DE∥AB,∴∠EDC=
5.105 【点拨】 1,∴∠A = 30°,∠B= 45°,∴∠C = 180°-30°-45°=105°.
6.【解】(1)原式
(2)原式
(3)原式
7. B 【点拨】由题意,得四边形 ACC'A'为平行四边形, .∴AC= 2AB. ∴ 平行四边形 ACC'A'的面积=故选 B.
8. C 【点拨】如图,过点P作PQ⊥x轴于点 Q.
∵OP∥AB,∴∠CAB=∠CPO,∠ABC=∠COP.∴△OCP∽△BCA.∴CP:AC = OC :BC =1:2.
∵∠AOC=∠AQP=90°,∴CO∥PQ.∴OQ:AO=CP:AC=1:2.∵P(1,1),∴PQ=OQ=1.∴AO=
9.64 【点拨】如图,连接AB,CD,过点 A 作AE⊥CD于E,过点B作BF⊥CD于F.
∵AB∥EF,AE∥BF,∴四边形 ABFE 是平行四边形.
∵∠AEF = 90°,∴四边形 AEFB 是矩形,∴EF=AB=10 cm,
∵AE∥PC,∴∠PCA =∠CAE=30°,∴CE= AC·sin30°=27cm,同理可得DF= 27 cm,
∴CD= CE + EF+DF=27+10+27=64(cm).
10.【解】(1)∵山坡②的坡比i=1:1,∴CN=BN.
∴∠BCN=45°.∴∠ACB=180°-30°-45°=105°.
(2)在 Rt△ACM 中,∠AMC =90°,∠ACM=30°,AM=0.6千米,∴AC=2AM=1.2 千米.
在 Rt△BCN中,∠BNC=90°,∠BCN=45°,CN= =千米,∴ 千米.
∴AC+BC=1.2+2=3.2(千米).
答:在此过程中该登山运动爱好者走过的路程为3.2千米.
【点拨】如图,过点D.A作AD⊥BC 交BC 的延长线于点D,
∵AD⊥BC,∴∠ADB=90°.
∵∠CAB=15°,∠B=30°,∴∠DCA=30°+15°=45°,AB=2AD,∴AD=CD.
在Rt△ADC中,·
12.【解】(1)
(2)过点A作AE⊥BC 于点E.
设BC=8x,AB=5x,
解得 (负值舍去),
∴△ABC的周长为
13.【解】如图,过点 B作 BD⊥AE于点 D,延长BC 交 AE于点 N,过点 C作 CM⊥AE于点M.
在Rt△ABD中,∠A=60°,AB=16 cm,
∵∠BAE=60°,∠ABC=50°,∴∠ANB=70°.
在 Rt△NBD中,
∴CN≈14.72-8 =6.72(cm).
在 Rt△CNM中,∠CNM=70°,CN≈6.72 cm,
答:点C到AE 的距离为6.3 cm.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
