辽宁省沈阳市五校协作体2022-2023学年高二下学期期末联考数学试题(Word含答案)
文档属性
| 名称 | 辽宁省沈阳市五校协作体2022-2023学年高二下学期期末联考数学试题(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 459.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 21:56:39 | ||
图片预览




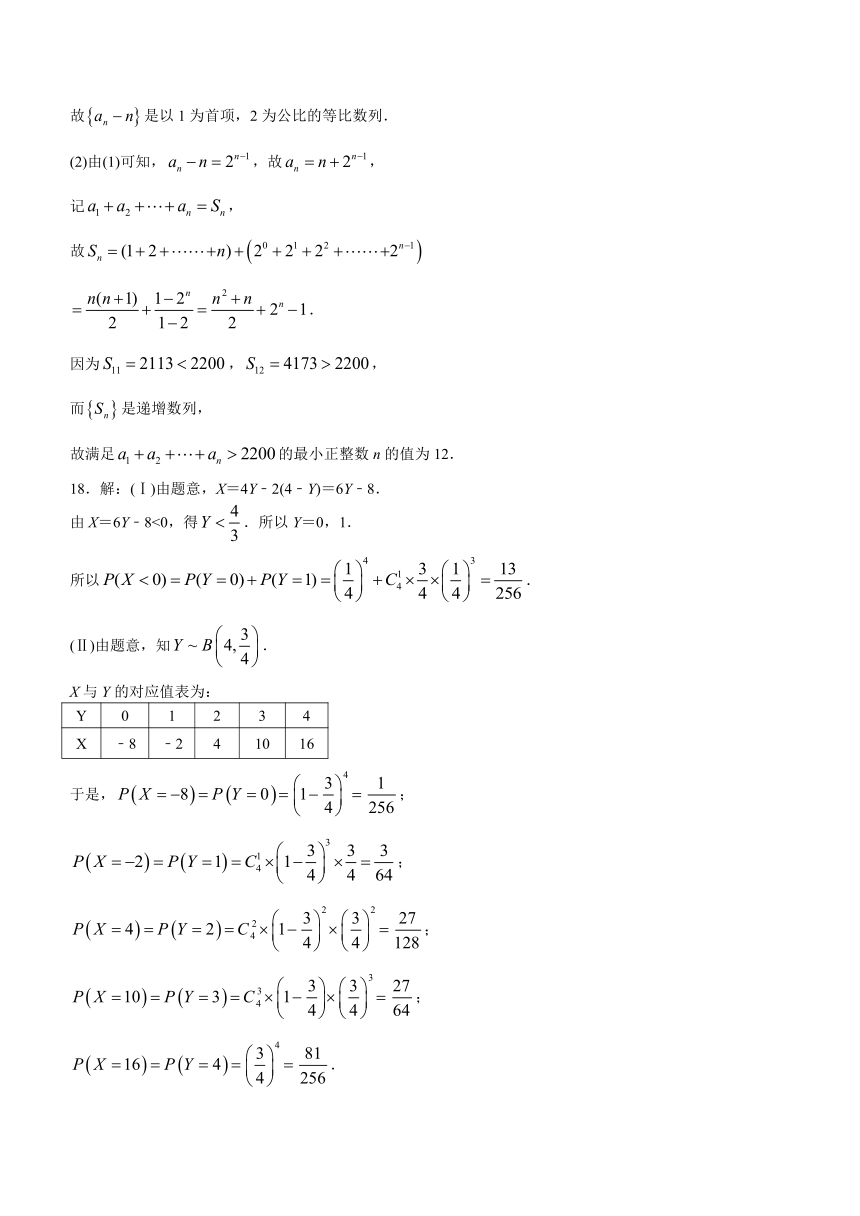
文档简介
2022﹣2023学年度(下)沈阳市五校协作体期末考试
高二年级数学试卷
考试时间:120分钟 分数:150分
试卷说明:试卷共2部分:第一部分:选择题型(1﹣12题,60分)第二部分:非选择题型(13﹣22题,共90分)。
第Ⅰ卷(选择题共60分)
一、单选题(本大题共8小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1.已知集合,集合,若“x∈A”是“x∈B”的充分不必要条件,则实数a的取值范围( )
A. B. C. D.
2.某大学推荐7名男生和5名女生参加某企业的暑期兼职,该企业欲在这12人中随机挑选3人从事产品的销售工作,记抽到的男生人数为X,则E(X)=( )
A.2 B. C. D.
3.若函数f(x)=xlnx﹣a有两个零点,则实数a的取值范围是( )
A. B. C. D.
4.设d,Sn分别为等差数列的公差与前n项和,若,则下列论断中正确的有( )
A.当n=15时,Sn取最大值 B.当n=30时,Sn=1
C.当d>0时, D.当d<0时,
5.某实验室针对某种新型病毒研发了一种疫苗,并在500名志愿者身上进行了人体注射实验,发现注射疫苗的志愿者均产生了稳定的免疫应答.若这些志愿者的某免疫反应蛋白M的数值X(单位:mg/L)近似服从正态分布N(15,σ2),且X在区间(10,20)内的人数占总人数的,则这些志愿者中免疫反应蛋白M的数值X不低于20的人数大约为( )
A.30 B.60 C.70 D.140
6.设a>0,b>0,a+b=1,则下列说法错误的是( )
A.ab的最大值为 B.a2+b2的最小值为
C.的最小值为9 D.的最小值为
7.已知数列的各项均为正数,且,对于任意的n∈N*,均有,.若在数列中去掉的项,余下的项组成数列,则( )
A.12010 B.12100 C.11200 D.11202
8.已知,,,则( )
A.a二、多选题(本大题共4小题,共20分。在每小题有多项符合题目要求)
9.下列说法正确的是( )
A.若函数f(x)的定义域为[0,2],则函数f(2x)的定义域为[0,4]
B.图象关于点(﹣2,1)成中心对称
C.的最大值为
D.幂函数在(0,+∞)上为减函数,则m的值为1
10.有3台车床加工同一型号的零件,第1,2,3台加工的次品率分别为6%,5%,4%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数的比为5:6:9,现任取一个零件,记事件Ai=“零件为第i台车床加工”(i=1,2,3),事件B=“零件为次品”,则( )
A. B. C.P(B)=0.048 D.
11.在数列中,,且对任意不小于2的正整数n,恒成立,则下列结论正确的是( )
A. B.
C.成等比数列 D.
12.定义在R上的函数f(x)与g(x)的导函数分别为和,若,,且g(x+2)为奇函数,则下列说法中一定正确的是( )
A.g(2)=0 B.函数关于x=2对称
C.函数f(x)是周期函数 D.
第Ⅱ卷(非选择题共90分)
三、填空题(本大题共4小题,共20分)
13.函数的值域为______.
14.已知函数f(x)满足f(x+2)=2f(x),且当x∈[8,10]时,f(x)=﹣(x﹣8)(x﹣10).若f(x)=t,x∈[0,10]恰有6个解,则t的取值范围______.
15.设定义在(0,+∞)上的函数f(x)满足,则函数在定义域内是______(填“增”或“减”)函数;若,,则x的最小值为______.
16.已知数列满足,是数列的前n项和且,则______.
四、解答题(本大题共6小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17.(本小题10分)
已知数列满足,且,数列是公差为﹣1的等差数列.
(1)探究:数列是等差数列还是等比数列,并说明理由;
(2)求使得成立的最小正整数n的值.
18.(本小题12分)
某校组织数学知识竞赛活动,比赛共4道必答题,答对一题得4分,答错一题扣2分.学生甲参加了这次活动,假设每道题甲能答对的概率都是,且各题答对与否互不影响.设甲答对的题数为Y,甲做完4道题后的总得分为X.
(1)试建立X关于Y的函数关系式,并求P(X<0);
(2)求X的分布列及E(X).
19.(本小题12分)
已知函数.
(1)求函数f(x)在x=1处的切线方程;
(2)若不等式f(x)≥ax(a∈R)恒成立,求实数a的取值范围.
20.(本小题12分)
区教育局准备组织一次安全知识竞赛.某校为了选拔学生参赛,按性别采用分层抽样的方法抽取200名学生进行安全知识测试,记A=“性别为男”,B=“得分超过85分”,且,,.
(1)完成下列2×2列联表,并根据小概率值α=0.001的独立性检验,能否推断该校学生了解安全知识的程度与性别有关?
性别 了解安全知识的程度 合计
得分不超过85分的人数 得分超过85的人数
男
女
合计
(2)学校准备分别选取参与测试的男生和女生前两名学生代表学校参加区级别的竞赛,已知男生获奖的概率为,女生获奖的概率为,记该校获奖的人数为X,求X的分布列与数学期望.
下表是独立性检验中几个常用的小概率值和相应的临界值.
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
21.(本小题12分)
已知等差数列满足,其中Sn为的前n项和,递增的等比数列满足:,且成等差数列.
(1)求数列、的通项公式;
(2)设的前n项和为Tn,求Tn
(3)设,的前n项和为An,若恒成立,求实数λ的最大值.
22.(本小题12分)
已知函数.
(1)若f(x)有两个不同的极值点,,求实数a的取值范围;
(2)在(1)的条件下,求证:.
2022—2023学年度(下)沈阳市五校协作体期末
高二年级数学学科答案
一、选择题;
1.A 2.B 3.C 4.C 5.B 6.D 7.D 8.A
9.BD 10.ACD 11.BCD 12.ACD
二、填空题:
13. 14. 15.增 16.
三、解答题;
17.(1)依题意,,
当n=1吋,,即,
故,则,
故,
故,
而,
故是以1为首项,2为公比的等比数列.
(2)由(1)可知,,故,
记,
故
.
因为,,
而是递增数列,
故满足的最小正整数n的值为12.
18.解:(Ⅰ)由题意,X=4Y﹣2(4﹣Y)=6Y﹣8.
由X=6Y﹣8<0,得.所以Y=0,1.
所以.
(Ⅱ)由题意,知.
X与Y的对应值表为:
Y 0 1 2 3 4
X ﹣8 ﹣2 4 10 16
于是,;
;
;
;
.
X ﹣8 ﹣2 4 10 16
P
19.解:(1)∵,
∴,
∴,,
∴f(x)的图象在x=1处的切线方程为y﹣(e﹣1)=(2e﹣1)(x﹣1),即y=(2e﹣1)x﹣e.
(2)由题意得,因为函数,
故有:f(x)≥ax,x>0,等价转化为:
即,整理得:在x>0时恒成立,所以,
令,则:,
令,则:,∴函数φ(x)在x>0时单调递增,
∵,,
∴,使得,
∴当时,φ(x)<0,即,h(x)函数单调递减,
当时,φ(x)>0,即,h(x)函数单调递增,
故,
由,得,
在中,,
当x∈(0,1)时,,∴函数在(0,1)上单调递增,
∴,即:与,
,
∴a≤1,即实数a的取值范围为(﹣∞,1]
20.解:(1)因为,
,,,
所以,即,
所以,,
所以200人中男生有120人,女生有80人,测试成绩超过85分的有150人,其中男生100人,女生50人.2×2列联表如下:
性别 了解安全知识的程度 合计
得分不超过85分的人数 得分超过85的人数
男 20 100 120
女 30 50 80
合计 50 150 200
零假设为:该校学生了解安全知识的程度与性别没有关联.
根据列联表中的数据,
经计算得到
根据小概率值α=0.001的独立性检验,可以推断H0不成立,即认为了解安全知识的程度与性别有关,此推断犯错误的概率不大于0.001
(2)X可能取0,1,2,3,4.
;
;
;
.
所以X的分布列为
X 0 1 2 3 4
P
所以.
21.解:(1)设等差数列的公差为d,∵,
∴,∴,d=2,
∴.
设等比数列公比为q(其中q>0),因为b1=1,
由,可得,解得q=3或﹣1(舍去);
∴数列的通项公式为.
(2)由(1)得,
则①,
②,
由①﹣②得,
则,
所以,
(3)由(1)可知,,
则,
∴
∵恒成立,∴恒成立,
∵单调递增,∴n=1时,,
∴,∴的最大值为.
22.解:(1)由得,
因为f(x)有两个不同的极值点,,
则有两个不同的零点,
即方程有两个不同的实根,
即直线y=a与的图象有两个不同的交点,
设,则,
当x∈(﹣∞,1)时,,g(x)单调递增,
且g(x)的取值范围是;
当x∈(1,+∞)时,,g(x)单调递减,
且g(x)的取值范围是,
所以当时,直线y=a与的图象有两个不同的交点,f(x)有两个不同的极值点,,
故实数a的取值范围是;
(2)由(1)知,设,则,
由得,
即,所以要证,只需证,
即证,即证,
设(t<0),即证,即证,
设,则,
所以h(t)在(﹣∞,0)是增函数,h(t)所以,
从而有.
高二年级数学试卷
考试时间:120分钟 分数:150分
试卷说明:试卷共2部分:第一部分:选择题型(1﹣12题,60分)第二部分:非选择题型(13﹣22题,共90分)。
第Ⅰ卷(选择题共60分)
一、单选题(本大题共8小题,共40分。在每小题列出的选项中,选出符合题目的一项)
1.已知集合,集合,若“x∈A”是“x∈B”的充分不必要条件,则实数a的取值范围( )
A. B. C. D.
2.某大学推荐7名男生和5名女生参加某企业的暑期兼职,该企业欲在这12人中随机挑选3人从事产品的销售工作,记抽到的男生人数为X,则E(X)=( )
A.2 B. C. D.
3.若函数f(x)=xlnx﹣a有两个零点,则实数a的取值范围是( )
A. B. C. D.
4.设d,Sn分别为等差数列的公差与前n项和,若,则下列论断中正确的有( )
A.当n=15时,Sn取最大值 B.当n=30时,Sn=1
C.当d>0时, D.当d<0时,
5.某实验室针对某种新型病毒研发了一种疫苗,并在500名志愿者身上进行了人体注射实验,发现注射疫苗的志愿者均产生了稳定的免疫应答.若这些志愿者的某免疫反应蛋白M的数值X(单位:mg/L)近似服从正态分布N(15,σ2),且X在区间(10,20)内的人数占总人数的,则这些志愿者中免疫反应蛋白M的数值X不低于20的人数大约为( )
A.30 B.60 C.70 D.140
6.设a>0,b>0,a+b=1,则下列说法错误的是( )
A.ab的最大值为 B.a2+b2的最小值为
C.的最小值为9 D.的最小值为
7.已知数列的各项均为正数,且,对于任意的n∈N*,均有,.若在数列中去掉的项,余下的项组成数列,则( )
A.12010 B.12100 C.11200 D.11202
8.已知,,,则( )
A.a
9.下列说法正确的是( )
A.若函数f(x)的定义域为[0,2],则函数f(2x)的定义域为[0,4]
B.图象关于点(﹣2,1)成中心对称
C.的最大值为
D.幂函数在(0,+∞)上为减函数,则m的值为1
10.有3台车床加工同一型号的零件,第1,2,3台加工的次品率分别为6%,5%,4%,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数的比为5:6:9,现任取一个零件,记事件Ai=“零件为第i台车床加工”(i=1,2,3),事件B=“零件为次品”,则( )
A. B. C.P(B)=0.048 D.
11.在数列中,,且对任意不小于2的正整数n,恒成立,则下列结论正确的是( )
A. B.
C.成等比数列 D.
12.定义在R上的函数f(x)与g(x)的导函数分别为和,若,,且g(x+2)为奇函数,则下列说法中一定正确的是( )
A.g(2)=0 B.函数关于x=2对称
C.函数f(x)是周期函数 D.
第Ⅱ卷(非选择题共90分)
三、填空题(本大题共4小题,共20分)
13.函数的值域为______.
14.已知函数f(x)满足f(x+2)=2f(x),且当x∈[8,10]时,f(x)=﹣(x﹣8)(x﹣10).若f(x)=t,x∈[0,10]恰有6个解,则t的取值范围______.
15.设定义在(0,+∞)上的函数f(x)满足,则函数在定义域内是______(填“增”或“减”)函数;若,,则x的最小值为______.
16.已知数列满足,是数列的前n项和且,则______.
四、解答题(本大题共6小题,共72分。解答应写出文字说明,证明过程或演算步骤)
17.(本小题10分)
已知数列满足,且,数列是公差为﹣1的等差数列.
(1)探究:数列是等差数列还是等比数列,并说明理由;
(2)求使得成立的最小正整数n的值.
18.(本小题12分)
某校组织数学知识竞赛活动,比赛共4道必答题,答对一题得4分,答错一题扣2分.学生甲参加了这次活动,假设每道题甲能答对的概率都是,且各题答对与否互不影响.设甲答对的题数为Y,甲做完4道题后的总得分为X.
(1)试建立X关于Y的函数关系式,并求P(X<0);
(2)求X的分布列及E(X).
19.(本小题12分)
已知函数.
(1)求函数f(x)在x=1处的切线方程;
(2)若不等式f(x)≥ax(a∈R)恒成立,求实数a的取值范围.
20.(本小题12分)
区教育局准备组织一次安全知识竞赛.某校为了选拔学生参赛,按性别采用分层抽样的方法抽取200名学生进行安全知识测试,记A=“性别为男”,B=“得分超过85分”,且,,.
(1)完成下列2×2列联表,并根据小概率值α=0.001的独立性检验,能否推断该校学生了解安全知识的程度与性别有关?
性别 了解安全知识的程度 合计
得分不超过85分的人数 得分超过85的人数
男
女
合计
(2)学校准备分别选取参与测试的男生和女生前两名学生代表学校参加区级别的竞赛,已知男生获奖的概率为,女生获奖的概率为,记该校获奖的人数为X,求X的分布列与数学期望.
下表是独立性检验中几个常用的小概率值和相应的临界值.
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
21.(本小题12分)
已知等差数列满足,其中Sn为的前n项和,递增的等比数列满足:,且成等差数列.
(1)求数列、的通项公式;
(2)设的前n项和为Tn,求Tn
(3)设,的前n项和为An,若恒成立,求实数λ的最大值.
22.(本小题12分)
已知函数.
(1)若f(x)有两个不同的极值点,,求实数a的取值范围;
(2)在(1)的条件下,求证:.
2022—2023学年度(下)沈阳市五校协作体期末
高二年级数学学科答案
一、选择题;
1.A 2.B 3.C 4.C 5.B 6.D 7.D 8.A
9.BD 10.ACD 11.BCD 12.ACD
二、填空题:
13. 14. 15.增 16.
三、解答题;
17.(1)依题意,,
当n=1吋,,即,
故,则,
故,
故,
而,
故是以1为首项,2为公比的等比数列.
(2)由(1)可知,,故,
记,
故
.
因为,,
而是递增数列,
故满足的最小正整数n的值为12.
18.解:(Ⅰ)由题意,X=4Y﹣2(4﹣Y)=6Y﹣8.
由X=6Y﹣8<0,得.所以Y=0,1.
所以.
(Ⅱ)由题意,知.
X与Y的对应值表为:
Y 0 1 2 3 4
X ﹣8 ﹣2 4 10 16
于是,;
;
;
;
.
X ﹣8 ﹣2 4 10 16
P
19.解:(1)∵,
∴,
∴,,
∴f(x)的图象在x=1处的切线方程为y﹣(e﹣1)=(2e﹣1)(x﹣1),即y=(2e﹣1)x﹣e.
(2)由题意得,因为函数,
故有:f(x)≥ax,x>0,等价转化为:
即,整理得:在x>0时恒成立,所以,
令,则:,
令,则:,∴函数φ(x)在x>0时单调递增,
∵,,
∴,使得,
∴当时,φ(x)<0,即,h(x)函数单调递减,
当时,φ(x)>0,即,h(x)函数单调递增,
故,
由,得,
在中,,
当x∈(0,1)时,,∴函数在(0,1)上单调递增,
∴,即:与,
,
∴a≤1,即实数a的取值范围为(﹣∞,1]
20.解:(1)因为,
,,,
所以,即,
所以,,
所以200人中男生有120人,女生有80人,测试成绩超过85分的有150人,其中男生100人,女生50人.2×2列联表如下:
性别 了解安全知识的程度 合计
得分不超过85分的人数 得分超过85的人数
男 20 100 120
女 30 50 80
合计 50 150 200
零假设为:该校学生了解安全知识的程度与性别没有关联.
根据列联表中的数据,
经计算得到
根据小概率值α=0.001的独立性检验,可以推断H0不成立,即认为了解安全知识的程度与性别有关,此推断犯错误的概率不大于0.001
(2)X可能取0,1,2,3,4.
;
;
;
.
所以X的分布列为
X 0 1 2 3 4
P
所以.
21.解:(1)设等差数列的公差为d,∵,
∴,∴,d=2,
∴.
设等比数列公比为q(其中q>0),因为b1=1,
由,可得,解得q=3或﹣1(舍去);
∴数列的通项公式为.
(2)由(1)得,
则①,
②,
由①﹣②得,
则,
所以,
(3)由(1)可知,,
则,
∴
∵恒成立,∴恒成立,
∵单调递增,∴n=1时,,
∴,∴的最大值为.
22.解:(1)由得,
因为f(x)有两个不同的极值点,,
则有两个不同的零点,
即方程有两个不同的实根,
即直线y=a与的图象有两个不同的交点,
设,则,
当x∈(﹣∞,1)时,,g(x)单调递增,
且g(x)的取值范围是;
当x∈(1,+∞)时,,g(x)单调递减,
且g(x)的取值范围是,
所以当时,直线y=a与的图象有两个不同的交点,f(x)有两个不同的极值点,,
故实数a的取值范围是;
(2)由(1)知,设,则,
由得,
即,所以要证,只需证,
即证,即证,
设(t<0),即证,即证,
设,则,
所以h(t)在(﹣∞,0)是增函数,h(t)
从而有.
同课章节目录
