2022-2023学年北师大版八年级上学期开学测试题(无答案)
文档属性
| 名称 | 2022-2023学年北师大版八年级上学期开学测试题(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 131.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 00:00:00 | ||
图片预览

文档简介
2022-2023学年北师大版8年级上册开学测练习01
一.选择题(共10小题)
1.下列从左到右的变形,错误的是( )
A.﹣m+n=﹣(m+n) B.﹣a﹣b=﹣(a+b)
C.(m﹣n)3=﹣(n﹣m)3 D.(y﹣x)2=(x﹣y)2
2.下列各组数中不能作为直角三角形的三边长的是( )
A.2,3,4 B.5,12,13 C.6,8,10 D.9,12,15
3.9的平方根是( )
A.3 B.±3 C.± D.±81
4.下列事件中是不可能事件的是( )
A.从一副扑克牌中任抽一张牌恰好是“红桃”
B.在装有白球和黑球的袋中摸球,摸出了红球
C.2022年大年初一早晨艳阳高照
D.从两个班级中任选三名学生,至少有两名学生来自同一个班级
5.如图,直线a,b被直线c所截,下列说法中不正确的是( )
A.∠1与∠2是对顶角 B.∠2与∠5是同位角
C.∠3与∠5是同旁内角 D.∠2与∠4是内错角
第5题图 第7题图 第10题图
6.如果等腰三角形两边长是8cm和4cm,那么它的周长是( )
A.20cm B.16cm C.20cm或16cm D.12cm
7.如图,AB=AC,点D、E分别在AB、AC上,补充一个条件后,仍不能判定△ABE≌△ACD的是( )
A.∠B=∠C B.AD=AE C.BE=CD D.∠AEB=∠ADC
8.下列说法不正确的是( )
A.27的立方根是±3 B.的立方根是 C.16的平方根是±4 D.﹣8的立方根是﹣2
9.已知汽车油箱内有油50L,每行驶100km耗油10L,那么汽车行驶过程中油箱内剩余的油量Q(L)与行驶路程s(km)之间的关系式是( )
A.Q=50 B.Q=50 C.Q=50 D.Q=50
10.如图,已知∠ABC、∠EAC的角平分线BP、AP相交于点P,PM⊥BE,PN⊥BF,垂足分别为从N.现有四个结论:
①CP平分∠ACF;
②∠BPC∠BAC;
③∠APC=90°∠ABC;
④S△APM+S△CPN>S△APC.
其中结论正确的是( )(填写结论的编号)
A.①②③ B.①②③④ C.②③④ D.①③④
二.填空题(共7小题)
11.计算:x8÷x2= .
12.中x的取值范围为 .
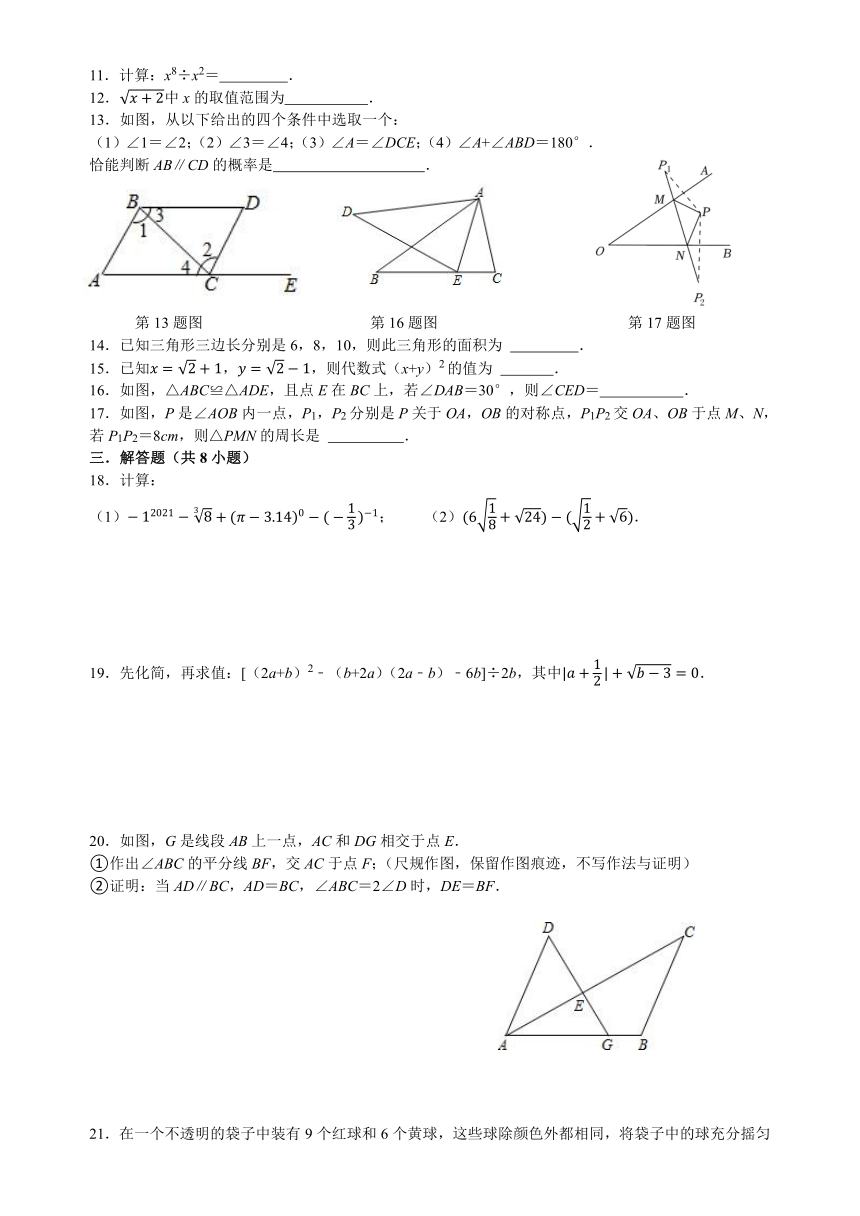
13.如图,从以下给出的四个条件中选取一个:
(1)∠1=∠2;(2)∠3=∠4;(3)∠A=∠DCE;(4)∠A+∠ABD=180°.
恰能判断AB∥CD的概率是 .
第13题图 第16题图 第17题图
14.已知三角形三边长分别是6,8,10,则此三角形的面积为 .
15.已知,,则代数式(x+y)2的值为 .
16.如图,△ABC≌△ADE,且点E在BC上,若∠DAB=30°,则∠CED= .
17.如图,P是∠AOB内一点,P1,P2分别是P关于OA,OB的对称点,P1P2交OA、OB于点M、N,若P1P2=8cm,则△PMN的周长是 .
三.解答题(共8小题)
18.计算:
(1); (2).
先化简,再求值:[(2a+b)2﹣(b+2a)(2a﹣b)﹣6b]÷2b,其中.
20.如图,G是线段AB上一点,AC和DG相交于点E.
①作出∠ABC的平分线BF,交AC于点F;(尺规作图,保留作图痕迹,不写作法与证明)
②证明:当AD∥BC,AD=BC,∠ABC=2∠D时,DE=BF.
21.在一个不透明的袋子中装有9个红球和6个黄球,这些球除颜色外都相同,将袋子中的球充分摇匀后,随机摸出一球.
(1)分别求出摸出的球是红球和黄球的概率.
(2)为了使摸出两种球的概率相同,再放进去7个同样的红球或黄球,那么这7个球中红球和黄球的数量分别应是多少?
22.已知x=1﹣2a,y=a+4.
(1)若x的算术平方根为3,求a的值;
(2)如果一个正数的平方根分别为x,y,求这个正数.
23.如图,在Rt△ABC中,∠C=90°,D是边BC上一点,连结AD并延长至点E,AD=DE,过点E作EF⊥BC于点F,连结BE.
(1)求证:△ADC≌△EDF.
(2)若BE=DE,AC=8,CD=4,求AB的长.
24.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)若DE=a,CD=b,并且,求DB的长度.
25.[问题发现]:如图1,已知△ABC中,∠ACB=90°,AC=BC,点P是线段AB上一点,过点A作AE⊥CP交CP延长线于点E,过点B作BF⊥CP于点F.
(1)若BF=8,AE=3,则EF= ;
(2)在图1中,线段AE、BF、EF有怎样的数量关系?请说明理由.
[拓展应用]:(3)如图2,已知△ABC中,∠ACB=90°,AC=BC,点P是△ABC内部一点,且BP⊥CP,连接AP,若CP=5,求△ACP 的面积.
一.选择题(共10小题)
1.下列从左到右的变形,错误的是( )
A.﹣m+n=﹣(m+n) B.﹣a﹣b=﹣(a+b)
C.(m﹣n)3=﹣(n﹣m)3 D.(y﹣x)2=(x﹣y)2
2.下列各组数中不能作为直角三角形的三边长的是( )
A.2,3,4 B.5,12,13 C.6,8,10 D.9,12,15
3.9的平方根是( )
A.3 B.±3 C.± D.±81
4.下列事件中是不可能事件的是( )
A.从一副扑克牌中任抽一张牌恰好是“红桃”
B.在装有白球和黑球的袋中摸球,摸出了红球
C.2022年大年初一早晨艳阳高照
D.从两个班级中任选三名学生,至少有两名学生来自同一个班级
5.如图,直线a,b被直线c所截,下列说法中不正确的是( )
A.∠1与∠2是对顶角 B.∠2与∠5是同位角
C.∠3与∠5是同旁内角 D.∠2与∠4是内错角
第5题图 第7题图 第10题图
6.如果等腰三角形两边长是8cm和4cm,那么它的周长是( )
A.20cm B.16cm C.20cm或16cm D.12cm
7.如图,AB=AC,点D、E分别在AB、AC上,补充一个条件后,仍不能判定△ABE≌△ACD的是( )
A.∠B=∠C B.AD=AE C.BE=CD D.∠AEB=∠ADC
8.下列说法不正确的是( )
A.27的立方根是±3 B.的立方根是 C.16的平方根是±4 D.﹣8的立方根是﹣2
9.已知汽车油箱内有油50L,每行驶100km耗油10L,那么汽车行驶过程中油箱内剩余的油量Q(L)与行驶路程s(km)之间的关系式是( )
A.Q=50 B.Q=50 C.Q=50 D.Q=50
10.如图,已知∠ABC、∠EAC的角平分线BP、AP相交于点P,PM⊥BE,PN⊥BF,垂足分别为从N.现有四个结论:
①CP平分∠ACF;
②∠BPC∠BAC;
③∠APC=90°∠ABC;
④S△APM+S△CPN>S△APC.
其中结论正确的是( )(填写结论的编号)
A.①②③ B.①②③④ C.②③④ D.①③④
二.填空题(共7小题)
11.计算:x8÷x2= .
12.中x的取值范围为 .
13.如图,从以下给出的四个条件中选取一个:
(1)∠1=∠2;(2)∠3=∠4;(3)∠A=∠DCE;(4)∠A+∠ABD=180°.
恰能判断AB∥CD的概率是 .
第13题图 第16题图 第17题图
14.已知三角形三边长分别是6,8,10,则此三角形的面积为 .
15.已知,,则代数式(x+y)2的值为 .
16.如图,△ABC≌△ADE,且点E在BC上,若∠DAB=30°,则∠CED= .
17.如图,P是∠AOB内一点,P1,P2分别是P关于OA,OB的对称点,P1P2交OA、OB于点M、N,若P1P2=8cm,则△PMN的周长是 .
三.解答题(共8小题)
18.计算:
(1); (2).
先化简,再求值:[(2a+b)2﹣(b+2a)(2a﹣b)﹣6b]÷2b,其中.
20.如图,G是线段AB上一点,AC和DG相交于点E.
①作出∠ABC的平分线BF,交AC于点F;(尺规作图,保留作图痕迹,不写作法与证明)
②证明:当AD∥BC,AD=BC,∠ABC=2∠D时,DE=BF.
21.在一个不透明的袋子中装有9个红球和6个黄球,这些球除颜色外都相同,将袋子中的球充分摇匀后,随机摸出一球.
(1)分别求出摸出的球是红球和黄球的概率.
(2)为了使摸出两种球的概率相同,再放进去7个同样的红球或黄球,那么这7个球中红球和黄球的数量分别应是多少?
22.已知x=1﹣2a,y=a+4.
(1)若x的算术平方根为3,求a的值;
(2)如果一个正数的平方根分别为x,y,求这个正数.
23.如图,在Rt△ABC中,∠C=90°,D是边BC上一点,连结AD并延长至点E,AD=DE,过点E作EF⊥BC于点F,连结BE.
(1)求证:△ADC≌△EDF.
(2)若BE=DE,AC=8,CD=4,求AB的长.
24.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)若DE=a,CD=b,并且,求DB的长度.
25.[问题发现]:如图1,已知△ABC中,∠ACB=90°,AC=BC,点P是线段AB上一点,过点A作AE⊥CP交CP延长线于点E,过点B作BF⊥CP于点F.
(1)若BF=8,AE=3,则EF= ;
(2)在图1中,线段AE、BF、EF有怎样的数量关系?请说明理由.
[拓展应用]:(3)如图2,已知△ABC中,∠ACB=90°,AC=BC,点P是△ABC内部一点,且BP⊥CP,连接AP,若CP=5,求△ACP 的面积.
同课章节目录
