22.2 相似三角形的判定(第二课时)
文档属性
| 名称 | 22.2 相似三角形的判定(第二课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 711.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-13 00:00:00 | ||
图片预览





文档简介
课件12张PPT。相似三角形的判定(第二课时)授课人 张华安地点 城北中学2008—10—16相似三角形的判定(第二课时)授课人 张志龙2014—10—23一、知识回顾1、根据相似多边形的定义,你知道什么样的
两个三角形相似吗?满足
(1)对应角相等 (2)对应边成比例
两个条件的两个三角形是相似三角形.2、请同学们描述相似三角形
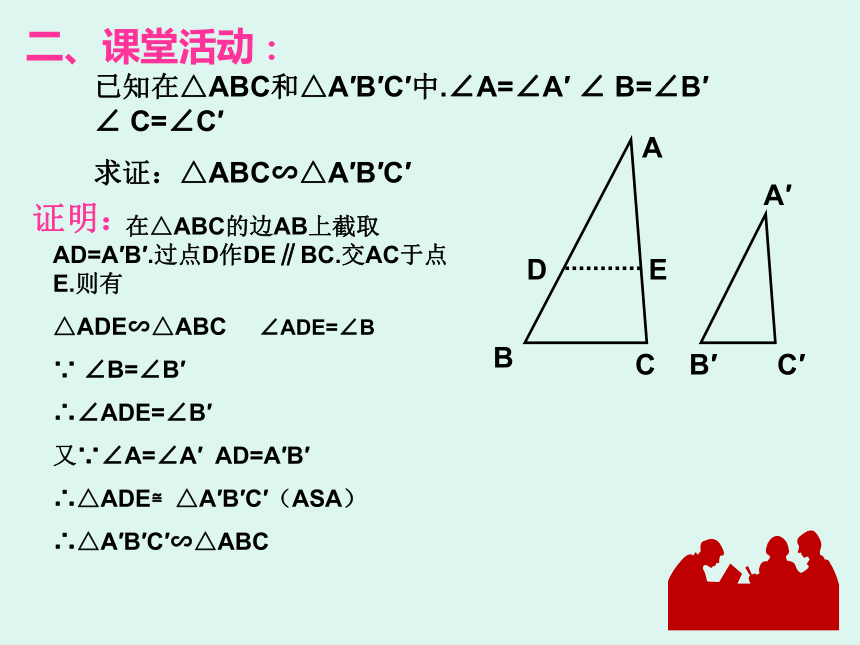
判定定理的预备定理DE∥BC△ADE∽△ ABC二、课堂活动:已知在△ABC和△A′B′C′中.∠A=∠A′ ∠ B=∠B′ ∠ C=∠C′
求证:△ABC∽△A′B′C′DE 在△ABC的边AB上截取AD=A′B′.过点D作DE∥BC.交AC于点E.则有
△ADE∽△ABC ∠ADE=∠B
∵ ∠B=∠B′
∴∠ADE=∠B′
又∵∠A=∠A′ AD=A′B′
∴△ADE≌△A′B′C′(ASA)
∴△A′B′C′∽△ABC证明:由上面的数学活动我们可以得到判定三角形相似的定理定理1:
如果一个三角形的两个角分别与另一个三角形的两个角对应相等.那么这两个三角形相似.
(可简单说成:两个角对应相等的两个三角形相似)想一想:1、△ABC和△A′B′C′中∠A=80°、∠B=40°、∠A=80°、∠C=60°.那么这两个三角形相似吗?
2、等边三角形都相似吗?
3、一个锐角对应相等的两个直角三角形相似吗?
4、有一个内角对应相等的两个等腰三角形相似吗?
5、各有一个内角为100°的两个等腰三角形相似吗?练一练:写出图中的相似三角形:(1)条件: DE∥BC
EF∥AB(2)条件
∠A=36°
AB=AC
BD平分∠ABC(3)条件
∠ACB=90°
CD⊥AB于D△ADE∽△ABC∽△EFC△ABC∽△BDC△ACB∽△ADC∽△CDB例题欣赏:如图C是线段BD上的一点,AB⊥BD.ED⊥BD.AC⊥EC
求证:△ABC∽△CDEE证明:
∵AB⊥BD、ED⊥BD
∴∠ABC=∠CDE=90°
∴∠1+∠A=90°
∵AC⊥EC
∴∠1+∠2=90°
∴∠A=∠2
∴△ABC∽△CDE能力与提高如图所示:已知Rt △ ABC和 Rt △ DEF不相似
其中C、F为直角.能否将每个三角形分别分成两个三角形,使△ ABC所分成的两个三角形与△ DEF所分成的两个三角形分别对应相似?
请设计出一种分割方案12NM方法:在△ABC中,作∠1=∠E,交AB于点N,在△DEF中,作∠2=∠B
FM交DE于点M
则△ANC∽△FME、△BCN∽△FDM 在△ACN和△FME中,
∵∠1=∠E ∠ B=∠2
∴△CAN∽△EFM∵∠ACB=∠DFE=90° ∠ A+∠B=90° ∠D+∠E=90°又∵∠1+∠NCB=90° ∠2+∠EFM=90° ∴∠D=∠NCB ∠ B=∠2∴△BCN∽△FDM∴直线CN、FM就是所求的分割线证明:课堂小结:请同学们再回顾一下我们这节课学习了哪些知识和方法?作业:
P85
习题22.2 第2题(并说明理由)课后预习:
定理2和定理3
两个三角形相似吗?满足
(1)对应角相等 (2)对应边成比例
两个条件的两个三角形是相似三角形.2、请同学们描述相似三角形
判定定理的预备定理DE∥BC△ADE∽△ ABC二、课堂活动:已知在△ABC和△A′B′C′中.∠A=∠A′ ∠ B=∠B′ ∠ C=∠C′
求证:△ABC∽△A′B′C′DE 在△ABC的边AB上截取AD=A′B′.过点D作DE∥BC.交AC于点E.则有
△ADE∽△ABC ∠ADE=∠B
∵ ∠B=∠B′
∴∠ADE=∠B′
又∵∠A=∠A′ AD=A′B′
∴△ADE≌△A′B′C′(ASA)
∴△A′B′C′∽△ABC证明:由上面的数学活动我们可以得到判定三角形相似的定理定理1:
如果一个三角形的两个角分别与另一个三角形的两个角对应相等.那么这两个三角形相似.
(可简单说成:两个角对应相等的两个三角形相似)想一想:1、△ABC和△A′B′C′中∠A=80°、∠B=40°、∠A=80°、∠C=60°.那么这两个三角形相似吗?
2、等边三角形都相似吗?
3、一个锐角对应相等的两个直角三角形相似吗?
4、有一个内角对应相等的两个等腰三角形相似吗?
5、各有一个内角为100°的两个等腰三角形相似吗?练一练:写出图中的相似三角形:(1)条件: DE∥BC
EF∥AB(2)条件
∠A=36°
AB=AC
BD平分∠ABC(3)条件
∠ACB=90°
CD⊥AB于D△ADE∽△ABC∽△EFC△ABC∽△BDC△ACB∽△ADC∽△CDB例题欣赏:如图C是线段BD上的一点,AB⊥BD.ED⊥BD.AC⊥EC
求证:△ABC∽△CDEE证明:
∵AB⊥BD、ED⊥BD
∴∠ABC=∠CDE=90°
∴∠1+∠A=90°
∵AC⊥EC
∴∠1+∠2=90°
∴∠A=∠2
∴△ABC∽△CDE能力与提高如图所示:已知Rt △ ABC和 Rt △ DEF不相似
其中C、F为直角.能否将每个三角形分别分成两个三角形,使△ ABC所分成的两个三角形与△ DEF所分成的两个三角形分别对应相似?
请设计出一种分割方案12NM方法:在△ABC中,作∠1=∠E,交AB于点N,在△DEF中,作∠2=∠B
FM交DE于点M
则△ANC∽△FME、△BCN∽△FDM 在△ACN和△FME中,
∵∠1=∠E ∠ B=∠2
∴△CAN∽△EFM∵∠ACB=∠DFE=90° ∠ A+∠B=90° ∠D+∠E=90°又∵∠1+∠NCB=90° ∠2+∠EFM=90° ∴∠D=∠NCB ∠ B=∠2∴△BCN∽△FDM∴直线CN、FM就是所求的分割线证明:课堂小结:请同学们再回顾一下我们这节课学习了哪些知识和方法?作业:
P85
习题22.2 第2题(并说明理由)课后预习:
定理2和定理3
