三角形的中位线[下学期]
图片预览



文档简介
课件22张PPT。 向参加这此活动的评委、听课的老师们、同学们表示忠心的感谢,谢谢大家!预祝我们合作愉快! 平顶山市第二十六中学
授课人:慕海军幻灯片 4三角形的中位线平顶山市第二十六中学
制作:慕海军上课
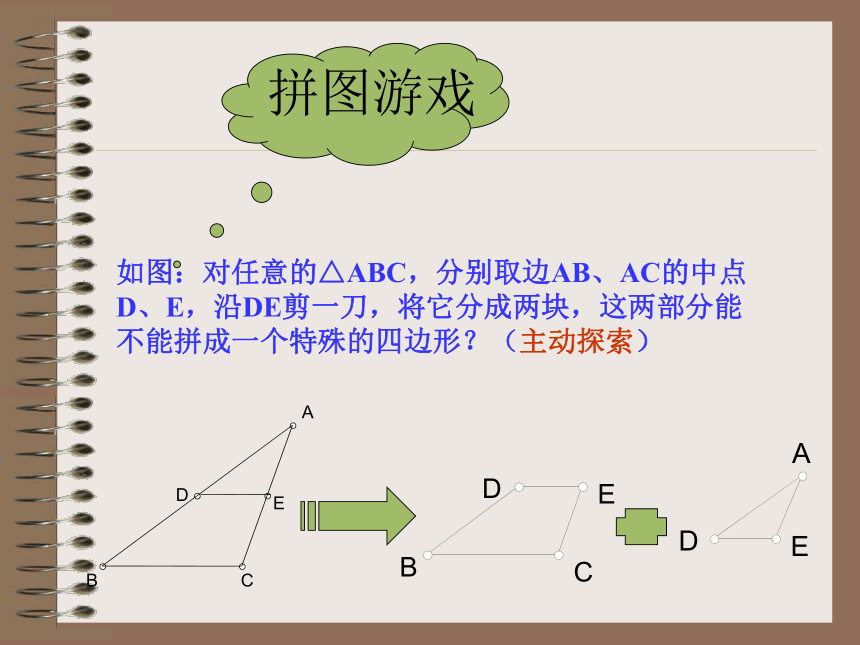
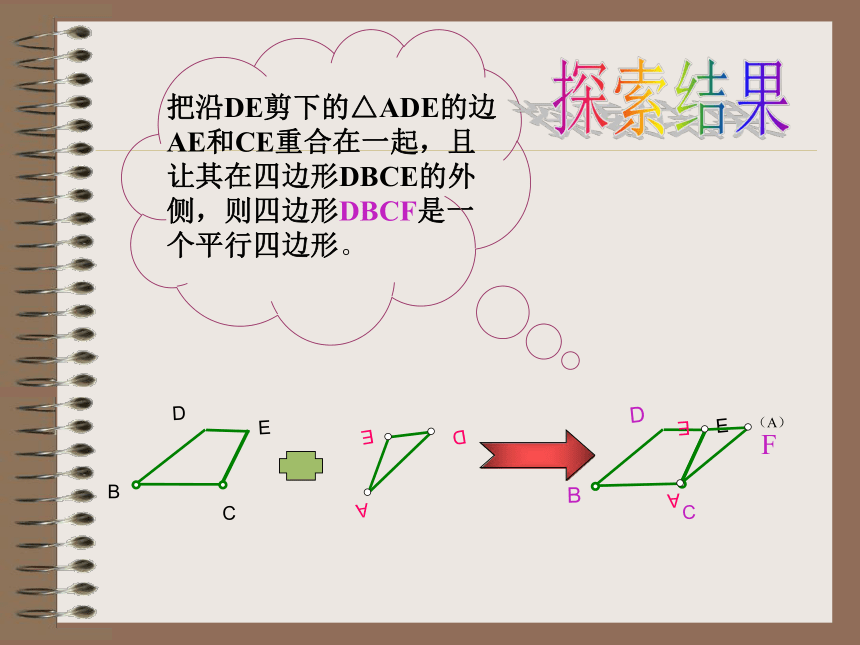
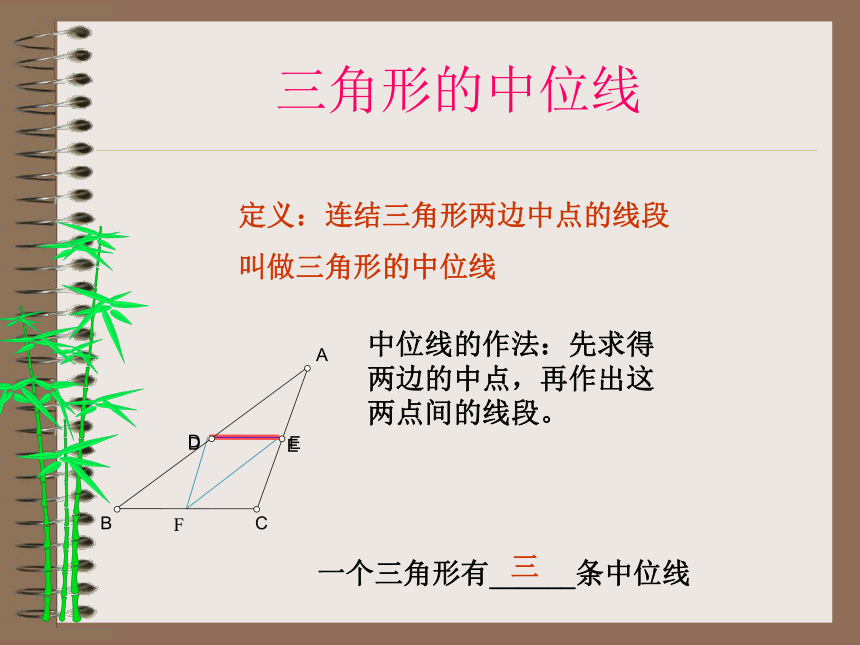
三角形中位线练习与巩固下课ABC如图:对任意的△ABC,分别取边AB、AC的中点D、E,沿DE剪一刀,将它分成两块,这两部分能不能拼成一个特殊的四边形?(主动探索)探索结果三角形的中位线定义:连结三角形两边中点的线段
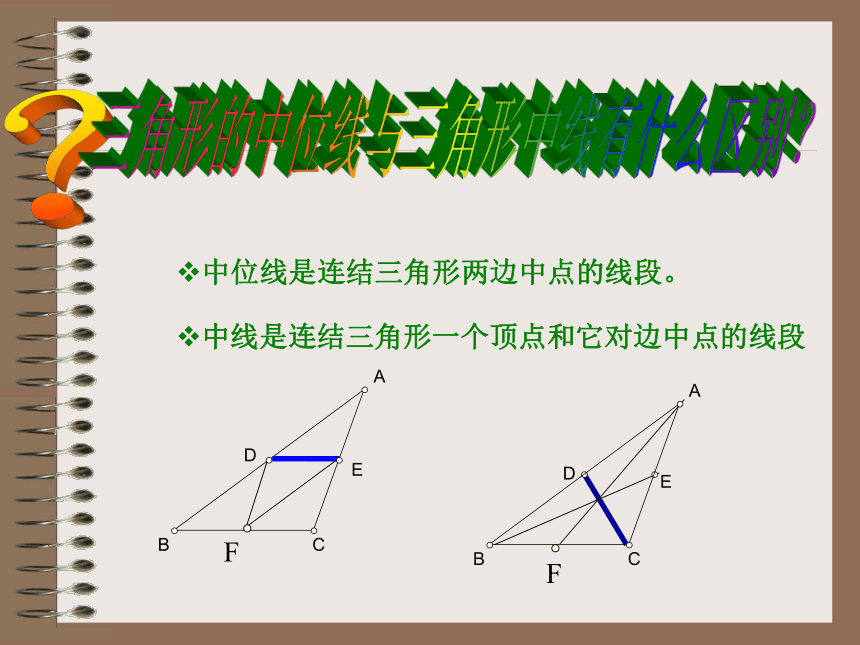
叫做三角形的中位线DE一个三角形有______条中位线三中位线的作法:先求得两边的中点,再作出这两点间的线段。F中位线是连结三角形两边中点的线段。中线是连结三角形一个顶点和它对边中点的线段 从位置和数量关系上看,中位线与第三边之间有怎样的关系?(请大家认真探索,用一句话把它们的关系表示出来。)?主动探索猜想结果:三角形的中位线平行于第三边,并且等于它的一半。证明几何中的文字命题的一般步骤:1、根据题意,画出图形;2、根据题设、结论,结合图形,写出已知和求证;3、经过分析,找出由已知推出求证的途径,写出证明过程。想一想证法一:
证明:延长DE到点F,使EF=DE,2连结CF,1幻灯片13幻灯片 14幻灯片 15 F幻灯片 12幻灯片 14幻灯片 15证法三:ABCDEF1243幻灯片 12幻灯片 13幻灯片 15如图,已知D、E、F分别是△ABC的三边的AB、BC、CA中点。
1、若AB=8cm,求EF的长。
2、若DF=5cm ,求BC的长
3、若G、H分别是BD、BE的中点,求证:GH∥AC练习(基本应用 )(2)∵D、F分别是AB、AC的中点∴ BC=2DF=2 ×5=10cm (3)∵ GH分别 是BD、BE的中点∴ GH∥DE,
同理DE∥AC。
∴ AC∥GH例题1.
求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形。已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH
是平行四边形理解应用(深化提高 )推理论证例题2。当四边形的两条对角线相等或互相垂直时,顺次连结四边中点得到的四边形又是怎样的四边形呢?思考对角线相等时对角线垂直时(变式练习) 菱形 矩形3、顺次连结矩形的各边中点所得的四边形______2、顺次连结平行四边形的各边中点所得的四边形是___________1、顺次连结对角线互相垂直且相等的四边形的各边中点所所得的四边形是________练习讲评、巩固新知正方形平行四边形菱形4、顺次连结菱形的各边中点所得的四边形是______矩形5、顺次连结正方形的各边中点所得的四边形是______正方形6、顺次连结等腰梯形的各边中点所得的四边形____菱形(辩析论证) (八)布置作业
书面作业:
课本第188页第4、6两题
?谢谢指导,敬请指正!返回
授课人:慕海军幻灯片 4三角形的中位线平顶山市第二十六中学
制作:慕海军上课
三角形中位线练习与巩固下课ABC如图:对任意的△ABC,分别取边AB、AC的中点D、E,沿DE剪一刀,将它分成两块,这两部分能不能拼成一个特殊的四边形?(主动探索)探索结果三角形的中位线定义:连结三角形两边中点的线段
叫做三角形的中位线DE一个三角形有______条中位线三中位线的作法:先求得两边的中点,再作出这两点间的线段。F中位线是连结三角形两边中点的线段。中线是连结三角形一个顶点和它对边中点的线段 从位置和数量关系上看,中位线与第三边之间有怎样的关系?(请大家认真探索,用一句话把它们的关系表示出来。)?主动探索猜想结果:三角形的中位线平行于第三边,并且等于它的一半。证明几何中的文字命题的一般步骤:1、根据题意,画出图形;2、根据题设、结论,结合图形,写出已知和求证;3、经过分析,找出由已知推出求证的途径,写出证明过程。想一想证法一:
证明:延长DE到点F,使EF=DE,2连结CF,1幻灯片13幻灯片 14幻灯片 15 F幻灯片 12幻灯片 14幻灯片 15证法三:ABCDEF1243幻灯片 12幻灯片 13幻灯片 15如图,已知D、E、F分别是△ABC的三边的AB、BC、CA中点。
1、若AB=8cm,求EF的长。
2、若DF=5cm ,求BC的长
3、若G、H分别是BD、BE的中点,求证:GH∥AC练习(基本应用 )(2)∵D、F分别是AB、AC的中点∴ BC=2DF=2 ×5=10cm (3)∵ GH分别 是BD、BE的中点∴ GH∥DE,
同理DE∥AC。
∴ AC∥GH例题1.
求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形。已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。求证:四边形EFGH
是平行四边形理解应用(深化提高 )推理论证例题2。当四边形的两条对角线相等或互相垂直时,顺次连结四边中点得到的四边形又是怎样的四边形呢?思考对角线相等时对角线垂直时(变式练习) 菱形 矩形3、顺次连结矩形的各边中点所得的四边形______2、顺次连结平行四边形的各边中点所得的四边形是___________1、顺次连结对角线互相垂直且相等的四边形的各边中点所所得的四边形是________练习讲评、巩固新知正方形平行四边形菱形4、顺次连结菱形的各边中点所得的四边形是______矩形5、顺次连结正方形的各边中点所得的四边形是______正方形6、顺次连结等腰梯形的各边中点所得的四边形____菱形(辩析论证) (八)布置作业
书面作业:
课本第188页第4、6两题
?谢谢指导,敬请指正!返回
