角平分线的性质[上学期]
文档属性
| 名称 | 角平分线的性质[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 498.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-11-20 10:25:00 | ||
图片预览




文档简介
(共19张PPT)
荔城區,岱峰中學 數學組
回憶角平分線的定义
怎樣得出角平分線?
學生試驗:
1,通過折紙的方法作角的
平分線
2,利用简易平分角的仪器
驶向胜利的彼岸
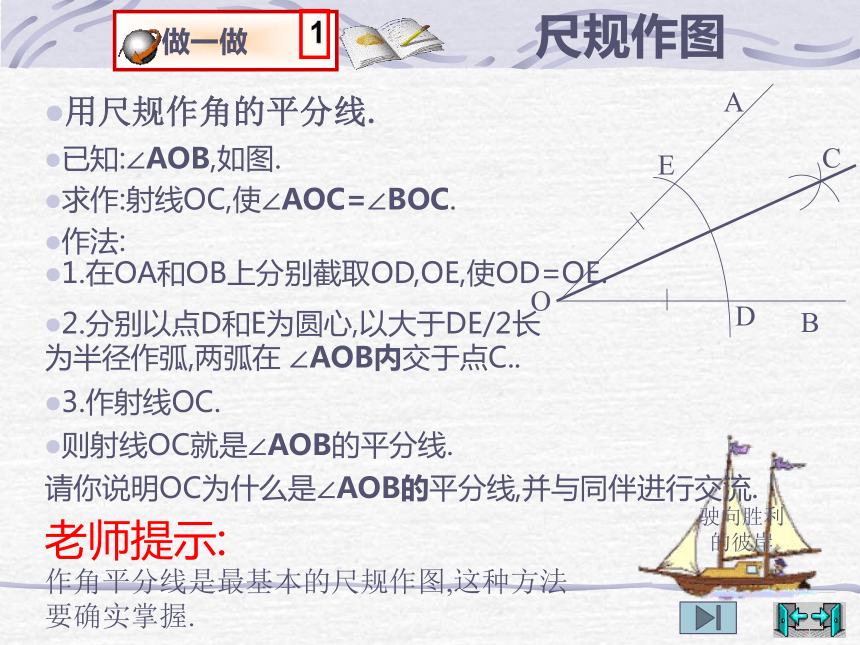
尺规作图
做一做
1
已知:∠AOB,如图.
求作:射线OC,使∠AOC=∠BOC.
作法:
用尺规作角的平分线.
1.在OA和OB上分别截取OD,OE,使OD=OE.
2.分别以点D和E为圆心,以大于DE/2长为半径作弧,两弧在 ∠AOB内交于点C..
3.作射线OC.
请你说明OC为什么是∠AOB的平分线,并与同伴进行交流.
老师提示:
作角平分线是最基本的尺规作图,这种方法要确实掌握.
A
B
O
C
则射线OC就是∠AOB的平分线.
D
E
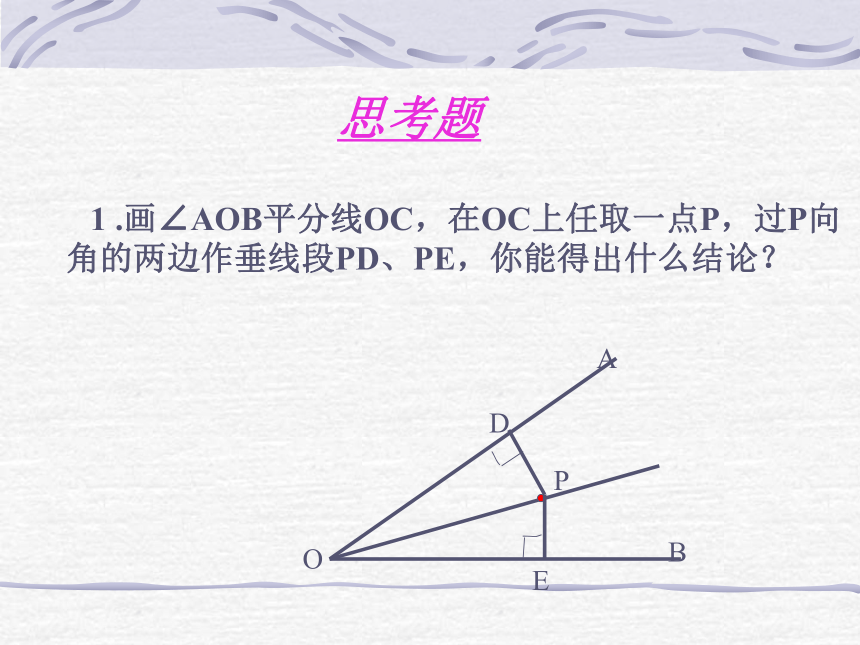
1 .画∠AOB平分线OC,在OC上任取一点P,过P向角的两边作垂线段PD、PE,你能得出什么结论?
思考题
A
O
B
P
E
D
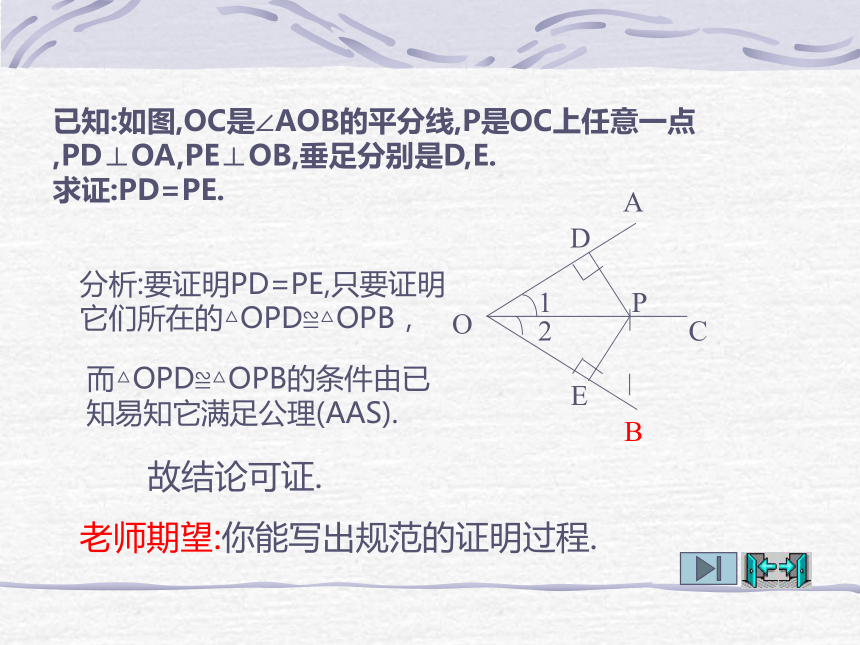
已知:如图,OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E.
求证:PD=PE.
而△OPD≌△OPB的条件由已知易知它满足公理(AAS).
故结论可证.
老师期望:你能写出规范的证明过程.
分析:要证明PD=PE,只要证明它们所在的△OPD≌△OPB,
O
C
B
1
A
2
P
D
E
命题:在角平分线上的点到角的两边的距离相等
题设:一个点在一个角的平分线上
结论:它到角的两边的距离相等
已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E.
求证:PD=PE.
A
O
B
P
E
D
对照证明过程
证明: ∵ PD⊥OA,PE⊥OB
∴ ∠ODP= ∠OEP=90°
在Rt△ODP和Rt △OEP中
∠ODP= ∠OEP
∠1= ∠2
OP=OP
∴ Rt△ODP ≌Rt △OEP(AAS)
∴PD=PE
A
O
B
P
E
D
角平分线的性质
定理:在角平分线上的点到角的两边的距离相等
用符号语言表示为:
A
O
B
P
E
D
1
2
∵∠1= ∠2
PD ⊥OA ,PE ⊥OB
∴PD=PE.
练一练
填空:
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
A
C
D
E
B
1
2
DC=DE
在角平分线上的点到角的两边的距离相等
思考:美梦成真
2.如图,一目标在S区,使它到公路,
铁路距离相等,离公路与铁路的
交叉处500m.在图上标出它的位
置(比例尺 1:20 000).
S
课堂小结
1.角平分线的画法:(尺规作图)
在角平分线上的点到角的两边的距离相等
2.角平分线的性质定理:
在角平分线上的点到角的两边的距离相等.
例 已知:如图,△ABC的角平分线BM、CN相 交于点P.
求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上(已知)
∴PD=PE
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、CA的距离相等
D
E
F
A
B
C
P
M
N
习题13.3
独立作业
3
驶向胜利的彼岸
2.已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC.
老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去.
B
A
E
D
C
F
驶向胜利的彼岸
亲历知识的发生和发展
剪一个三角形纸片通过折叠找出每个角的平分线.
结论:三角形三个角的平分线相交于一点.
老师期望:
你能写出规范的证明过程.
你想证明这个命题吗 你能证明这个命题吗
观察这三条角平分线,你发现了什么
预习 作业
1
亲历知识的发生和发展
利用尺规作出三角形三个角的角平分线.
结论:三角形三个角的角平分线相交于一点.
老师期望:
你能写出规范的证明过程.
你想证明这个命题吗 你能证明这个命题吗
做一做
2
再观察这三条角平分线,你又发现了什么 与同伴交流.
结束寄语
严格性之于数学家,犹如道德之于人.
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.
荔城區,岱峰中學 數學組
回憶角平分線的定义
怎樣得出角平分線?
學生試驗:
1,通過折紙的方法作角的
平分線
2,利用简易平分角的仪器
驶向胜利的彼岸
尺规作图
做一做
1
已知:∠AOB,如图.
求作:射线OC,使∠AOC=∠BOC.
作法:
用尺规作角的平分线.
1.在OA和OB上分别截取OD,OE,使OD=OE.
2.分别以点D和E为圆心,以大于DE/2长为半径作弧,两弧在 ∠AOB内交于点C..
3.作射线OC.
请你说明OC为什么是∠AOB的平分线,并与同伴进行交流.
老师提示:
作角平分线是最基本的尺规作图,这种方法要确实掌握.
A
B
O
C
则射线OC就是∠AOB的平分线.
D
E
1 .画∠AOB平分线OC,在OC上任取一点P,过P向角的两边作垂线段PD、PE,你能得出什么结论?
思考题
A
O
B
P
E
D
已知:如图,OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E.
求证:PD=PE.
而△OPD≌△OPB的条件由已知易知它满足公理(AAS).
故结论可证.
老师期望:你能写出规范的证明过程.
分析:要证明PD=PE,只要证明它们所在的△OPD≌△OPB,
O
C
B
1
A
2
P
D
E
命题:在角平分线上的点到角的两边的距离相等
题设:一个点在一个角的平分线上
结论:它到角的两边的距离相等
已知:OC是∠AOB的平分线,点P在OC上,PD ⊥OA ,PE ⊥OB,垂足分别是D、E.
求证:PD=PE.
A
O
B
P
E
D
对照证明过程
证明: ∵ PD⊥OA,PE⊥OB
∴ ∠ODP= ∠OEP=90°
在Rt△ODP和Rt △OEP中
∠ODP= ∠OEP
∠1= ∠2
OP=OP
∴ Rt△ODP ≌Rt △OEP(AAS)
∴PD=PE
A
O
B
P
E
D
角平分线的性质
定理:在角平分线上的点到角的两边的距离相等
用符号语言表示为:
A
O
B
P
E
D
1
2
∵∠1= ∠2
PD ⊥OA ,PE ⊥OB
∴PD=PE.
练一练
填空:
(1). ∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
A
C
D
E
B
1
2
DC=DE
在角平分线上的点到角的两边的距离相等
思考:美梦成真
2.如图,一目标在S区,使它到公路,
铁路距离相等,离公路与铁路的
交叉处500m.在图上标出它的位
置(比例尺 1:20 000).
S
课堂小结
1.角平分线的画法:(尺规作图)
在角平分线上的点到角的两边的距离相等
2.角平分线的性质定理:
在角平分线上的点到角的两边的距离相等.
例 已知:如图,△ABC的角平分线BM、CN相 交于点P.
求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD 、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F
∵BM是△ABC的角平分线,点P在BM上(已知)
∴PD=PE
(在角平分线上的点到角的两边的距离相等)
同理 PE=PF.
∴ PD=PE=PF.
即点P到边AB、BC、CA的距离相等
D
E
F
A
B
C
P
M
N
习题13.3
独立作业
3
驶向胜利的彼岸
2.已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.
求证:EB=FC.
老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去.
B
A
E
D
C
F
驶向胜利的彼岸
亲历知识的发生和发展
剪一个三角形纸片通过折叠找出每个角的平分线.
结论:三角形三个角的平分线相交于一点.
老师期望:
你能写出规范的证明过程.
你想证明这个命题吗 你能证明这个命题吗
观察这三条角平分线,你发现了什么
预习 作业
1
亲历知识的发生和发展
利用尺规作出三角形三个角的角平分线.
结论:三角形三个角的角平分线相交于一点.
老师期望:
你能写出规范的证明过程.
你想证明这个命题吗 你能证明这个命题吗
做一做
2
再观察这三条角平分线,你又发现了什么 与同伴交流.
结束寄语
严格性之于数学家,犹如道德之于人.
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.
