沪科版八年级数学上册第11.1 平面内点的坐标同步练习 (1-2课时)(含答案)
文档属性
| 名称 | 沪科版八年级数学上册第11.1 平面内点的坐标同步练习 (1-2课时)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 192.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-31 00:00:00 | ||
图片预览




文档简介
11.1 平面内点的坐标
第1课时
一、单选题
1.如图所示四个图形中,是平面直角坐标系的是( )
A. B.
C. D.
2.如图,两坐标轴x轴,y轴把平面直角坐标系分成四部分,则第(3)部分是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列说法中正确的是( )
A.点P(3,2)到x轴距离是3
B.在平面直角坐标系中,点(2,﹣3)和点(﹣2,3)表示同一个点
C.在平面直角坐标系中,第三象限内点的横坐标与纵坐标相等
D.若y=0,则点M(x,y)不属任何一个象限
4.已知点P的坐标为(2m﹣5,m﹣1),且点P到两坐标轴的距离相等,则点P的坐标为( )
A.(﹣1,﹣1) B.(3,3)或(1,﹣1)
C.(﹣1,1)或(3,3) D.(﹣3,﹣4)
5.如果点M(2a+4,a﹣1)在y轴上,那么点M的坐标是( )
A.(﹣2,﹣3) B.(0,﹣3) C.(﹣3,0) D.(0,1)
6.如果点P(a,b)在第三象限,那么点Q(﹣2a+3,b﹣1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.如果点A既在x轴的上方,又在y轴的左边,且距离x轴,y轴分别为5个,4个单位,那么A点的坐标为( )
A.(5,﹣4) B.(4,﹣5) C.(﹣5,4) D.(﹣4,5)
8.下列与(﹣1,5)相连所得的直线与y轴平行的点为( )
A.(1,﹣5) B.(﹣1,2) C.(4,﹣5) D.(2,5)
二、填空题
9.如果点(a,﹣b)在第一象限,那么a 0,b 0(填“>”或“<”).
10.到x轴和y轴的距离都等于2的点有 个,坐标分别为 .
11.如果点P(m﹣3,2+m)在x轴上,那么点P的坐标是 .
12.在平面直角坐标系中,点A的坐标为(a﹣1,a+1),B的坐标为(a+3,a﹣5),若点A在y轴上,则点B的坐标为 .
13.已知点P(a,b)在第三象限,那么点Q(a,﹣b)在第 象限,点M(﹣a,b)在第 象限,点N(﹣a,﹣b)在第 象限.
14.已知A(x+2,2y﹣3)在第二象限,则B(1﹣x,5﹣4y)在第 象限.
三、解答题
15.先画出直角坐标系,再描出下列各点:
A(5,3),B(﹣2,6),C(2,﹣3),D(﹣4,﹣3),E(﹣3,0),F(0,4).
16.在平面直角坐标系中,点A(a﹣2,2a+8),根据下列条件分别求a以及点A的坐标:
(1)当点A在x轴上;
(2)当点A在y轴上.
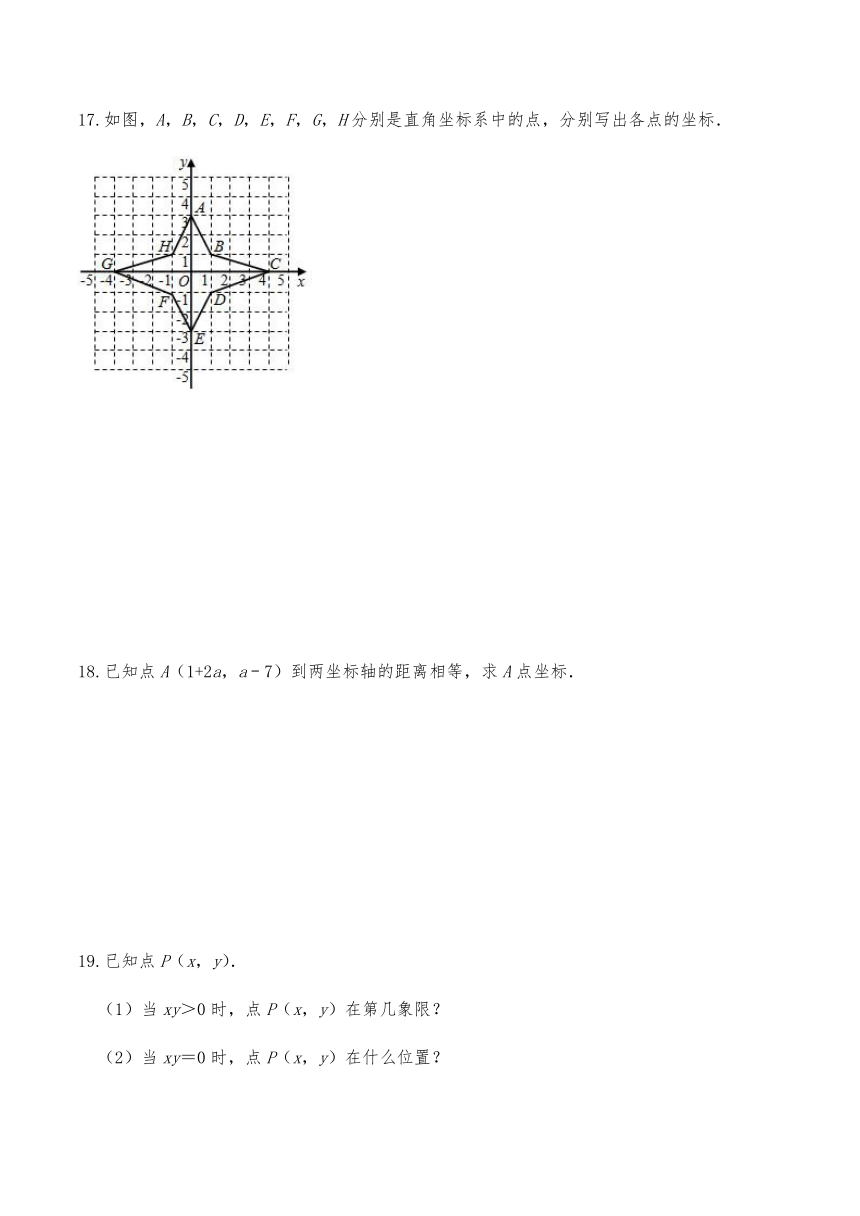
17.如图,A,B,C,D,E,F,G,H分别是直角坐标系中的点,分别写出各点的坐标.
18.已知点A(1+2a,a﹣7)到两坐标轴的距离相等,求A点坐标.
19.已知点P(x,y).
(1)当xy>0时,点P(x,y)在第几象限?
(2)当xy=0时,点P(x,y)在什么位置?
(3)当xy<0时,点P(x,y)在第几象限?
20.若点M(3a﹣9,10﹣2a)在第二象限,且点M到x轴与y轴的距离相等,试求(a+2)2008﹣1的值.
第2课时
一、单选题
1.过点A(﹣3,2)和B(﹣3,5)作直线,则直线AB( )
A.与x轴平行 B.与y轴平行
C.与y轴相交 D.与x轴,y轴均相交
2.下列语句正确的是( )
A.平行于x轴的直线上所有点的横坐标都相同
B.(﹣3,5)与(5,﹣3)表示两个不同的点
C.若点P(a,b)在y轴上,则b=0
3.如图的坐标平面上有原点O与A、B、C、D四点.若有一直线L通过点(﹣3,4)且与y轴平行,则L也会通过的点为( )
A.点A B.点B C.点C D.点D
4.已知A、B两点的坐标分别是(﹣2,3)和(2,3),则下面四个结论:①点A在第四象限;②点B在第一象限;③线段AB平行于y轴;④点A、B之间的距离为4.其中正确的有( )
A.①③ B.②③ C.②④ D.②③④
5.过A(4,﹣2)和B(﹣2,﹣2)两点的直线一定( )
A.垂直于x轴 B.与y轴相交但不平于x轴
C.平行于x轴 D.与x轴、y轴平行
6.如图,右边坐标系中四边形的面积是( )
A.4 B.5.5 C.4.5 D.5
7.如图,在平面直角坐标系中,AB平行于x轴,点A坐标为(5,3),B在A点的左侧,AB=a,若B点在第二象限,则a的取值范围是( )
A.a>5 B.a≥5 C.a>3 D.a≥3
8.如图,直线l1⊥l2,在某平面直角坐标系中,x轴∥l2,y轴∥l1,点A的坐标为(2,3),点B的坐标为(﹣4,﹣1),则点C所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、填空题
9.已知AB∥y轴,点A的坐标为(3,2),且AB=3,则点B的坐标为 .
10.已知点A的坐标为(1,2),直线AB∥x轴,且AB=5,则点B坐标为 .
11.在y轴上,位于原点的下方,且距离原点3个单位长度的点的坐标是 .
12.定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若P(﹣1,1),Q(2,3),则P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.若点A(3,2),B(5,﹣3),M(6,m)满足点M分别到点A和点B的“实际距离”相等,则m= .
13.在平面直角坐标系xOy中,标出点A(﹣1,1),B(5,1)的位置,则线段AB的中点M的坐标是 .
14.矩形ABCD中,AB=5,BC=2,以矩形的左下角顶点A为原点,两边AB、AD为坐标轴建立直角坐标系,用坐标表示各顶点的坐标为 .
三、解答题
15.(1)在直角坐标系中,经过点A(﹣2,0)画平行于y轴的直线,这条直线上的点的坐标有什么特点?
(2)在直角坐标系中,经过点B(﹣2,﹣1)画平行于x轴的直线,这条直线上的点的坐标有什么特点?
16.在平面直角坐标系中将点(3,0),(3,2),(2,3),(2,5),(3,4),(4,5),(4,3),(3,2)用线段依次连接,可以得到一个图形,把这些点的横、纵坐标都乘﹣1,再将所得的各个点用线段依次连接起来,所得的图形与原图形相比有什么变化?
17.某邮递员投递区域街道如图所示,现在,他要把一封邮件从邮政局所在地点O处尽快送到A地.他选择的一条路径是(0,0)→(0,3)→(4,3)→(4,8)→(7,8).
(1)用彩笔在图中标出邮递员走的这条路径.
(2)用坐标写出由点O到点A的其他最短的路径.
18.如图,在直角坐标系中:
(1)写出A,B,C,D,E,F,O各点的坐标.
(2)在以上各点中,找出横坐标为0的点,这些点的位置有什么特点?
(3)在以上各点中,找出纵坐标为0的点,这些点的位置有什么特点?
(4)在以上各点中,纵坐标为3的点有哪几个?连接这几个点的直线与x轴有什么位置关系?
19.在如图所示的直角坐标系中,每个方格是边长为1的正方形,点A的坐标是(0,2).
(1)分别写出B,C,D三个点的坐标;
(2)将A,B,C,D四个点顺次连接起来,如果点E的坐标为(3,2),描出这个点,并说出点E是在四边形ABCD的内部,还是外部.
20.在直角坐标系中,有A(﹣2,3),B(2,﹣3),C(2,3),D(﹣2,﹣3),F(﹣3,4)五个点.
(1)哪个点与点F连接的线段与x轴、y轴都不相交?
(2)哪个点与点F连接的线段只与x轴相交,而不与y轴相交?
(3)哪个点与点F连接的线段与x轴和y轴都相交?
第1课时答案
一、单选题
C.C.D.C.B.D.D.B.
二、填空题
9.>;<.
10.4;(2,2),(﹣2,﹣2),(﹣2,2),(2,﹣2).
11.(﹣5,0).
12.(4,﹣4).
13.二、四、一.
14.四.
三、解答题
15.解:如图所示:
.
16.解:(1)∵点A在x轴上,
∴2a+8=0,
解得a=﹣4,
∴a﹣2=﹣6,
∴点A的坐标为(﹣6,0);
(2)∵点A在y轴上,
∴a﹣2=0,
解得a=2,
∴2a+8=12,
∴点A的坐标为(0,12).
17.解:A(0,3),B(1,1),C(4,0),D(1,﹣1),
E(0,﹣3),F(﹣1,﹣1),G(﹣4,0),H(﹣1,1).
18.解:根据题意,分两种情况讨论:
①1+2a=a﹣7,
解得:a=﹣8,
∴1+2a=a﹣7=﹣15,
∴点A的坐标为(﹣15,﹣15);
②1+2a+a﹣7=0,
解得:a=2,
∴1+2a=5,
a﹣7=﹣5,
∴点A的坐标为(5,﹣5),
综上所述:A点坐标为(﹣15,﹣15)或(5,﹣5).
19.解:(1)∵xy>0,
∴x、y同号,
∴点P(x,y)在第一、三象限;
(2)∵xy=0,
∴x、y至少有一个为0,
∴点P(x,y)在坐标轴上;
(3)∵xy<0,
∴x、y异号,
∴点P(x,y)在第二、四象限.
20.解:∵点M(3a﹣9,10﹣2a)在第二象限,且点M到x轴与y轴的距离相等,
∴(3a﹣9)+(10﹣2a)=0,
解得a=﹣1,
∴(a+2)2008﹣1=(﹣1+2)2008﹣1=1﹣1=0.
第2课时答案
一、单选题
B.B.A.C.C.C.A.B.
二、填空题
9.(3,﹣1)或(3,5).
10.(﹣4,2)或(6,2).
11.(0,﹣3).
12. 0.5.
13.(2,1).
14.A(0,0),B(5,0),C(5,2),D(0,2).
三、解答题
15.解:(1)经过点A(﹣2,0)画平行于y轴的直线,这条直线上的点的横坐标为2;
(2)经过点B(﹣2,﹣1)画平行于x轴的直线,这条直线上的点的纵坐标为﹣1.
16.解:如图,
所得的图形与原图形关于原点中心对称.
17.解:(1)如图所示,
(2)(0,0)→(4,0)→(4,3)→(4,8)→(7,8)表示一条点O到点A的最短的路径;
(0,0)→(4,0)→(7,0)→(7,8)表示一条点O到点A的最短的路径.
18.解:(1)A(2,3),B(﹣2,3),C(﹣4,﹣3),D(3,0),E(5,﹣4),F(0,3),O(0,0).
(2)横坐标为0的点为F(0,3),O(0,0),这些点都在y轴上.
(3)纵坐标为0的点为D(3,0),O(0,0),这些点都在x轴上.
(4)纵坐标为3的点为A(2,3),B(﹣2,3),F(0,3),连接这几个点的直线与x轴平行.
19.解:(1)B(1,﹣1),C(4,0),D(2,3);
(2)如图所示,点E在四边形ABCD的外部.
20.解:根据题意可得,A点在二象限,B点在第四象限,C点在第一象限,D点在第三象限,点F在第二象限.如图所示:
(1)点F与点A的连线不与x、y轴的相交;
(2)点F与点D的连线只与x轴相交,而不与y轴相交点;
(3)点F与点B的连线与x轴和y轴都相交.
第1课时
一、单选题
1.如图所示四个图形中,是平面直角坐标系的是( )
A. B.
C. D.
2.如图,两坐标轴x轴,y轴把平面直角坐标系分成四部分,则第(3)部分是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.下列说法中正确的是( )
A.点P(3,2)到x轴距离是3
B.在平面直角坐标系中,点(2,﹣3)和点(﹣2,3)表示同一个点
C.在平面直角坐标系中,第三象限内点的横坐标与纵坐标相等
D.若y=0,则点M(x,y)不属任何一个象限
4.已知点P的坐标为(2m﹣5,m﹣1),且点P到两坐标轴的距离相等,则点P的坐标为( )
A.(﹣1,﹣1) B.(3,3)或(1,﹣1)
C.(﹣1,1)或(3,3) D.(﹣3,﹣4)
5.如果点M(2a+4,a﹣1)在y轴上,那么点M的坐标是( )
A.(﹣2,﹣3) B.(0,﹣3) C.(﹣3,0) D.(0,1)
6.如果点P(a,b)在第三象限,那么点Q(﹣2a+3,b﹣1)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.如果点A既在x轴的上方,又在y轴的左边,且距离x轴,y轴分别为5个,4个单位,那么A点的坐标为( )
A.(5,﹣4) B.(4,﹣5) C.(﹣5,4) D.(﹣4,5)
8.下列与(﹣1,5)相连所得的直线与y轴平行的点为( )
A.(1,﹣5) B.(﹣1,2) C.(4,﹣5) D.(2,5)
二、填空题
9.如果点(a,﹣b)在第一象限,那么a 0,b 0(填“>”或“<”).
10.到x轴和y轴的距离都等于2的点有 个,坐标分别为 .
11.如果点P(m﹣3,2+m)在x轴上,那么点P的坐标是 .
12.在平面直角坐标系中,点A的坐标为(a﹣1,a+1),B的坐标为(a+3,a﹣5),若点A在y轴上,则点B的坐标为 .
13.已知点P(a,b)在第三象限,那么点Q(a,﹣b)在第 象限,点M(﹣a,b)在第 象限,点N(﹣a,﹣b)在第 象限.
14.已知A(x+2,2y﹣3)在第二象限,则B(1﹣x,5﹣4y)在第 象限.
三、解答题
15.先画出直角坐标系,再描出下列各点:
A(5,3),B(﹣2,6),C(2,﹣3),D(﹣4,﹣3),E(﹣3,0),F(0,4).
16.在平面直角坐标系中,点A(a﹣2,2a+8),根据下列条件分别求a以及点A的坐标:
(1)当点A在x轴上;
(2)当点A在y轴上.
17.如图,A,B,C,D,E,F,G,H分别是直角坐标系中的点,分别写出各点的坐标.
18.已知点A(1+2a,a﹣7)到两坐标轴的距离相等,求A点坐标.
19.已知点P(x,y).
(1)当xy>0时,点P(x,y)在第几象限?
(2)当xy=0时,点P(x,y)在什么位置?
(3)当xy<0时,点P(x,y)在第几象限?
20.若点M(3a﹣9,10﹣2a)在第二象限,且点M到x轴与y轴的距离相等,试求(a+2)2008﹣1的值.
第2课时
一、单选题
1.过点A(﹣3,2)和B(﹣3,5)作直线,则直线AB( )
A.与x轴平行 B.与y轴平行
C.与y轴相交 D.与x轴,y轴均相交
2.下列语句正确的是( )
A.平行于x轴的直线上所有点的横坐标都相同
B.(﹣3,5)与(5,﹣3)表示两个不同的点
C.若点P(a,b)在y轴上,则b=0
3.如图的坐标平面上有原点O与A、B、C、D四点.若有一直线L通过点(﹣3,4)且与y轴平行,则L也会通过的点为( )
A.点A B.点B C.点C D.点D
4.已知A、B两点的坐标分别是(﹣2,3)和(2,3),则下面四个结论:①点A在第四象限;②点B在第一象限;③线段AB平行于y轴;④点A、B之间的距离为4.其中正确的有( )
A.①③ B.②③ C.②④ D.②③④
5.过A(4,﹣2)和B(﹣2,﹣2)两点的直线一定( )
A.垂直于x轴 B.与y轴相交但不平于x轴
C.平行于x轴 D.与x轴、y轴平行
6.如图,右边坐标系中四边形的面积是( )
A.4 B.5.5 C.4.5 D.5
7.如图,在平面直角坐标系中,AB平行于x轴,点A坐标为(5,3),B在A点的左侧,AB=a,若B点在第二象限,则a的取值范围是( )
A.a>5 B.a≥5 C.a>3 D.a≥3
8.如图,直线l1⊥l2,在某平面直角坐标系中,x轴∥l2,y轴∥l1,点A的坐标为(2,3),点B的坐标为(﹣4,﹣1),则点C所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、填空题
9.已知AB∥y轴,点A的坐标为(3,2),且AB=3,则点B的坐标为 .
10.已知点A的坐标为(1,2),直线AB∥x轴,且AB=5,则点B坐标为 .
11.在y轴上,位于原点的下方,且距离原点3个单位长度的点的坐标是 .
12.定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若P(﹣1,1),Q(2,3),则P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.若点A(3,2),B(5,﹣3),M(6,m)满足点M分别到点A和点B的“实际距离”相等,则m= .
13.在平面直角坐标系xOy中,标出点A(﹣1,1),B(5,1)的位置,则线段AB的中点M的坐标是 .
14.矩形ABCD中,AB=5,BC=2,以矩形的左下角顶点A为原点,两边AB、AD为坐标轴建立直角坐标系,用坐标表示各顶点的坐标为 .
三、解答题
15.(1)在直角坐标系中,经过点A(﹣2,0)画平行于y轴的直线,这条直线上的点的坐标有什么特点?
(2)在直角坐标系中,经过点B(﹣2,﹣1)画平行于x轴的直线,这条直线上的点的坐标有什么特点?
16.在平面直角坐标系中将点(3,0),(3,2),(2,3),(2,5),(3,4),(4,5),(4,3),(3,2)用线段依次连接,可以得到一个图形,把这些点的横、纵坐标都乘﹣1,再将所得的各个点用线段依次连接起来,所得的图形与原图形相比有什么变化?
17.某邮递员投递区域街道如图所示,现在,他要把一封邮件从邮政局所在地点O处尽快送到A地.他选择的一条路径是(0,0)→(0,3)→(4,3)→(4,8)→(7,8).
(1)用彩笔在图中标出邮递员走的这条路径.
(2)用坐标写出由点O到点A的其他最短的路径.
18.如图,在直角坐标系中:
(1)写出A,B,C,D,E,F,O各点的坐标.
(2)在以上各点中,找出横坐标为0的点,这些点的位置有什么特点?
(3)在以上各点中,找出纵坐标为0的点,这些点的位置有什么特点?
(4)在以上各点中,纵坐标为3的点有哪几个?连接这几个点的直线与x轴有什么位置关系?
19.在如图所示的直角坐标系中,每个方格是边长为1的正方形,点A的坐标是(0,2).
(1)分别写出B,C,D三个点的坐标;
(2)将A,B,C,D四个点顺次连接起来,如果点E的坐标为(3,2),描出这个点,并说出点E是在四边形ABCD的内部,还是外部.
20.在直角坐标系中,有A(﹣2,3),B(2,﹣3),C(2,3),D(﹣2,﹣3),F(﹣3,4)五个点.
(1)哪个点与点F连接的线段与x轴、y轴都不相交?
(2)哪个点与点F连接的线段只与x轴相交,而不与y轴相交?
(3)哪个点与点F连接的线段与x轴和y轴都相交?
第1课时答案
一、单选题
C.C.D.C.B.D.D.B.
二、填空题
9.>;<.
10.4;(2,2),(﹣2,﹣2),(﹣2,2),(2,﹣2).
11.(﹣5,0).
12.(4,﹣4).
13.二、四、一.
14.四.
三、解答题
15.解:如图所示:
.
16.解:(1)∵点A在x轴上,
∴2a+8=0,
解得a=﹣4,
∴a﹣2=﹣6,
∴点A的坐标为(﹣6,0);
(2)∵点A在y轴上,
∴a﹣2=0,
解得a=2,
∴2a+8=12,
∴点A的坐标为(0,12).
17.解:A(0,3),B(1,1),C(4,0),D(1,﹣1),
E(0,﹣3),F(﹣1,﹣1),G(﹣4,0),H(﹣1,1).
18.解:根据题意,分两种情况讨论:
①1+2a=a﹣7,
解得:a=﹣8,
∴1+2a=a﹣7=﹣15,
∴点A的坐标为(﹣15,﹣15);
②1+2a+a﹣7=0,
解得:a=2,
∴1+2a=5,
a﹣7=﹣5,
∴点A的坐标为(5,﹣5),
综上所述:A点坐标为(﹣15,﹣15)或(5,﹣5).
19.解:(1)∵xy>0,
∴x、y同号,
∴点P(x,y)在第一、三象限;
(2)∵xy=0,
∴x、y至少有一个为0,
∴点P(x,y)在坐标轴上;
(3)∵xy<0,
∴x、y异号,
∴点P(x,y)在第二、四象限.
20.解:∵点M(3a﹣9,10﹣2a)在第二象限,且点M到x轴与y轴的距离相等,
∴(3a﹣9)+(10﹣2a)=0,
解得a=﹣1,
∴(a+2)2008﹣1=(﹣1+2)2008﹣1=1﹣1=0.
第2课时答案
一、单选题
B.B.A.C.C.C.A.B.
二、填空题
9.(3,﹣1)或(3,5).
10.(﹣4,2)或(6,2).
11.(0,﹣3).
12. 0.5.
13.(2,1).
14.A(0,0),B(5,0),C(5,2),D(0,2).
三、解答题
15.解:(1)经过点A(﹣2,0)画平行于y轴的直线,这条直线上的点的横坐标为2;
(2)经过点B(﹣2,﹣1)画平行于x轴的直线,这条直线上的点的纵坐标为﹣1.
16.解:如图,
所得的图形与原图形关于原点中心对称.
17.解:(1)如图所示,
(2)(0,0)→(4,0)→(4,3)→(4,8)→(7,8)表示一条点O到点A的最短的路径;
(0,0)→(4,0)→(7,0)→(7,8)表示一条点O到点A的最短的路径.
18.解:(1)A(2,3),B(﹣2,3),C(﹣4,﹣3),D(3,0),E(5,﹣4),F(0,3),O(0,0).
(2)横坐标为0的点为F(0,3),O(0,0),这些点都在y轴上.
(3)纵坐标为0的点为D(3,0),O(0,0),这些点都在x轴上.
(4)纵坐标为3的点为A(2,3),B(﹣2,3),F(0,3),连接这几个点的直线与x轴平行.
19.解:(1)B(1,﹣1),C(4,0),D(2,3);
(2)如图所示,点E在四边形ABCD的外部.
20.解:根据题意可得,A点在二象限,B点在第四象限,C点在第一象限,D点在第三象限,点F在第二象限.如图所示:
(1)点F与点A的连线不与x、y轴的相交;
(2)点F与点D的连线只与x轴相交,而不与y轴相交点;
(3)点F与点B的连线与x轴和y轴都相交.
