内蒙古包头市铁路第一中学2022-2023学年高二下学期期末考试数学(文)试题(含答案)
文档属性
| 名称 | 内蒙古包头市铁路第一中学2022-2023学年高二下学期期末考试数学(文)试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 435.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-01 00:00:00 | ||
图片预览



文档简介
包头市铁路第一中学2022-2023学年高二下学期期末考试
文科数学
一、单选题(本大题共12小题,共60.0分.在每小题列出的选项中,选出符合题目的一项)
1.若集合,则( )
A. B. C. D.
2.设函数,则下列函数中为奇函数的是( )
A. B. C. D.
3.若则( )
A. B. C. D.
4.函数的零点所在的区间为( )
A. B. C. D.
5.设O为平面坐标系的坐标原点,在区域内随机取一点,记该点为A,则直线的倾斜角不大于的概率为( )
A. B. C. D.
6.甲、乙两名同学在高考前的5次模拟考中的数学成绩如茎叶图所示,记甲、乙两人的平均成绩分别为x,y,下列说法正确的是( )
A.,且乙比甲的成绩稳定 B.,且乙比甲的成绩稳定
C.,且甲比乙的成绩稳定 D.,且甲比乙的成绩稳定
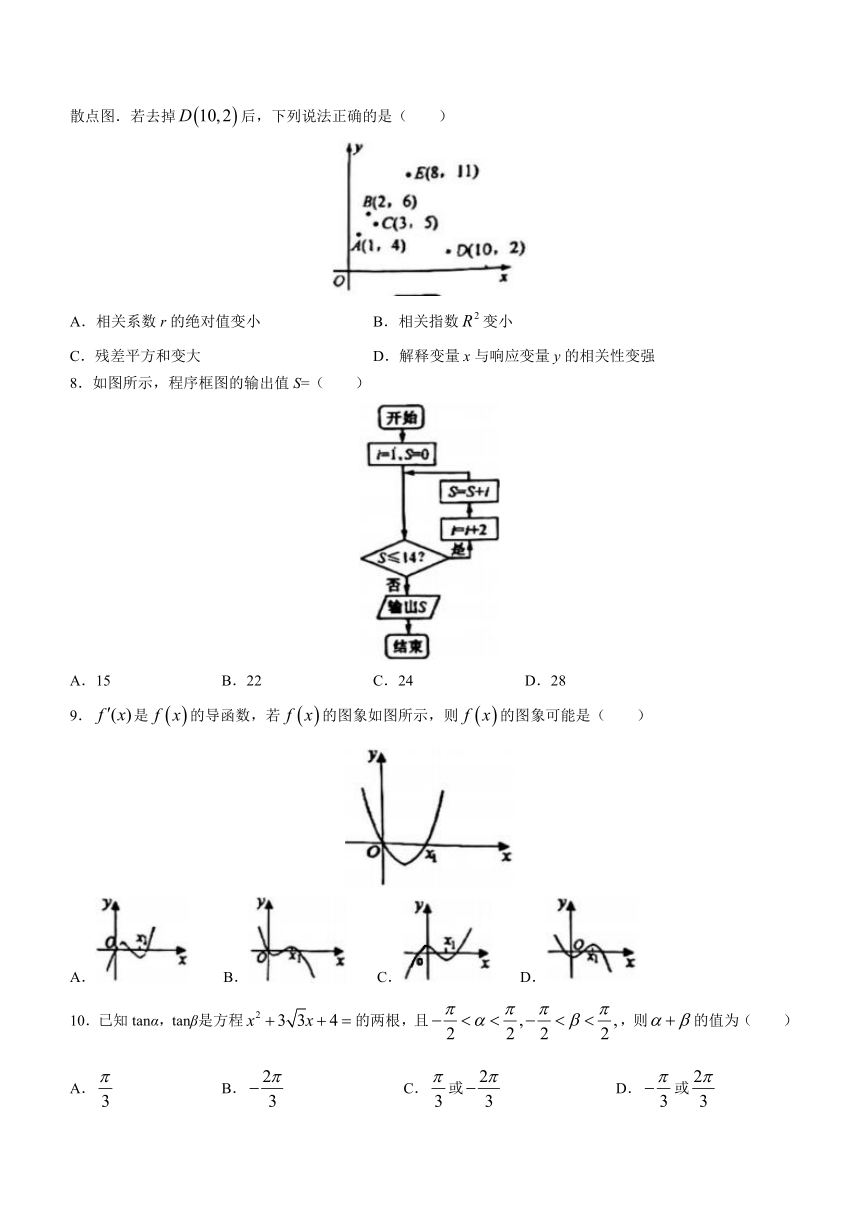
7.某兴趣小组研究光照时长和向日葵种子发芽数量y(颗)之间的关系,采集5组数据,作如图所示的散点图.若去掉后,下列说法正确的是( )
A.相关系数r的绝对值变小 B.相关指数变小
C.残差平方和变大 D.解释变量x与响应变量y的相关性变强
8.如图所示,程序框图的输出值S=( )
A.15 B.22 C.24 D.28
9.是的导函数,若的图象如图所示,则的图象可能是( )
A. B. C. D.
10.已知tanα,tanβ是方程的两根,且,则的值为( )
A. B. C.或 D.或
11.函数)的部分图象如图所示,则,的值为( )
A.2, B.1, C.1, D.2,
12.已知函数,则下面结论中不正确的是( )
A.最小正周期为π B.函数关于对称
C.函数在区间有最大值为 D.函数在区间单调递增
二、填空题(本大题共4小题,共20.0分)
13.某高三年级一共有800人,要从中随机抽取50人参加社团比赛,按系统抽样的方法进行等距抽取,将金体学生进行编号分别为1~800,并按编号分成50组,若第3组抽取的编号为36,则第16组抽取的编号为_________.
14.若是上的增函数,则a的取值范围是_________.
15.若曲线在处的切线经过点,则实数a=_________.
16.若图的半径是2cm,则30°的圆心角与圆弧所围成的扇形的面积是_________
三、解答题(本大题共6小题,共70.0分.解答应写出文字说明,证明过程或演算步骤)
17.已知幂函数为偶函数.
(1)求的解析式;
(2)若在上不是单调函数,求实数a的取值范围.
18.已知集合.
(1)若和的充分不必要条件,求实数a的取值范围;
(2)设命题,若命题p为假命题,求实数m的取值范围.
19.已知函数.
(1)求函数的最小正周期;
(2)将函数的图象先向左平移一个单位,然后纵坐标不变,横坐标缩短为原来的倍,得到函数的图象,当时,求函数的值域.
20.某学校为了调查该校学生在一周零食方面的支出情况,抽出了一个容量为n的样本,分成四组,,,,其频率分布直方图如图所示,其中支出在元的学生有180人.
(1)请求出n的值;
(2)请以样本估计全校学生的平均支出为多少元(同一组的数据用该区间的中点值作代表);
(3)如果采用分层抽样的方法从,共抽取5人,然后从中选取2人参加学校进一步的座谈会求在[30,40).[40,50)中正好各抽取一人的概率为多少.
21.为推动实施健康中国战略,树立国家大卫生、大健康观念,手机也推出了多款健康运动软件,如“微信运动”,某运动品牌公司140名员工均在微信好友群中参与了“微信运动”,且公司每月进行一次评比,对该月内每日运动都达到10000步及以上的员工授予该月“运动达人”称号,其余员工均称为“参与者”,下表是该运动品牌公司140名员工2021年1月-5月获得“运动达人”称号的统计数据:
月份 1 2 3 4 5
“运动达人”员工数 120 105 100 95 80
(1)由表中看出,可用线性回归模型拟合“运动达人”员工数y与月份x之间的关系,求,关于x的回归直线方程,并预测该运动品牌公司6月份获得“运动达人”称号的员工数;
(2)为了进一步了解员工们的运动情况,选取了员工们在3月份的运动数据进行分析,统计结果如下:
运动达人 参与者 合计
男员工 60 80
女员工 n 20 60
合计 100 40 140
请补充上表中的数据(直接写出m,n的值).并根据上表判断是否有95%的把握认为获得“运动达人”称号与性别有关
参考公式:
0.10 0.05 0.025 0.001
2.706 3.841 5.024 6.635
22.(本小题12.0分)
已知函数,
(1)讨论的单调性;
(2)求曲线过坐标原点的切线与曲线的公共点的坐标.
包头市铁路第一中学2022-2023学年高二下学期期末考试
文科期末试题答案
1.B 2.B 3.A 4.C 5.C 6.A 7.D
8.A 9.C 10.B 11.D 12.D
13.244 14. 15. 16.
17.解:(1)由题意,为幂函数,
所以,解得:或,
因为是偶函数,则,
所以;
(2),
若在上不是单调函数,
则,解得:,
故实数a的取值范围是.
18.解:(1)∵,
,
因为是的充分不必要条件,所以
所以,解得,
故a的取值范围为.
(2)命题p:.的否定为
:,.
∵命题p为假命题,
∴命题为真命题,
即恒成立.
令,
则,
即,
解得.
∴实数m的取值范围是.
19.解:(1)
,
所以函数的最小正周期为;
(2)将函数的图象先向左平移个单位,得,
然后纵坐标不变,横坐标缩短为原来的倍,得,
由,则,所以,
所以.
20.解:(1)由于支出在的人的频率为,
所以(人).
(2)该校学生的平均支出为元.
(3)采用分层抽样抽取的[30,40),[40,50)的人数比应为.
所以5人中有2人零食支出在[30,40),记为a,b:
有3人零食支出在[40,50),记为A,B,C.
从这5人中选取2人有ab,aA,aB,aC,bA,bB,bC,AB,AC,BC,共10种情况
其中[30,40),[40,50)中正好各抽取一人有aA,aB,aC,bA,bB,bC,共6种情况,
所以在[30,40),[40,50)中正好各抽取一人的概率为.
21.解:(1)由表格数据得:,.
所以,,
所以y关于x的回归直线方程为.
令,则.
即预测该运动品牌分公司6月份获得“运动达人”称号的员工数为73;
(2)依题意,..
根据列联表数据得:.
所以没有95%的把握认为获得“运动达人”称号与性别有关.
22.解:(1)
①当,由时,由于的图象是开口向上的抛物线,故此时,则在R上单调递增:
②当,图时,令,解得.
令,解得或,令,解得,
∴在,单调递增,在单调递减;
综上,当时,在R上单调递增;
当时,在单调递增,在单调递减.
(2)设曲线过坐标原点的切线为l,切点为,,
则切线方程为,
将原点代入切线方程有,,解得.
∴切线方程为,
令,,解得或,
∴曲线过坐标原点的切线与曲线的公共点的坐标为和.
文科数学
一、单选题(本大题共12小题,共60.0分.在每小题列出的选项中,选出符合题目的一项)
1.若集合,则( )
A. B. C. D.
2.设函数,则下列函数中为奇函数的是( )
A. B. C. D.
3.若则( )
A. B. C. D.
4.函数的零点所在的区间为( )
A. B. C. D.
5.设O为平面坐标系的坐标原点,在区域内随机取一点,记该点为A,则直线的倾斜角不大于的概率为( )
A. B. C. D.
6.甲、乙两名同学在高考前的5次模拟考中的数学成绩如茎叶图所示,记甲、乙两人的平均成绩分别为x,y,下列说法正确的是( )
A.,且乙比甲的成绩稳定 B.,且乙比甲的成绩稳定
C.,且甲比乙的成绩稳定 D.,且甲比乙的成绩稳定
7.某兴趣小组研究光照时长和向日葵种子发芽数量y(颗)之间的关系,采集5组数据,作如图所示的散点图.若去掉后,下列说法正确的是( )
A.相关系数r的绝对值变小 B.相关指数变小
C.残差平方和变大 D.解释变量x与响应变量y的相关性变强
8.如图所示,程序框图的输出值S=( )
A.15 B.22 C.24 D.28
9.是的导函数,若的图象如图所示,则的图象可能是( )
A. B. C. D.
10.已知tanα,tanβ是方程的两根,且,则的值为( )
A. B. C.或 D.或
11.函数)的部分图象如图所示,则,的值为( )
A.2, B.1, C.1, D.2,
12.已知函数,则下面结论中不正确的是( )
A.最小正周期为π B.函数关于对称
C.函数在区间有最大值为 D.函数在区间单调递增
二、填空题(本大题共4小题,共20.0分)
13.某高三年级一共有800人,要从中随机抽取50人参加社团比赛,按系统抽样的方法进行等距抽取,将金体学生进行编号分别为1~800,并按编号分成50组,若第3组抽取的编号为36,则第16组抽取的编号为_________.
14.若是上的增函数,则a的取值范围是_________.
15.若曲线在处的切线经过点,则实数a=_________.
16.若图的半径是2cm,则30°的圆心角与圆弧所围成的扇形的面积是_________
三、解答题(本大题共6小题,共70.0分.解答应写出文字说明,证明过程或演算步骤)
17.已知幂函数为偶函数.
(1)求的解析式;
(2)若在上不是单调函数,求实数a的取值范围.
18.已知集合.
(1)若和的充分不必要条件,求实数a的取值范围;
(2)设命题,若命题p为假命题,求实数m的取值范围.
19.已知函数.
(1)求函数的最小正周期;
(2)将函数的图象先向左平移一个单位,然后纵坐标不变,横坐标缩短为原来的倍,得到函数的图象,当时,求函数的值域.
20.某学校为了调查该校学生在一周零食方面的支出情况,抽出了一个容量为n的样本,分成四组,,,,其频率分布直方图如图所示,其中支出在元的学生有180人.
(1)请求出n的值;
(2)请以样本估计全校学生的平均支出为多少元(同一组的数据用该区间的中点值作代表);
(3)如果采用分层抽样的方法从,共抽取5人,然后从中选取2人参加学校进一步的座谈会求在[30,40).[40,50)中正好各抽取一人的概率为多少.
21.为推动实施健康中国战略,树立国家大卫生、大健康观念,手机也推出了多款健康运动软件,如“微信运动”,某运动品牌公司140名员工均在微信好友群中参与了“微信运动”,且公司每月进行一次评比,对该月内每日运动都达到10000步及以上的员工授予该月“运动达人”称号,其余员工均称为“参与者”,下表是该运动品牌公司140名员工2021年1月-5月获得“运动达人”称号的统计数据:
月份 1 2 3 4 5
“运动达人”员工数 120 105 100 95 80
(1)由表中看出,可用线性回归模型拟合“运动达人”员工数y与月份x之间的关系,求,关于x的回归直线方程,并预测该运动品牌公司6月份获得“运动达人”称号的员工数;
(2)为了进一步了解员工们的运动情况,选取了员工们在3月份的运动数据进行分析,统计结果如下:
运动达人 参与者 合计
男员工 60 80
女员工 n 20 60
合计 100 40 140
请补充上表中的数据(直接写出m,n的值).并根据上表判断是否有95%的把握认为获得“运动达人”称号与性别有关
参考公式:
0.10 0.05 0.025 0.001
2.706 3.841 5.024 6.635
22.(本小题12.0分)
已知函数,
(1)讨论的单调性;
(2)求曲线过坐标原点的切线与曲线的公共点的坐标.
包头市铁路第一中学2022-2023学年高二下学期期末考试
文科期末试题答案
1.B 2.B 3.A 4.C 5.C 6.A 7.D
8.A 9.C 10.B 11.D 12.D
13.244 14. 15. 16.
17.解:(1)由题意,为幂函数,
所以,解得:或,
因为是偶函数,则,
所以;
(2),
若在上不是单调函数,
则,解得:,
故实数a的取值范围是.
18.解:(1)∵,
,
因为是的充分不必要条件,所以
所以,解得,
故a的取值范围为.
(2)命题p:.的否定为
:,.
∵命题p为假命题,
∴命题为真命题,
即恒成立.
令,
则,
即,
解得.
∴实数m的取值范围是.
19.解:(1)
,
所以函数的最小正周期为;
(2)将函数的图象先向左平移个单位,得,
然后纵坐标不变,横坐标缩短为原来的倍,得,
由,则,所以,
所以.
20.解:(1)由于支出在的人的频率为,
所以(人).
(2)该校学生的平均支出为元.
(3)采用分层抽样抽取的[30,40),[40,50)的人数比应为.
所以5人中有2人零食支出在[30,40),记为a,b:
有3人零食支出在[40,50),记为A,B,C.
从这5人中选取2人有ab,aA,aB,aC,bA,bB,bC,AB,AC,BC,共10种情况
其中[30,40),[40,50)中正好各抽取一人有aA,aB,aC,bA,bB,bC,共6种情况,
所以在[30,40),[40,50)中正好各抽取一人的概率为.
21.解:(1)由表格数据得:,.
所以,,
所以y关于x的回归直线方程为.
令,则.
即预测该运动品牌分公司6月份获得“运动达人”称号的员工数为73;
(2)依题意,..
根据列联表数据得:.
所以没有95%的把握认为获得“运动达人”称号与性别有关.
22.解:(1)
①当,由时,由于的图象是开口向上的抛物线,故此时,则在R上单调递增:
②当,图时,令,解得.
令,解得或,令,解得,
∴在,单调递增,在单调递减;
综上,当时,在R上单调递增;
当时,在单调递增,在单调递减.
(2)设曲线过坐标原点的切线为l,切点为,,
则切线方程为,
将原点代入切线方程有,,解得.
∴切线方程为,
令,,解得或,
∴曲线过坐标原点的切线与曲线的公共点的坐标为和.
同课章节目录
