2023-2024学年沪科版七年级数学上册3.2 一元一次方程的应用 第4课时(比例分配问题)课件 20张PPT
文档属性
| 名称 | 2023-2024学年沪科版七年级数学上册3.2 一元一次方程的应用 第4课时(比例分配问题)课件 20张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-31 13:31:55 | ||
图片预览






文档简介
(共20张PPT)
第4课时 分配问题
第3章 一次方程与方程组
3.2 一元一次方程的应用
沪科版数学七年级上册
【知识与技能】
1.使学生学会列一元一次方程解有关和、差、倍、分问题的应用题.
2.通过应用题教学使学生进一步使用代数中的方程去反映现实中的相等关系,体会方程方法的优越性.
【过程与方法】
1.根据具体问题的数量关系,形成方程的模型,进一步培养学生利用方程的观点认识现实世界的意识和能力.
2.通过分组合作学习活动,学会在活动中与人合作,并能与他人交流思维的过程与结果.
【情感、态度与价值观】
通过由具体实例的分析、思考与合作学习的过程,感受数学的应用价值,提高分析问题、解决问题的能力
学习目标
知识回顾
列一元一次方程解决实际问题的一般步骤:
审题
找等量关系
设未知数
列方程
解方程
检验
作答
关键
解要符合实际意义
可以列方程: .
新知导入
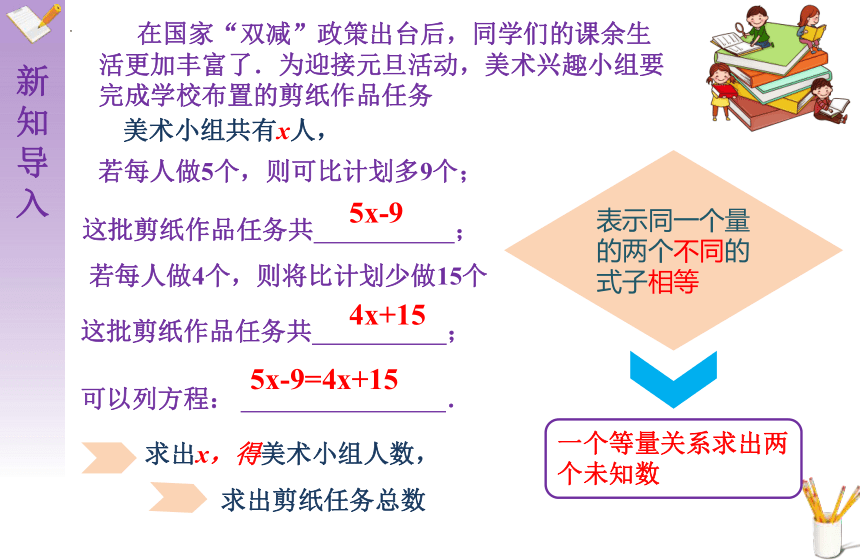
在国家“双减”政策出台后,同学们的课余生活更加丰富了.为迎接元旦活动,美术兴趣小组要完成学校布置的剪纸作品任务
若每人做5个,则可比计划多9个;
若每人做4个,则将比计划少做15个
美术小组共有x人,
这批剪纸作品任务共 ;
这批剪纸作品任务共 ;
表示同一个量的两个不同的式子相等
5x-9
4x+15
5x-9=4x+15
求出x,得美术小组人数,
求出剪纸任务总数
一个等量关系求出两个未知数
在国家“双减”政策出台后,同学们的课余生活更加丰富了.为迎接元旦活动,美术兴趣小组要完成学校布置的剪纸作品任务,若每人做5个,则可比计划多9个;若每人做4个,则将比计划少做15个,求这批剪纸作品任务共多少个?
请同学们列出方程解应用题
解:设美术小组共有x人,由题意得
5x-9=4x+15
解方程得 x=24
5x-9=5×24-9=111(件)
答:这批剪纸作品任务共111个
新知讲解
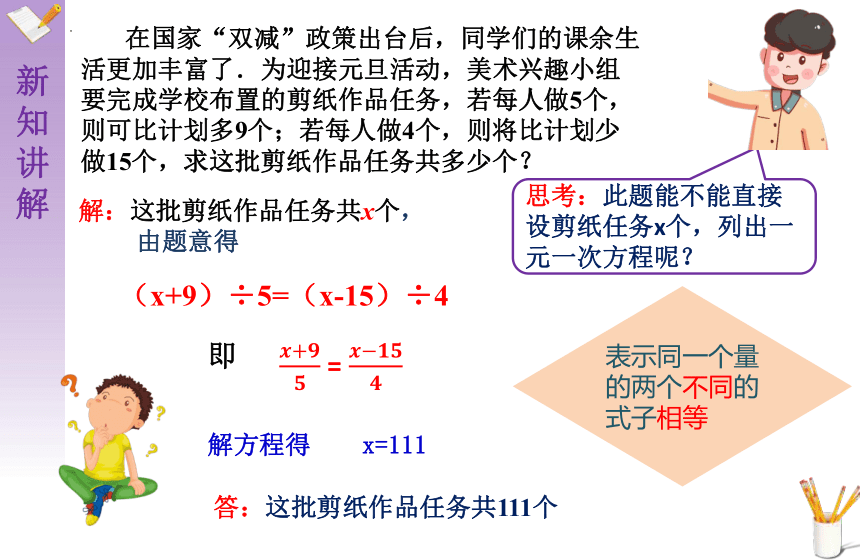
在国家“双减”政策出台后,同学们的课余生活更加丰富了.为迎接元旦活动,美术兴趣小组要完成学校布置的剪纸作品任务,若每人做5个,则可比计划多9个;若每人做4个,则将比计划少做15个,求这批剪纸作品任务共多少个?
思考:此题能不能直接设剪纸任务x个,列出一元一次方程呢?
解:这批剪纸作品任务共x个,
由题意得
(x+9)÷5=(x-15)÷4
表示同一个量的两个不同的式子相等
=
即
解方程得 x=111
答:这批剪纸作品任务共111个
新知讲解
新知讲解
例1、 在学校开展“劳动创造美好生活”主题系列活动中,七年级(1)班负责校园某绿化角的设计、种植与养护.
同学们计划将预算经费390元全部用于购买绿萝和吊兰两种绿植,根据设计3盆绿萝数配2盆吊兰。已知绿萝每盆9元,吊兰每盆6元,问可购买绿萝和吊兰各多少盆?
分析:
3盆绿萝配2盆吊兰
绿萝盆数 :吊兰盆数=3 :2
预算经费390元全部用于购买绿萝和吊兰
绿萝费用+吊兰费用 = 390
解:可购买绿萝3x盆,吊兰盆数2x盆,由题意可得
9×3x+6×2x=390
解方程得 x=10
3x=30(盆)
2x=30(盆)
答:可买绿萝30盆,吊兰20盆
分配问题是较复杂的应用题之一
常见的两种基本相等关系:
(1) 总量=各部分量的和;
(2) 表示同一个量的两个不同的式子相等.
设问题中的多个未知量的其中一个为x,利用与未知量密切相关的一个等量关系式表示出另一个未知量,最后利用另外一个等量关系列出方程。
新知总结
成人票数+学生票数=1000张 ①
成人票款+学生票款=6950元 ②
例2、某文艺团为“希望工程”募捐组织了一场义演,共售出1 000张票,筹得票款6 950元.成人票与学生票各售出多少张?
讨论:上面的问题中包含哪些等量关系?
例题精讲
设售出的学生票为x张,填写下表:
学生 成人
票数/张
票款/元
x
1000-x
5x
8(1000-x)
根据等量关系②,列出方程并求解
例2、某文艺团为“希望工程”募捐组织了一场义演,共售出1 000张票,筹得票款6 950元.成人票与学生票各售出多少张?
解:设售出的学生票为x张,由题意得:
5x+8(1000-x)=6950
解这个方程,得x=350.
1000-x=1000-350=650(张)
答:售出成人票650张,学生票350张.
例2、某文艺团为“希望工程”募捐组织了一场义演,共售出1 000张票,筹得票款6 950元.成人票与学生票各售出多少张?
讨论:设所得的学生票款为y元,填写下表:
学生 成人
票数/张
票款/元
6950-y
y
根据等量关系①
,列出方程并求解
解:设所得的学生票款为y元,由题意得:
解这个方程,
得 y=1750.
(张)
(张)
答:售出成人票650张,学生票350张.
想 一 想
因为票的数量为整数张,所以所得票款不可能是6930元.
如果票价不变,售出1000张票后所得票款可能是 6930 元吗? 为什么?
解:设售出学生票x张,由题意得
例2、某文艺团为“希望工程”募捐组织了一场义演,共售出1 000张票,筹得票款6 950元.成人票与学生票各售出多少张?
1、兄弟两人合伙从事经营,哥哥入股25000元,弟弟入股20000元,一年后盈利8352元.按入股的资金比例分配,兄弟两人各应分得盈利多少元?
解方程得
x=4640
8352-x=3712
答:哥哥应分得盈利4640元,
弟弟应分得盈利3712元.
课堂练习
解:设哥哥分得盈利x元,弟弟分得剩下的盈利(8352-x)元.由题意得
x:(8352-x)=25000:20000
2、 某县矿山机械设备闻名省内外.在某矿山机械设备车间工人正在紧张地按订单进度进行生产,若每人每天平均可以生产轴承12个或者轴杆16个,1个轴承与2个轴杆组成一套,该车间共有90人,应该怎样调配人力,才能使每天生产的轴承和轴杆正好配套?
轴杆总数=轴承总数的2倍
等量关系
解:设生产轴承有x人,生产轴杆(90-x)人,由题意可得
16(90-x) =2×12x
x=36
90-x=54(人)
1个轴承与2个轴杆组成一套
答:生产轴承有36人,生产轴杆54人,正好配套
课堂练习
3.某商店今年共销售21英寸(54cm)、25英寸(64cm)、29英寸(74cm)3种彩电360台,它们的销售数量的比是1:7:4,这3种彩各销售了多少台?
课堂练习
分析:这个问题中数量之间的相等关系是:
21英寸的销售数量+25英寸的销售数量+29英寸的销售数量=360
解:设21英寸的彩电销售了x台.
根据题意,得x+7x+4x=360.
解这个方程,得x=30.
答:这3种彩电各销售了30、210、120台.
拓展延伸
1、我国古代数学著作《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽,问:城中家几何?
大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完,问:城中有多少户人家?在这个问题中,城中人家的户数为( )
A.25 B. 75 C.81 D.90
B
提示:
城中人家的户数=剩下的鹿的3倍
2、 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”
诗中后面两句的意思是:如果一间客房住7人,那么有7人无房可住;如果一间客房住9人,那么就空出一间客房,若设该店有客房x间,可列出关于x的一元一次方程 。
拓展延伸
7x+7=9(x-1)
提示:
客人总数一个量两种表达
课堂小结
列方程解应用题的步骤:
(1)审题,找等量关系
(2)设未知数
(3)列方程
(4)解方程
(5)写出答案
在和、差、倍、分问题中,
量与量之间都存在着关系式:
表示同一个量的两个不同的式子相等
各分量之和=总量.
1、《九章算术》是我国古代的数学专著,几名学生要凑钱购买1本.若每人出8元,则多了3元;若每人出7元,则少了4元.问学生人数和该书单价各是多少?
补充练习
2、某班学生分两组参加植树活动,甲组有17人,乙组有25人,后来由于需要,从甲组抽调了部分学生去乙组,结果乙组的人数是甲组的2倍,从甲组抽调了多少学生去乙组?
补充练习
3、明代数学家程大位所著的《算法统宗》中有这样一个问题:“隔墙听得客分银,不知人数不知银.七两分之多四两,九两分之少半斤.”其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两.请问:所分的银子共有 两. (注:明代时1斤=16两,故有“半斤八两”这个成语)
46
第4课时 分配问题
第3章 一次方程与方程组
3.2 一元一次方程的应用
沪科版数学七年级上册
【知识与技能】
1.使学生学会列一元一次方程解有关和、差、倍、分问题的应用题.
2.通过应用题教学使学生进一步使用代数中的方程去反映现实中的相等关系,体会方程方法的优越性.
【过程与方法】
1.根据具体问题的数量关系,形成方程的模型,进一步培养学生利用方程的观点认识现实世界的意识和能力.
2.通过分组合作学习活动,学会在活动中与人合作,并能与他人交流思维的过程与结果.
【情感、态度与价值观】
通过由具体实例的分析、思考与合作学习的过程,感受数学的应用价值,提高分析问题、解决问题的能力
学习目标
知识回顾
列一元一次方程解决实际问题的一般步骤:
审题
找等量关系
设未知数
列方程
解方程
检验
作答
关键
解要符合实际意义
可以列方程: .
新知导入
在国家“双减”政策出台后,同学们的课余生活更加丰富了.为迎接元旦活动,美术兴趣小组要完成学校布置的剪纸作品任务
若每人做5个,则可比计划多9个;
若每人做4个,则将比计划少做15个
美术小组共有x人,
这批剪纸作品任务共 ;
这批剪纸作品任务共 ;
表示同一个量的两个不同的式子相等
5x-9
4x+15
5x-9=4x+15
求出x,得美术小组人数,
求出剪纸任务总数
一个等量关系求出两个未知数
在国家“双减”政策出台后,同学们的课余生活更加丰富了.为迎接元旦活动,美术兴趣小组要完成学校布置的剪纸作品任务,若每人做5个,则可比计划多9个;若每人做4个,则将比计划少做15个,求这批剪纸作品任务共多少个?
请同学们列出方程解应用题
解:设美术小组共有x人,由题意得
5x-9=4x+15
解方程得 x=24
5x-9=5×24-9=111(件)
答:这批剪纸作品任务共111个
新知讲解
在国家“双减”政策出台后,同学们的课余生活更加丰富了.为迎接元旦活动,美术兴趣小组要完成学校布置的剪纸作品任务,若每人做5个,则可比计划多9个;若每人做4个,则将比计划少做15个,求这批剪纸作品任务共多少个?
思考:此题能不能直接设剪纸任务x个,列出一元一次方程呢?
解:这批剪纸作品任务共x个,
由题意得
(x+9)÷5=(x-15)÷4
表示同一个量的两个不同的式子相等
=
即
解方程得 x=111
答:这批剪纸作品任务共111个
新知讲解
新知讲解
例1、 在学校开展“劳动创造美好生活”主题系列活动中,七年级(1)班负责校园某绿化角的设计、种植与养护.
同学们计划将预算经费390元全部用于购买绿萝和吊兰两种绿植,根据设计3盆绿萝数配2盆吊兰。已知绿萝每盆9元,吊兰每盆6元,问可购买绿萝和吊兰各多少盆?
分析:
3盆绿萝配2盆吊兰
绿萝盆数 :吊兰盆数=3 :2
预算经费390元全部用于购买绿萝和吊兰
绿萝费用+吊兰费用 = 390
解:可购买绿萝3x盆,吊兰盆数2x盆,由题意可得
9×3x+6×2x=390
解方程得 x=10
3x=30(盆)
2x=30(盆)
答:可买绿萝30盆,吊兰20盆
分配问题是较复杂的应用题之一
常见的两种基本相等关系:
(1) 总量=各部分量的和;
(2) 表示同一个量的两个不同的式子相等.
设问题中的多个未知量的其中一个为x,利用与未知量密切相关的一个等量关系式表示出另一个未知量,最后利用另外一个等量关系列出方程。
新知总结
成人票数+学生票数=1000张 ①
成人票款+学生票款=6950元 ②
例2、某文艺团为“希望工程”募捐组织了一场义演,共售出1 000张票,筹得票款6 950元.成人票与学生票各售出多少张?
讨论:上面的问题中包含哪些等量关系?
例题精讲
设售出的学生票为x张,填写下表:
学生 成人
票数/张
票款/元
x
1000-x
5x
8(1000-x)
根据等量关系②,列出方程并求解
例2、某文艺团为“希望工程”募捐组织了一场义演,共售出1 000张票,筹得票款6 950元.成人票与学生票各售出多少张?
解:设售出的学生票为x张,由题意得:
5x+8(1000-x)=6950
解这个方程,得x=350.
1000-x=1000-350=650(张)
答:售出成人票650张,学生票350张.
例2、某文艺团为“希望工程”募捐组织了一场义演,共售出1 000张票,筹得票款6 950元.成人票与学生票各售出多少张?
讨论:设所得的学生票款为y元,填写下表:
学生 成人
票数/张
票款/元
6950-y
y
根据等量关系①
,列出方程并求解
解:设所得的学生票款为y元,由题意得:
解这个方程,
得 y=1750.
(张)
(张)
答:售出成人票650张,学生票350张.
想 一 想
因为票的数量为整数张,所以所得票款不可能是6930元.
如果票价不变,售出1000张票后所得票款可能是 6930 元吗? 为什么?
解:设售出学生票x张,由题意得
例2、某文艺团为“希望工程”募捐组织了一场义演,共售出1 000张票,筹得票款6 950元.成人票与学生票各售出多少张?
1、兄弟两人合伙从事经营,哥哥入股25000元,弟弟入股20000元,一年后盈利8352元.按入股的资金比例分配,兄弟两人各应分得盈利多少元?
解方程得
x=4640
8352-x=3712
答:哥哥应分得盈利4640元,
弟弟应分得盈利3712元.
课堂练习
解:设哥哥分得盈利x元,弟弟分得剩下的盈利(8352-x)元.由题意得
x:(8352-x)=25000:20000
2、 某县矿山机械设备闻名省内外.在某矿山机械设备车间工人正在紧张地按订单进度进行生产,若每人每天平均可以生产轴承12个或者轴杆16个,1个轴承与2个轴杆组成一套,该车间共有90人,应该怎样调配人力,才能使每天生产的轴承和轴杆正好配套?
轴杆总数=轴承总数的2倍
等量关系
解:设生产轴承有x人,生产轴杆(90-x)人,由题意可得
16(90-x) =2×12x
x=36
90-x=54(人)
1个轴承与2个轴杆组成一套
答:生产轴承有36人,生产轴杆54人,正好配套
课堂练习
3.某商店今年共销售21英寸(54cm)、25英寸(64cm)、29英寸(74cm)3种彩电360台,它们的销售数量的比是1:7:4,这3种彩各销售了多少台?
课堂练习
分析:这个问题中数量之间的相等关系是:
21英寸的销售数量+25英寸的销售数量+29英寸的销售数量=360
解:设21英寸的彩电销售了x台.
根据题意,得x+7x+4x=360.
解这个方程,得x=30.
答:这3种彩电各销售了30、210、120台.
拓展延伸
1、我国古代数学著作《孙子算经》中有这样一道题,原文如下:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽,问:城中家几何?
大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家共取一头,恰好取完,问:城中有多少户人家?在这个问题中,城中人家的户数为( )
A.25 B. 75 C.81 D.90
B
提示:
城中人家的户数=剩下的鹿的3倍
2、 我国古代《算法统宗》里有这样一首诗:“我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.”
诗中后面两句的意思是:如果一间客房住7人,那么有7人无房可住;如果一间客房住9人,那么就空出一间客房,若设该店有客房x间,可列出关于x的一元一次方程 。
拓展延伸
7x+7=9(x-1)
提示:
客人总数一个量两种表达
课堂小结
列方程解应用题的步骤:
(1)审题,找等量关系
(2)设未知数
(3)列方程
(4)解方程
(5)写出答案
在和、差、倍、分问题中,
量与量之间都存在着关系式:
表示同一个量的两个不同的式子相等
各分量之和=总量.
1、《九章算术》是我国古代的数学专著,几名学生要凑钱购买1本.若每人出8元,则多了3元;若每人出7元,则少了4元.问学生人数和该书单价各是多少?
补充练习
2、某班学生分两组参加植树活动,甲组有17人,乙组有25人,后来由于需要,从甲组抽调了部分学生去乙组,结果乙组的人数是甲组的2倍,从甲组抽调了多少学生去乙组?
补充练习
3、明代数学家程大位所著的《算法统宗》中有这样一个问题:“隔墙听得客分银,不知人数不知银.七两分之多四两,九两分之少半斤.”其大意为:有一群人分银子,如果每人分七两,则剩余四两;如果每人分九两,则还差八两.请问:所分的银子共有 两. (注:明代时1斤=16两,故有“半斤八两”这个成语)
46
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
