第六单元 盈亏问题(课件)(共13张PPT) 沪教版五年级下册数学
文档属性
| 名称 | 第六单元 盈亏问题(课件)(共13张PPT) 沪教版五年级下册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 530.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 15:15:38 | ||
图片预览




文档简介
(共13张PPT)
第一课时 盈数已知的盈平问题
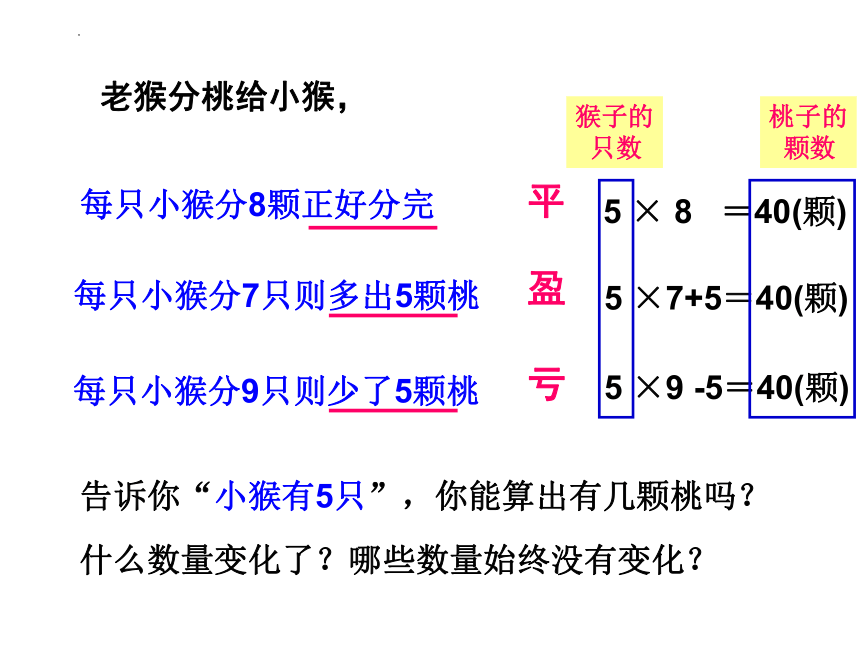
老猴分桃给小猴,
每只小猴分7只则多出5颗桃
每只小猴分9只则少了5颗桃
每只小猴分8颗正好分完
平
盈
亏
告诉你“小猴有5只”,你能算出有几颗桃吗?
5 × 8 =40(颗)
5 ×7+5=40(颗)
5 ×9 -5=40(颗)
猴子的
只数
桃子的
颗数
什么数量变化了?哪些数量始终没有变化?
网球
羽毛球
7
7
4
4
9
两种球取的次数相同
两种球的个数相同
网球总数=羽毛球总数
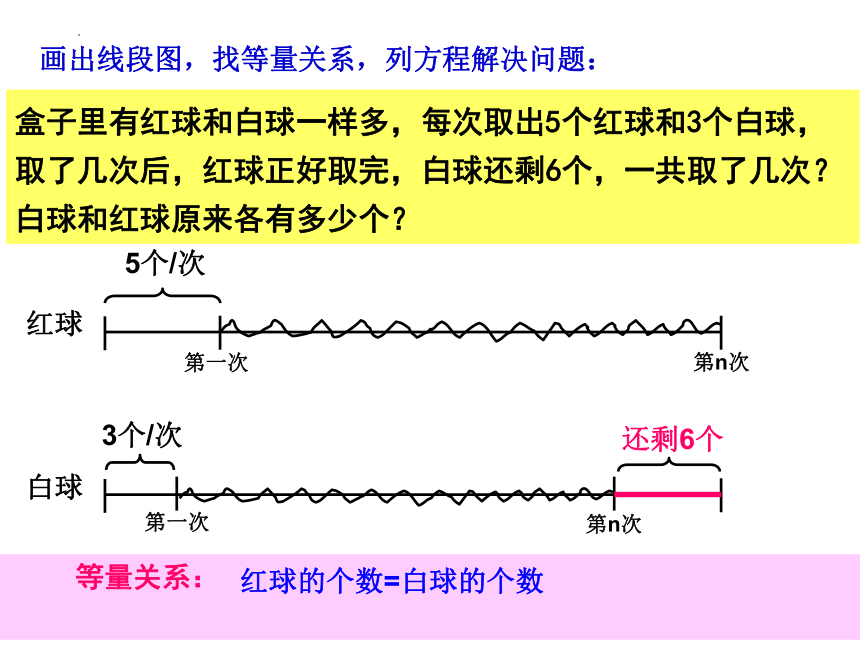
盒子里有红球和白球一样多,每次取出5个红球和3个白球,取了几次后,红球正好取完,白球还剩6个,一共取了几次?白球和红球原来各有多少个?
画出线段图,找等量关系,列方程解决问题:
5个/次
红球
3个/次
白球
第一次
第一次
第n次
第n次
还剩6个
等量关系:
红球的个数=白球的个数
找找等量关系,列方程解决问题。
画线段图,找等量关系,列方程解决问题:
9人/条
方案1
12人/条
方案2
第一条
第一条
第n条
第(n-1)条
同学们去湖边坐船。如果每条船坐9人,那么租的这些船正好
坐满;如果每条船坐12人,那么多出一条船。原来要租多少
条船?一共有几位同学?
等量关系:
1.方案1坐船的人数=方案2坐船的人数
2.方案1船的条数—1 =方案2船的条数
画线段图,找等量关系,列方程解决问题:
一所学校给住宿学生分配宿舍。如果每间宿舍住6人,那么
正好住满;如果每间宿舍住4人,那么正好缺12间宿舍。学
生宿舍有多少间?住宿学生有多少人?
6人/间
方案1
4人/间
方案2
第一间
第一间
第n间
第(n+12)间
等量关系:
1.方案1学生人数=方案2学生人数
2.方案1需要的宿舍间数+12 =方案2需要的宿舍间数
白练:P25/B
1.“中国红十字会”要运一批生活用品到贫困地区,如果每辆车装5000千克,那么这批货物正好装完;如果每辆车装6500千克,那么可以少派6辆车。这批生活用品一共有多少吨?
想一想:线段图怎样画?
5000千克/次
方案1
6500千克/次
方案2
第一辆
第一辆
第n辆
第(n—6)辆
等量关系:
2. 方案1需要车的辆数—6辆=方案2需要车的辆数
1.方案1运货物的重量=方案2运货物的重量
设哪个未知量比较方便?
白练:P25/B
2.小胖每天早晨7时30分从家出发上学。如果每分钟走70米,那么 正好准时到校;如果每分钟走60米,那么就会迟到5分钟。小胖如果每分钟走70米,8时能到达学校吗?
想一想:线段图怎样画?
70米/分
方案1
60米/分
方案2
第一分钟
第一分钟
第n分钟
第(n+5)分钟
等量关系:
2. 方案1用的时间+5分钟=方案2用的时间
1.方案1小胖行的路程=方案2小胖行的路程
设哪个未知量比较方便?
小巧包装糖果。如果每袋装40粒,则剩下5粒。如果每袋多包2粒,恰好多余了一个包装袋。一共有几个包装袋?有多少粒糖?
动脑筋:你能借助线段图理解题意,解决问题吗?
40粒/袋
方案1
(40+2)粒/袋
方案2
第一袋
第一袋
第n袋
第(n—1)袋
等量关系:
2. 方案1用的包装袋个数—1个=方案2用的包装袋个数
1.方案1小巧包装的糖果数=方案2小巧包装的糖果数
剩5粒
7个/次
网球
4个/次
羽毛球
第一次
第一次
第n次
第n次
剩9个
7-4=3(个)
7个/次
9÷(7—4)
=3(次)
第一课时 盈数已知的盈平问题
老猴分桃给小猴,
每只小猴分7只则多出5颗桃
每只小猴分9只则少了5颗桃
每只小猴分8颗正好分完
平
盈
亏
告诉你“小猴有5只”,你能算出有几颗桃吗?
5 × 8 =40(颗)
5 ×7+5=40(颗)
5 ×9 -5=40(颗)
猴子的
只数
桃子的
颗数
什么数量变化了?哪些数量始终没有变化?
网球
羽毛球
7
7
4
4
9
两种球取的次数相同
两种球的个数相同
网球总数=羽毛球总数
盒子里有红球和白球一样多,每次取出5个红球和3个白球,取了几次后,红球正好取完,白球还剩6个,一共取了几次?白球和红球原来各有多少个?
画出线段图,找等量关系,列方程解决问题:
5个/次
红球
3个/次
白球
第一次
第一次
第n次
第n次
还剩6个
等量关系:
红球的个数=白球的个数
找找等量关系,列方程解决问题。
画线段图,找等量关系,列方程解决问题:
9人/条
方案1
12人/条
方案2
第一条
第一条
第n条
第(n-1)条
同学们去湖边坐船。如果每条船坐9人,那么租的这些船正好
坐满;如果每条船坐12人,那么多出一条船。原来要租多少
条船?一共有几位同学?
等量关系:
1.方案1坐船的人数=方案2坐船的人数
2.方案1船的条数—1 =方案2船的条数
画线段图,找等量关系,列方程解决问题:
一所学校给住宿学生分配宿舍。如果每间宿舍住6人,那么
正好住满;如果每间宿舍住4人,那么正好缺12间宿舍。学
生宿舍有多少间?住宿学生有多少人?
6人/间
方案1
4人/间
方案2
第一间
第一间
第n间
第(n+12)间
等量关系:
1.方案1学生人数=方案2学生人数
2.方案1需要的宿舍间数+12 =方案2需要的宿舍间数
白练:P25/B
1.“中国红十字会”要运一批生活用品到贫困地区,如果每辆车装5000千克,那么这批货物正好装完;如果每辆车装6500千克,那么可以少派6辆车。这批生活用品一共有多少吨?
想一想:线段图怎样画?
5000千克/次
方案1
6500千克/次
方案2
第一辆
第一辆
第n辆
第(n—6)辆
等量关系:
2. 方案1需要车的辆数—6辆=方案2需要车的辆数
1.方案1运货物的重量=方案2运货物的重量
设哪个未知量比较方便?
白练:P25/B
2.小胖每天早晨7时30分从家出发上学。如果每分钟走70米,那么 正好准时到校;如果每分钟走60米,那么就会迟到5分钟。小胖如果每分钟走70米,8时能到达学校吗?
想一想:线段图怎样画?
70米/分
方案1
60米/分
方案2
第一分钟
第一分钟
第n分钟
第(n+5)分钟
等量关系:
2. 方案1用的时间+5分钟=方案2用的时间
1.方案1小胖行的路程=方案2小胖行的路程
设哪个未知量比较方便?
小巧包装糖果。如果每袋装40粒,则剩下5粒。如果每袋多包2粒,恰好多余了一个包装袋。一共有几个包装袋?有多少粒糖?
动脑筋:你能借助线段图理解题意,解决问题吗?
40粒/袋
方案1
(40+2)粒/袋
方案2
第一袋
第一袋
第n袋
第(n—1)袋
等量关系:
2. 方案1用的包装袋个数—1个=方案2用的包装袋个数
1.方案1小巧包装的糖果数=方案2小巧包装的糖果数
剩5粒
7个/次
网球
4个/次
羽毛球
第一次
第一次
第n次
第n次
剩9个
7-4=3(个)
7个/次
9÷(7—4)
=3(次)
