华师大版数学九年级上册24.1测量教案(含答案)
文档属性
| 名称 | 华师大版数学九年级上册24.1测量教案(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 141.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-31 00:00:00 | ||
图片预览

文档简介
第24章 解直角三角形
课题 测量
1.复习巩固相似三角形知识,掌握测量方法;
2.通过测量旗杆高度的活动,巩固相似三角形有关知识,累积数学活动经验,使学生初步学会数学建模的方法;
3.通过运用相似以及已学过的知识探索解三角形的方法,体验教学研究和发现的过程,逐渐培养学生用数学说理的习惯,激起学生学习后续内容的积极性.
掌握测量方法.
理解并掌握测量方法.
一、情景导入 感受新知
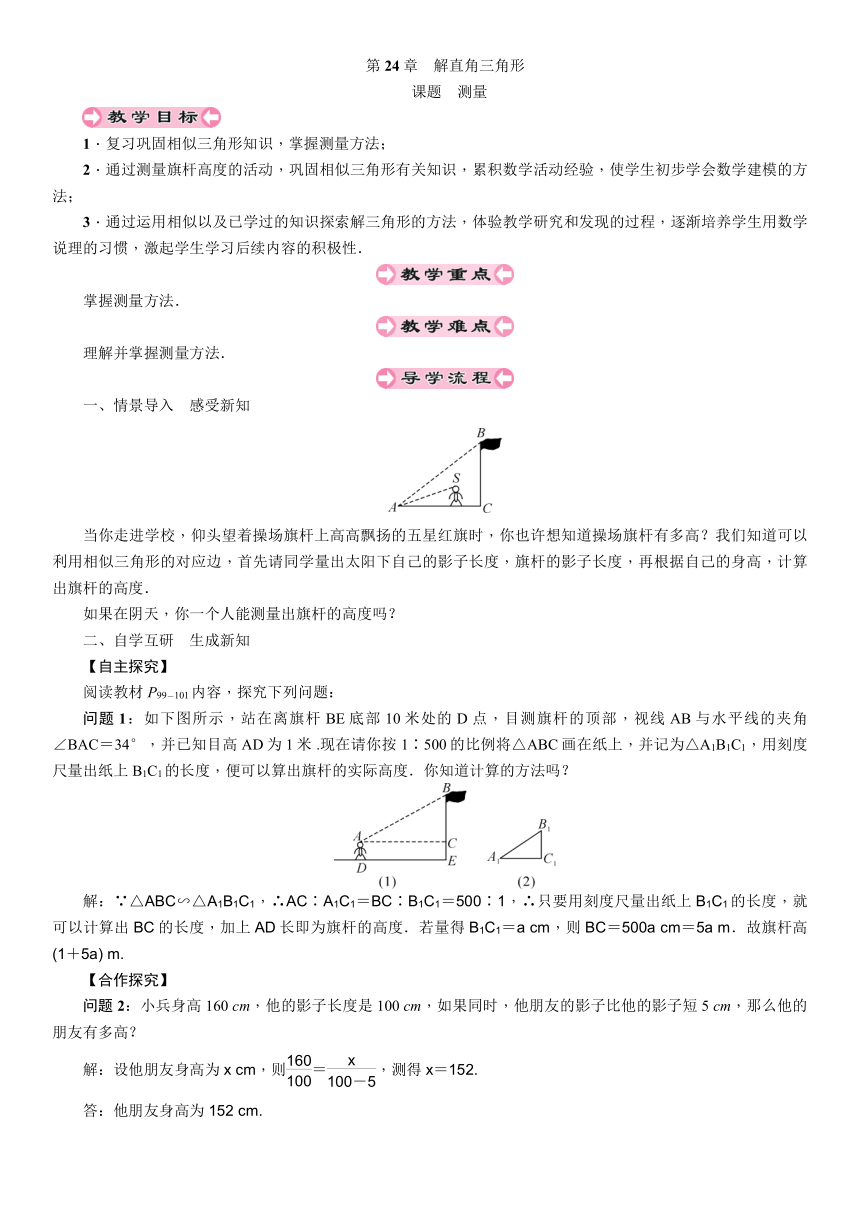
当你走进学校,仰头望着操场旗杆上高高飘扬的五星红旗时,你也许想知道操场旗杆有多高?我们知道可以利用相似三角形的对应边,首先请同学量出太阳下自己的影子长度,旗杆的影子长度,再根据自己的身高,计算出旗杆的高度.
如果在阴天,你一个人能测量出旗杆的高度吗?
二、自学互研 生成新知
【自主探究】
阅读教材P99-101内容,探究下列问题:
问题1:如下图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC=34°,并已知目高AD为1米 .现在请你按1∶500的比例将△ABC画在纸上,并记为△A1B1C1,用刻度尺量出纸上B1C1的长度,便可以算出旗杆的实际高度.你知道计算的方法吗?
解:∵△ABC∽△A1B1C1,∴AC∶A1C1=BC∶B1C1=500∶1,∴只要用刻度尺量出纸上B1C1的长度,就可以计算出BC的长度,加上AD长即为旗杆的高度.若量得B1C1=a cm,则BC=500a cm=5a m.故旗杆高(1+5a) m.
【合作探究】
问题2:小兵身高160 cm,他的影子长度是100 cm,如果同时,他朋友的影子比他的影子短5 cm,那么他的朋友有多高?
解:设他朋友身高为x cm,则=,测得x=152.
答:他朋友身高为152 cm.
问题3:小明想知道学校旗杆的高度,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,求旗杆的高度.
解:设旗杆的高度为x m,则x2+52=(x+1)2,解得x=12.
答:旗杆的高度为12 m.
【师生活动】
①明了学情:关注学生对测量方法与综合运用所学知识解决问题的掌握情况.
②差异指导:对学生在探究中产生的困惑及时引导,点拨.
③生生互助:学生小组内交流讨论,相互释疑,达成共识.
三、典例剖析 运用新知
【合作探究】
【例】如图,小明站在C处看甲乙两楼楼顶上的点A和点E,点C,E,A在同一条直线上,点B,D分别在 E,A的正下方,且点D,B,C在同一条直线上,点B,C相距20米 .点D,C相距40米,乙楼高BE为15米.求甲楼AD的高.(小明的身高忽略不计)
解:由题意知BC=20,CD=40,△CBE∽△CDA.∴=即=,∴AD=30(米).
答:甲楼AD高30米.
【变式迁移】
如图,想测量一建筑物AB的高度,发现该建筑物在阳光下的影子恰好落在斜坡CD和地面BC上,已知CD=2米,BC=6.4米,CD与地面成45°角,同一时刻,身高1.5米的张军影长为1.2米,求该建筑物的高度.
解:在Rt△CDE中,∠DCE=45°,∴DE=CE.由勾股定理CD2=CE2+DE2可得CE=DE=2.∵=,∴EF=1.6.又∵=,即=,∴AB=12.5(米).
故该建筑物的高度是12.5米.
四、课堂小结 回顾新知
通过本节课的学习,你有了哪些新的收获?还存在哪些疑问?请谈一谈你的想法,与同学们一起分享.
五、检测反馈 落实新知
1.某同学要测量树的高度,在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示.若此时落在地面上的影长为4.4米,则树高为(C)
A.11.5米 B.11.75米
C.11.8米 D.12.25米
2.如图所示,有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了__10__米.
六、课后作业 巩固新知
见学生用书.
课题 测量
1.复习巩固相似三角形知识,掌握测量方法;
2.通过测量旗杆高度的活动,巩固相似三角形有关知识,累积数学活动经验,使学生初步学会数学建模的方法;
3.通过运用相似以及已学过的知识探索解三角形的方法,体验教学研究和发现的过程,逐渐培养学生用数学说理的习惯,激起学生学习后续内容的积极性.
掌握测量方法.
理解并掌握测量方法.
一、情景导入 感受新知
当你走进学校,仰头望着操场旗杆上高高飘扬的五星红旗时,你也许想知道操场旗杆有多高?我们知道可以利用相似三角形的对应边,首先请同学量出太阳下自己的影子长度,旗杆的影子长度,再根据自己的身高,计算出旗杆的高度.
如果在阴天,你一个人能测量出旗杆的高度吗?
二、自学互研 生成新知
【自主探究】
阅读教材P99-101内容,探究下列问题:
问题1:如下图所示,站在离旗杆BE底部10米处的D点,目测旗杆的顶部,视线AB与水平线的夹角∠BAC=34°,并已知目高AD为1米 .现在请你按1∶500的比例将△ABC画在纸上,并记为△A1B1C1,用刻度尺量出纸上B1C1的长度,便可以算出旗杆的实际高度.你知道计算的方法吗?
解:∵△ABC∽△A1B1C1,∴AC∶A1C1=BC∶B1C1=500∶1,∴只要用刻度尺量出纸上B1C1的长度,就可以计算出BC的长度,加上AD长即为旗杆的高度.若量得B1C1=a cm,则BC=500a cm=5a m.故旗杆高(1+5a) m.
【合作探究】
问题2:小兵身高160 cm,他的影子长度是100 cm,如果同时,他朋友的影子比他的影子短5 cm,那么他的朋友有多高?
解:设他朋友身高为x cm,则=,测得x=152.
答:他朋友身高为152 cm.
问题3:小明想知道学校旗杆的高度,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,求旗杆的高度.
解:设旗杆的高度为x m,则x2+52=(x+1)2,解得x=12.
答:旗杆的高度为12 m.
【师生活动】
①明了学情:关注学生对测量方法与综合运用所学知识解决问题的掌握情况.
②差异指导:对学生在探究中产生的困惑及时引导,点拨.
③生生互助:学生小组内交流讨论,相互释疑,达成共识.
三、典例剖析 运用新知
【合作探究】
【例】如图,小明站在C处看甲乙两楼楼顶上的点A和点E,点C,E,A在同一条直线上,点B,D分别在 E,A的正下方,且点D,B,C在同一条直线上,点B,C相距20米 .点D,C相距40米,乙楼高BE为15米.求甲楼AD的高.(小明的身高忽略不计)
解:由题意知BC=20,CD=40,△CBE∽△CDA.∴=即=,∴AD=30(米).
答:甲楼AD高30米.
【变式迁移】
如图,想测量一建筑物AB的高度,发现该建筑物在阳光下的影子恰好落在斜坡CD和地面BC上,已知CD=2米,BC=6.4米,CD与地面成45°角,同一时刻,身高1.5米的张军影长为1.2米,求该建筑物的高度.
解:在Rt△CDE中,∠DCE=45°,∴DE=CE.由勾股定理CD2=CE2+DE2可得CE=DE=2.∵=,∴EF=1.6.又∵=,即=,∴AB=12.5(米).
故该建筑物的高度是12.5米.
四、课堂小结 回顾新知
通过本节课的学习,你有了哪些新的收获?还存在哪些疑问?请谈一谈你的想法,与同学们一起分享.
五、检测反馈 落实新知
1.某同学要测量树的高度,在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示.若此时落在地面上的影长为4.4米,则树高为(C)
A.11.5米 B.11.75米
C.11.8米 D.12.25米
2.如图所示,有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了__10__米.
六、课后作业 巩固新知
见学生用书.
