3.1.1 探索勾股定理同步练习(含解析)
文档属性
| 名称 | 3.1.1 探索勾股定理同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 22:41:09 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第三章 勾股定理
1 探索勾股定理
第1课时 探索勾股定理
基础夯实
知识点一 勾股定理
1.长方形的一条对角线的长为 10 cm,一边长为 6 cm,它的面积是( )
A.24 cm B.48 cm C.60 cm D.64 cm
2.等腰三角形的底边长为 6,底边上的中线长为4,它的腰长为( )
A.7 B.6 C.5 D.4
3.在 Rt△ABC中,∠C=90°,若a=5,b=12,则c=____________.
4.如果梯子的底端离建筑物 5米,那么13米长的梯子可以达到该建筑物 的 高度是____________米.
5.如图,在 Rt△ABC 中,∠C=90°.
(1)若AC=5,BC=12,求 AB 的长;
(2)若 AB=25,AC=20,求 BC的长.
知识点二 利用勾股定理求面积
6.如图,两个较大正方形的面积分别为 225,289,则字母A 所代表的正方形的面积为( )
A.4 B.8 C.16 D.64
第6题图 第7题图
7.如图,点 E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48 B.60 C.76 D.80
8.已知直角三角形的三边长为 6,8,x,则以x为边的正方形的面积为( )
A.28 B.100 C.64 D.28 或100
9.如图,分别以 Rt△ABC三边为直径向外作三个半圆,其面积分别用 S ,S ,S 表示.已知 求 S 的大小.
易错点 考虑不全而漏解
10.若一个直角三角形的三边长分别为 a,b,c,已知a =25,b =144,则c =( )
A.169 B.119 C.13 或25 D.169 或119
能力提升
11.如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形A,C,D的面积依次为4,6,18,则正方形B的面积为( )
A.8 B.9 C.10 D.12
第11题图 第12题图
12.如图,Rt△ABC中,∠B=90°,AB=3cm,AC=5cm ,将△ABC折叠,使点C与A重合,得折痕 DE,则△ABE 的周长等于_____________cm.
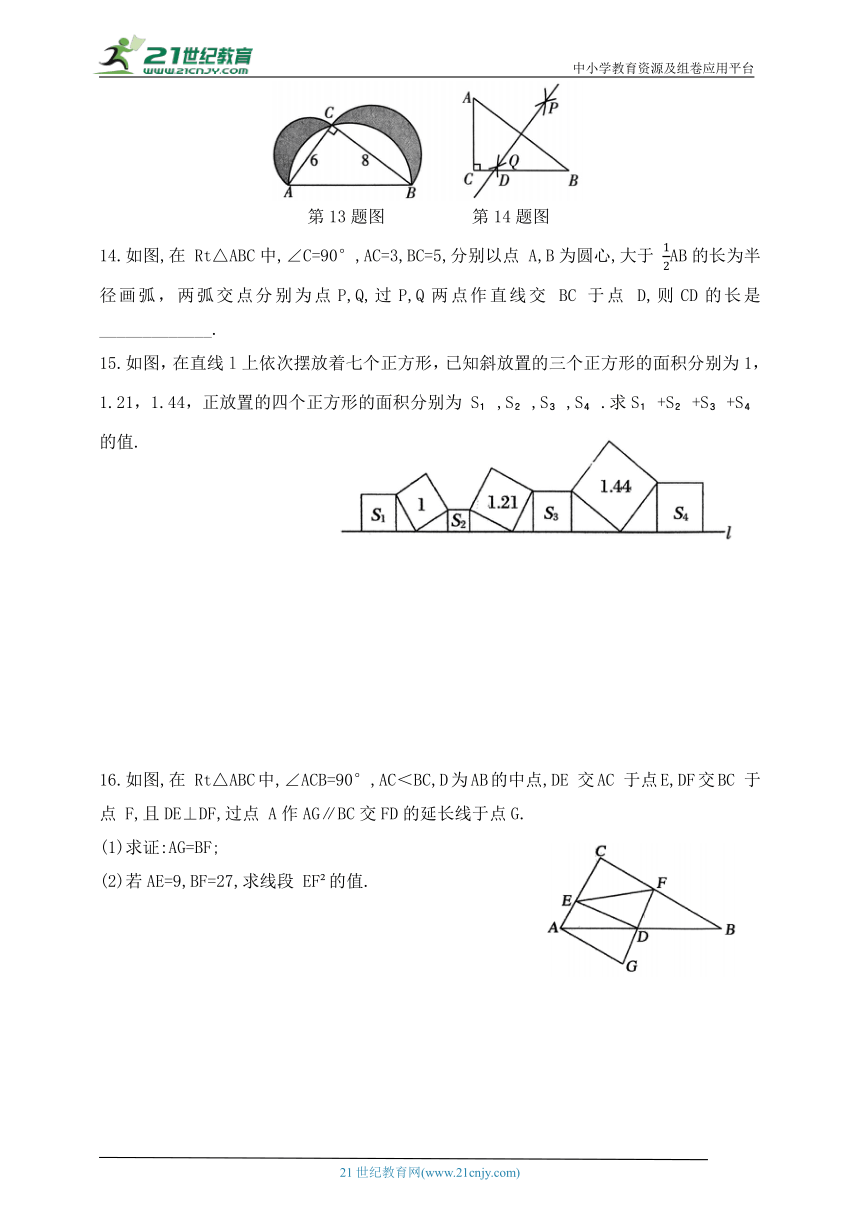
13.如图,在 Rt△ABC 中,AC=6,BC=8,分别以它的三边为直径作三个半圆,则阴影部分的面积为____________.
第13题图 第14题图
14.如图,在 Rt△ABC中,∠C=90°,AC=3,BC=5,分别以点 A,B为圆心,大于 AB的长为半径画弧,两弧交点分别为点P,Q,过P,Q两点作直线交 BC 于点 D,则CD的长是_____________.
15.如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,1.21,1.44,正放置的四个正方形的面积分别为 S ,S ,S ,S .求S +S +S +S
的值.
16.如图,在 Rt△ABC中,∠ACB=90°,AC<BC,D为AB的中点,DE 交AC 于点E,DF交BC 于点 F,且DE⊥DF,过点 A作AG∥BC交FD的延长线于点G.
(1)求证:AG=BF;
(2)若AE=9,BF=27,求线段 EF 的值.
核心拓展
17.如图所示是一种“羊头”形图案,其作法是:从正方形①开始,以它的一条边为斜边作等腰直角三角形,然后再以这个等腰直角三角形两直角边为边作正方形②和②′,如此继续下去,…,若正方形①的面积为 64,则正方形⑥的面积为____________.
参考答案
1. B 【解析】由勾股定理可得长方形的另一条边长为8cm,所以长方形的面积为6×8=48(cm ).故选B.
2. C 3.13 4.12
5.解:(1)在 Rt△ABC中,∠C=90°,由勾股定理,得AC +BC =AB ,即5 +12 =169=AB .
所以AB=13.
(2)在 Rt△ABC中,∠C=90°,由勾股定理,得AC +BC =AB .
即20 +BC =25 ,BC =25 -20 =225.所以BC=15.
6. D 7. C
8. D【解析】x可能是直角边长,也可能是斜边长,因此需分两种情况讨论.两种情况利用勾股定理可获解.
9.解:
同理,得
又根据勾股定理,得AC +BC =AB ,
所以 即S +S =S .
所以
10. D【解析】由于未知c为斜边还是直角边,故分两种情况讨论:
当c为斜边时,c =a +b =25+144=169;
当c为直角边时,c =b -a =144-25=119.
11. A 【解析】由勾股定理得正方形E的面积=18-6=12,正方形B的面积=12-4=8.故选 A.
12.7 【解析】根据勾股定理,得BC=4 cm. 由折叠知AE=CE,所以△ABE的周长=AB+BE+AE=AB+BE+CE=AB+BC=7 cm.
13.24【解析】设分别以AC,AB,BC为直径的半圆的面积分别为S ,S ,S ,则有结论S +S =S ,阴影部分的面积为
【解析】如图,连接AD,由作图可知PQ垂直平分AB,所以AD= BD.设 CD=x,则 AD=BD=5-x.在Rt△ACD中,因为AC +CD =AD ,即9+x =(5-x) ,解得
15.解:如图,易知相邻的两个直角三角形全等,即△ACB≌△BDE(AAS),所以 BC=ED,AC=BD.
根据勾股定理的几何意义可知:S +S =1.
同理:S +S =1.44.所以S +S +S +S =2.44.
16.(1)证明:因为D是AB 的中点,所以AD=BD.
因为AG∥BC,所以∠GAD=∠FBD.
因为∠ADG=∠BDF.所以△ADG≌△BDF(ASA).所以AG=BF.
(2)解:如图,连接 EG.
因为△ADG≌△BDF,所以GD=FD.
因为DE⊥DF,所以EG=EF.
因为AG∥BC,∠ACB=90°,所以∠EAG=90°.
在 Rt△EAG中,因为EG =AE +AG =AE +BF ,所以EF =AE +BF .因为AE=9,BF=27.
所以EF =810.
17.2 【解析】由题意及勾股定理可知,正方形②面积的2倍等于正方形①的面积,故正方形②面积为32,以此类推,正方形③面积为 16,…,正方形n的面积为 故正方形⑥的面积为2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 勾股定理
1 探索勾股定理
第1课时 探索勾股定理
基础夯实
知识点一 勾股定理
1.长方形的一条对角线的长为 10 cm,一边长为 6 cm,它的面积是( )
A.24 cm B.48 cm C.60 cm D.64 cm
2.等腰三角形的底边长为 6,底边上的中线长为4,它的腰长为( )
A.7 B.6 C.5 D.4
3.在 Rt△ABC中,∠C=90°,若a=5,b=12,则c=____________.
4.如果梯子的底端离建筑物 5米,那么13米长的梯子可以达到该建筑物 的 高度是____________米.
5.如图,在 Rt△ABC 中,∠C=90°.
(1)若AC=5,BC=12,求 AB 的长;
(2)若 AB=25,AC=20,求 BC的长.
知识点二 利用勾股定理求面积
6.如图,两个较大正方形的面积分别为 225,289,则字母A 所代表的正方形的面积为( )
A.4 B.8 C.16 D.64
第6题图 第7题图
7.如图,点 E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48 B.60 C.76 D.80
8.已知直角三角形的三边长为 6,8,x,则以x为边的正方形的面积为( )
A.28 B.100 C.64 D.28 或100
9.如图,分别以 Rt△ABC三边为直径向外作三个半圆,其面积分别用 S ,S ,S 表示.已知 求 S 的大小.
易错点 考虑不全而漏解
10.若一个直角三角形的三边长分别为 a,b,c,已知a =25,b =144,则c =( )
A.169 B.119 C.13 或25 D.169 或119
能力提升
11.如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,若正方形A,C,D的面积依次为4,6,18,则正方形B的面积为( )
A.8 B.9 C.10 D.12
第11题图 第12题图
12.如图,Rt△ABC中,∠B=90°,AB=3cm,AC=5cm ,将△ABC折叠,使点C与A重合,得折痕 DE,则△ABE 的周长等于_____________cm.
13.如图,在 Rt△ABC 中,AC=6,BC=8,分别以它的三边为直径作三个半圆,则阴影部分的面积为____________.
第13题图 第14题图
14.如图,在 Rt△ABC中,∠C=90°,AC=3,BC=5,分别以点 A,B为圆心,大于 AB的长为半径画弧,两弧交点分别为点P,Q,过P,Q两点作直线交 BC 于点 D,则CD的长是_____________.
15.如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,1.21,1.44,正放置的四个正方形的面积分别为 S ,S ,S ,S .求S +S +S +S
的值.
16.如图,在 Rt△ABC中,∠ACB=90°,AC<BC,D为AB的中点,DE 交AC 于点E,DF交BC 于点 F,且DE⊥DF,过点 A作AG∥BC交FD的延长线于点G.
(1)求证:AG=BF;
(2)若AE=9,BF=27,求线段 EF 的值.
核心拓展
17.如图所示是一种“羊头”形图案,其作法是:从正方形①开始,以它的一条边为斜边作等腰直角三角形,然后再以这个等腰直角三角形两直角边为边作正方形②和②′,如此继续下去,…,若正方形①的面积为 64,则正方形⑥的面积为____________.
参考答案
1. B 【解析】由勾股定理可得长方形的另一条边长为8cm,所以长方形的面积为6×8=48(cm ).故选B.
2. C 3.13 4.12
5.解:(1)在 Rt△ABC中,∠C=90°,由勾股定理,得AC +BC =AB ,即5 +12 =169=AB .
所以AB=13.
(2)在 Rt△ABC中,∠C=90°,由勾股定理,得AC +BC =AB .
即20 +BC =25 ,BC =25 -20 =225.所以BC=15.
6. D 7. C
8. D【解析】x可能是直角边长,也可能是斜边长,因此需分两种情况讨论.两种情况利用勾股定理可获解.
9.解:
同理,得
又根据勾股定理,得AC +BC =AB ,
所以 即S +S =S .
所以
10. D【解析】由于未知c为斜边还是直角边,故分两种情况讨论:
当c为斜边时,c =a +b =25+144=169;
当c为直角边时,c =b -a =144-25=119.
11. A 【解析】由勾股定理得正方形E的面积=18-6=12,正方形B的面积=12-4=8.故选 A.
12.7 【解析】根据勾股定理,得BC=4 cm. 由折叠知AE=CE,所以△ABE的周长=AB+BE+AE=AB+BE+CE=AB+BC=7 cm.
13.24【解析】设分别以AC,AB,BC为直径的半圆的面积分别为S ,S ,S ,则有结论S +S =S ,阴影部分的面积为
【解析】如图,连接AD,由作图可知PQ垂直平分AB,所以AD= BD.设 CD=x,则 AD=BD=5-x.在Rt△ACD中,因为AC +CD =AD ,即9+x =(5-x) ,解得
15.解:如图,易知相邻的两个直角三角形全等,即△ACB≌△BDE(AAS),所以 BC=ED,AC=BD.
根据勾股定理的几何意义可知:S +S =1.
同理:S +S =1.44.所以S +S +S +S =2.44.
16.(1)证明:因为D是AB 的中点,所以AD=BD.
因为AG∥BC,所以∠GAD=∠FBD.
因为∠ADG=∠BDF.所以△ADG≌△BDF(ASA).所以AG=BF.
(2)解:如图,连接 EG.
因为△ADG≌△BDF,所以GD=FD.
因为DE⊥DF,所以EG=EF.
因为AG∥BC,∠ACB=90°,所以∠EAG=90°.
在 Rt△EAG中,因为EG =AE +AG =AE +BF ,所以EF =AE +BF .因为AE=9,BF=27.
所以EF =810.
17.2 【解析】由题意及勾股定理可知,正方形②面积的2倍等于正方形①的面积,故正方形②面积为32,以此类推,正方形③面积为 16,…,正方形n的面积为 故正方形⑥的面积为2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
