3.1.2 验证勾股定理及其计算同步练习(含解析)
文档属性
| 名称 | 3.1.2 验证勾股定理及其计算同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 22:42:06 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第三章 勾股定理
1 探索勾股定理
第2课时 验证勾股定理及其计算
基础夯实
知识点一 勾股定理的验证
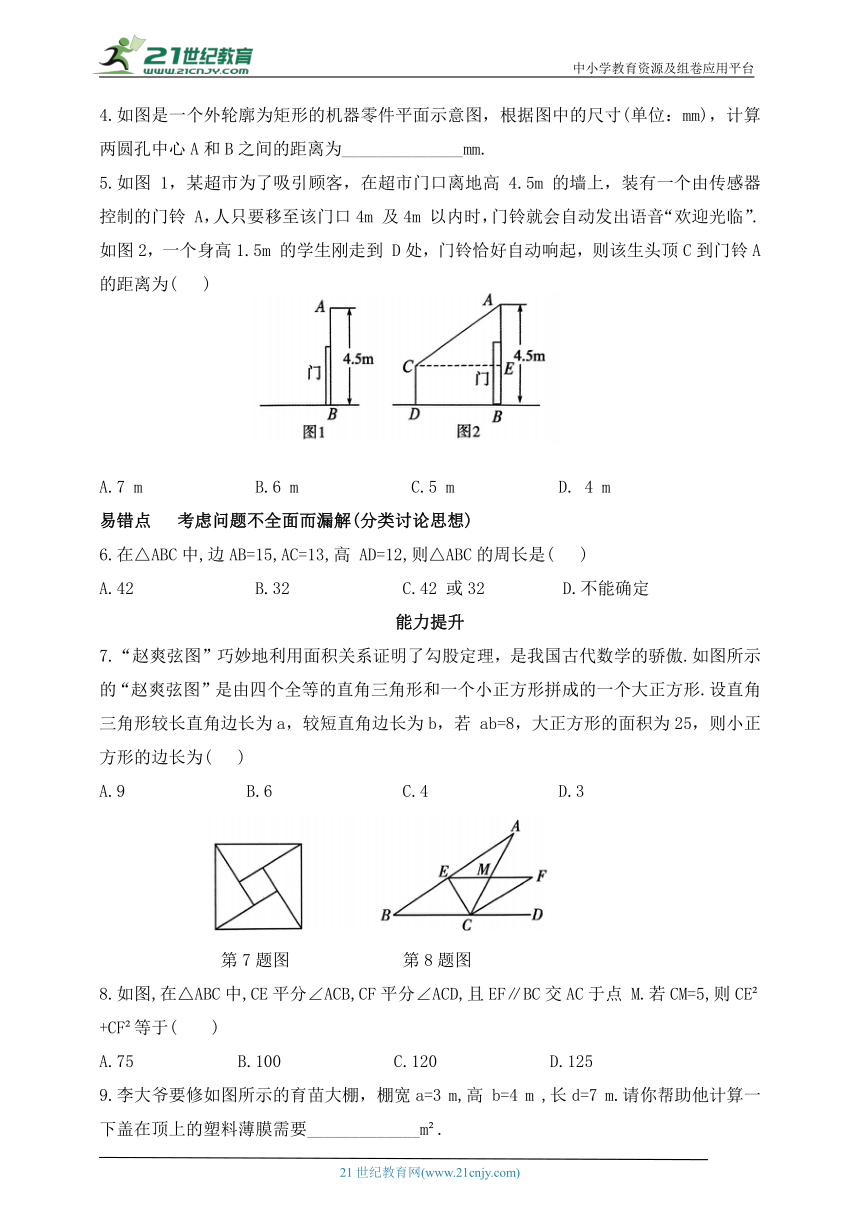
1.下列选项中,不能用来证明勾股定理的是( )
2.将四块全等的直角三角形纸板分别拼成如图1、图2 所示的正方形.请通过由图 1到图2的转换,证明勾股定理.
知识点二 勾股定理的有关计算
3.如图,有一块边长为24米的正方形绿地,在绿地旁边 B处有健身器材,由于居住在 A 处的居民践踏了绿地,小明想在 A 处树立一个标牌“少走◇米,踏之何忍 ”请你计算后帮小明在标牌的“◇”处填上适当的数字,应为( )
A.3 B.4 C.5 D.6
第3题图 第4题图
4.如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算两圆孔中心A和B之间的距离为______________mm.
5.如图 1,某超市为了吸引顾客,在超市门口离地高 4.5m 的墙上,装有一个由传感器控制的门铃 A,人只要移至该门口4m 及4m 以内时,门铃就会自动发出语音“欢迎光临”.如图2,一个身高1.5m 的学生刚走到 D处,门铃恰好自动响起,则该生头顶C到门铃A 的距离为( )
A.7 m B.6 m C.5 m D. 4 m
易错点 考虑问题不全面而漏解(分类讨论思想)
6.在△ABC中,边AB=15,AC=13,高 AD=12,则△ABC的周长是( )
A.42 B.32 C.42 或32 D.不能确定
能力提升
7.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若 ab=8,大正方形的面积为25,则小正方形的边长为( )
A.9 B.6 C.4 D.3
第7题图 第8题图
8.如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于点 M.若CM=5,则CE +CF 等于( )
A.75 B.100 C.120 D.125
9.李大爷要修如图所示的育苗大棚,棚宽a=3 m,高 b=4 m ,长d=7 m.请你帮助他计算一
下盖在顶上的塑料薄膜需要_____________m .
第9题图 第10题图
10.如图是一幅赵爽弦图,利用此图可以证明勾股定理.现连接 BE,发现 AB=BE,若DE = 1,则 正 方形 ABCD 的面积为______________.
11.已知直角三角形的两直角边长分别为 5cm和12 cm,则斜边上的高为___________cm.
12.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子 BC 的长为17米,几分钟后船到达点 D的位置,此时绳子CD的长为 10米,问船向岸边移动了__________米.
13.四个全等的直角三角形的直角边分别为 a,b,斜边为 c.现把它们适当拼合,可以得到如图的图形.利用这个图形可以验证勾股定理,你能说明其中的道理吗 请试一试.
核心拓展
14.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪灵感.他惊喜地发现:当两个全等的直角三角形如图1或图 2 摆放时,都可以用“面积法”来证明.下面是小聪利用图 1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a +b =c .
证明:连接 DB,过点 D作 BC 边上的高DF,DF=EC=b-a.
因为
且
所以
所以a +b =c .
请参照上述证法,利用图 2 完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a +b =c .
证明:连接___________________________.
因为_______________________________________________________,
且 ________________________________________________________,
所以___________________________________________________________________.
所以a +b =c .
参考答案
1. D【解析】选项A 可以利用面积的关系式 a) =c 来验证勾股定理;选项 B可以利用面积的关系式 来验证勾股定理;选项C可以利用
面积的关系式 来验证勾股定理;选项 D无法验证勾股定理.
2.解:因为图1与图 2 拼出的大正方形面积相等,所以两个大正方形中空白部分的面积相等,所以c =b +a ,即a +b =c .
3. D【解析】由勾股定理,得AB=25,因此,少走的路程为24+7-25=6(米).
4.150 【解析】AC=150-60=90(mm),BC=180-60=120(mm),根据勾股定理,得AB =AC +BC =90 +120 =150 .所以AB=150mm.
5. C【解析】由题意可知:BE=CD=1.5m ,AE=AB-BE=4.5-1.5=3(m),CE=4m,
由勾股定理,得AC=5m .故选C.
6. C【解析】由于已知条件中△ABC 形状未确定,故分两种情况讨论.
当△ABC为锐角三角形时(如图1),即高AD在△ABC 内部,在 Rt△ABD中,AD =AB -BD ,即12 =15 -BD ,BD =81,所以BD=9,在Rt△ACD中,CD =AC -AD =13 -12 =25.所以CD=5.所以BC=9+5=14.△ABC的周长=15+13+14=42;当△ABC为钝角三角形时(如图2),即高AD在△ABC外部,此时BC=BD-CD=9-5=4,所以△ABC周长=15+13+4=32.
7. D【解析】设直角三角形斜边长为c,根据勾股定理,得a +b =c =25.因为 ab=8,所以(a-b) =a +b -2ab=25-2×8=9,即a-b=3,即小正方形的边长为3.
8. B 【解析】根据题意,得∠ECF=∠ACE+∠ACF= 所以△EFC为直角三角形.因为EF∥BC,CE平分∠ACB,CF平分∠ACD,所以∠ECB=∠MEC=∠ECM,∠DCF=∠CFM=∠MCF.所以EM=CM=MF=5,所以EF=10.在Rt△EFC中,由勾股定理,得CE +CF =EF =100.
9.35 【解析】由勾股定理可得直角三角形的斜边长为5m,所以所需长方形塑料薄膜的面积是5×7=35(m ).
10.5 【解析】如图,由题意,得AH=DE=1.
因为AB=BE,BH⊥AE,所以AE=2AH=2.
所以正方形ABCD的面积=AD =5.
11. 【解析】因为直角三角形的两直角边长分别为5cm 和12cm,所以斜边长的平方=5 +12 =13 .所以斜边=13cm.设斜边上的高为xcm,则 解得 即斜边上的高为
12.9 【解析】在 Rt△ABC中,
因为∠CAB=90°,BC=17米,AC=8米,所以AB =BC -AC =17 -8 =225.
所以AB=15米.同理可求AD=6米.所以BD=AB-AD=15-6=9(米),即船向岸边移动了9米.
13.解:图形的总面积可以表示为
也可以表示为 所以c +ab=a +b +ab.即a +b =c .
14.解:依次填写:
BD,过点 B作DE边上的高BF,则BF=b-a
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 勾股定理
1 探索勾股定理
第2课时 验证勾股定理及其计算
基础夯实
知识点一 勾股定理的验证
1.下列选项中,不能用来证明勾股定理的是( )
2.将四块全等的直角三角形纸板分别拼成如图1、图2 所示的正方形.请通过由图 1到图2的转换,证明勾股定理.
知识点二 勾股定理的有关计算
3.如图,有一块边长为24米的正方形绿地,在绿地旁边 B处有健身器材,由于居住在 A 处的居民践踏了绿地,小明想在 A 处树立一个标牌“少走◇米,踏之何忍 ”请你计算后帮小明在标牌的“◇”处填上适当的数字,应为( )
A.3 B.4 C.5 D.6
第3题图 第4题图
4.如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算两圆孔中心A和B之间的距离为______________mm.
5.如图 1,某超市为了吸引顾客,在超市门口离地高 4.5m 的墙上,装有一个由传感器控制的门铃 A,人只要移至该门口4m 及4m 以内时,门铃就会自动发出语音“欢迎光临”.如图2,一个身高1.5m 的学生刚走到 D处,门铃恰好自动响起,则该生头顶C到门铃A 的距离为( )
A.7 m B.6 m C.5 m D. 4 m
易错点 考虑问题不全面而漏解(分类讨论思想)
6.在△ABC中,边AB=15,AC=13,高 AD=12,则△ABC的周长是( )
A.42 B.32 C.42 或32 D.不能确定
能力提升
7.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若 ab=8,大正方形的面积为25,则小正方形的边长为( )
A.9 B.6 C.4 D.3
第7题图 第8题图
8.如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于点 M.若CM=5,则CE +CF 等于( )
A.75 B.100 C.120 D.125
9.李大爷要修如图所示的育苗大棚,棚宽a=3 m,高 b=4 m ,长d=7 m.请你帮助他计算一
下盖在顶上的塑料薄膜需要_____________m .
第9题图 第10题图
10.如图是一幅赵爽弦图,利用此图可以证明勾股定理.现连接 BE,发现 AB=BE,若DE = 1,则 正 方形 ABCD 的面积为______________.
11.已知直角三角形的两直角边长分别为 5cm和12 cm,则斜边上的高为___________cm.
12.如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子 BC 的长为17米,几分钟后船到达点 D的位置,此时绳子CD的长为 10米,问船向岸边移动了__________米.
13.四个全等的直角三角形的直角边分别为 a,b,斜边为 c.现把它们适当拼合,可以得到如图的图形.利用这个图形可以验证勾股定理,你能说明其中的道理吗 请试一试.
核心拓展
14.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪灵感.他惊喜地发现:当两个全等的直角三角形如图1或图 2 摆放时,都可以用“面积法”来证明.下面是小聪利用图 1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a +b =c .
证明:连接 DB,过点 D作 BC 边上的高DF,DF=EC=b-a.
因为
且
所以
所以a +b =c .
请参照上述证法,利用图 2 完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a +b =c .
证明:连接___________________________.
因为_______________________________________________________,
且 ________________________________________________________,
所以___________________________________________________________________.
所以a +b =c .
参考答案
1. D【解析】选项A 可以利用面积的关系式 a) =c 来验证勾股定理;选项 B可以利用面积的关系式 来验证勾股定理;选项C可以利用
面积的关系式 来验证勾股定理;选项 D无法验证勾股定理.
2.解:因为图1与图 2 拼出的大正方形面积相等,所以两个大正方形中空白部分的面积相等,所以c =b +a ,即a +b =c .
3. D【解析】由勾股定理,得AB=25,因此,少走的路程为24+7-25=6(米).
4.150 【解析】AC=150-60=90(mm),BC=180-60=120(mm),根据勾股定理,得AB =AC +BC =90 +120 =150 .所以AB=150mm.
5. C【解析】由题意可知:BE=CD=1.5m ,AE=AB-BE=4.5-1.5=3(m),CE=4m,
由勾股定理,得AC=5m .故选C.
6. C【解析】由于已知条件中△ABC 形状未确定,故分两种情况讨论.
当△ABC为锐角三角形时(如图1),即高AD在△ABC 内部,在 Rt△ABD中,AD =AB -BD ,即12 =15 -BD ,BD =81,所以BD=9,在Rt△ACD中,CD =AC -AD =13 -12 =25.所以CD=5.所以BC=9+5=14.△ABC的周长=15+13+14=42;当△ABC为钝角三角形时(如图2),即高AD在△ABC外部,此时BC=BD-CD=9-5=4,所以△ABC周长=15+13+4=32.
7. D【解析】设直角三角形斜边长为c,根据勾股定理,得a +b =c =25.因为 ab=8,所以(a-b) =a +b -2ab=25-2×8=9,即a-b=3,即小正方形的边长为3.
8. B 【解析】根据题意,得∠ECF=∠ACE+∠ACF= 所以△EFC为直角三角形.因为EF∥BC,CE平分∠ACB,CF平分∠ACD,所以∠ECB=∠MEC=∠ECM,∠DCF=∠CFM=∠MCF.所以EM=CM=MF=5,所以EF=10.在Rt△EFC中,由勾股定理,得CE +CF =EF =100.
9.35 【解析】由勾股定理可得直角三角形的斜边长为5m,所以所需长方形塑料薄膜的面积是5×7=35(m ).
10.5 【解析】如图,由题意,得AH=DE=1.
因为AB=BE,BH⊥AE,所以AE=2AH=2.
所以正方形ABCD的面积=AD =5.
11. 【解析】因为直角三角形的两直角边长分别为5cm 和12cm,所以斜边长的平方=5 +12 =13 .所以斜边=13cm.设斜边上的高为xcm,则 解得 即斜边上的高为
12.9 【解析】在 Rt△ABC中,
因为∠CAB=90°,BC=17米,AC=8米,所以AB =BC -AC =17 -8 =225.
所以AB=15米.同理可求AD=6米.所以BD=AB-AD=15-6=9(米),即船向岸边移动了9米.
13.解:图形的总面积可以表示为
也可以表示为 所以c +ab=a +b +ab.即a +b =c .
14.解:依次填写:
BD,过点 B作DE边上的高BF,则BF=b-a
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
