3.2 一定是直角三角形吗同步练习(含解析)
文档属性
| 名称 | 3.2 一定是直角三角形吗同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 22:43:10 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第三章 勾股定理
2 一定是直角三角形吗
基础夯实
知识点一 勾股定理的逆定理
1.满足下列条件的三角形中,不是直角三角形的是( )
A.三内角之比为1:2:3 B.三边长的平方之比9:25:16
C.三边长之比为3:4:5 D.三内角之比为3:4:5
2.如图,小红家的木门左下角有一点受潮,她想检测门是否变形,准备采用如下方法:先测量门的边 AB 和BC 的长,再测量点A 和点C间的距离,由此可推断∠B是否为直角,这样做的依据是( )
A.勾股定理
B.勾股定理的逆定理
C.三角形内角和定理
D.直角三角形的两锐角互余
3.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何 ”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大 题中的“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A.7.5 平方千米 B.15 平方千米 C.75 平方千米 D.750平方千米
4.古埃及人曾用“拉绳”的方法画直角,现有一根长24 cm的绳子,请你利用它拉出一个周长为24 cm的直角三角形,那么你拉出的直角三角形三边的长度分别为_________cm,_____________cm,_____________cm.
5.已知:在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,请根据下列a,b,c的长度,判断该三角形是否是直角三角形 并指出哪一个角是直角
(1)a=9,b=41,c=40;
(2)a=5k,b=12k,c=13k(k>0).
知识点二 勾股数
6.在下列四组数中,不是勾股数的一组数是( )
A. a=15,b=8,c=17 B. a=6,b=8,c=10
C. a=3,b=4,c=5 D. a=3,b=5,c=7
7.请完成以下未完成的勾股数:
(1)8,15,________; (2)10,26,__________.
易错点 忽视勾股数是正整数这一条件
8.下列各组数为勾股数的是____________(填序号).
①6,8,10; ②7,8,10; ③
能力提升
9.如图,在单位正方形组成的网格图中标有AB,CD,EF,GH 四条线段,其中能构成一个直角三角形三边的线段是( )
A. CD,EF,GH B. AB,EF,GH C. AB,CD,GH D. EF,AB,CD
10.适合下列条件的△ABC中,直角三角形有( )
(2)a=6,∠A=45°; (3)∠A=32°,∠B=58°;
(4)a=7,b=24,c=25; (5)a=2.5,b=2,c=3.
A.2个 B.3个 C.4个 D.5个
11.下列长度的三条线段能组成钝角三角形的是( )
A.3,4,4 B.3,4,5 C.3,4,6 D.3,4,7
12.三角形的三边长分别为 6,8,10,它的最短边上的高为____________.
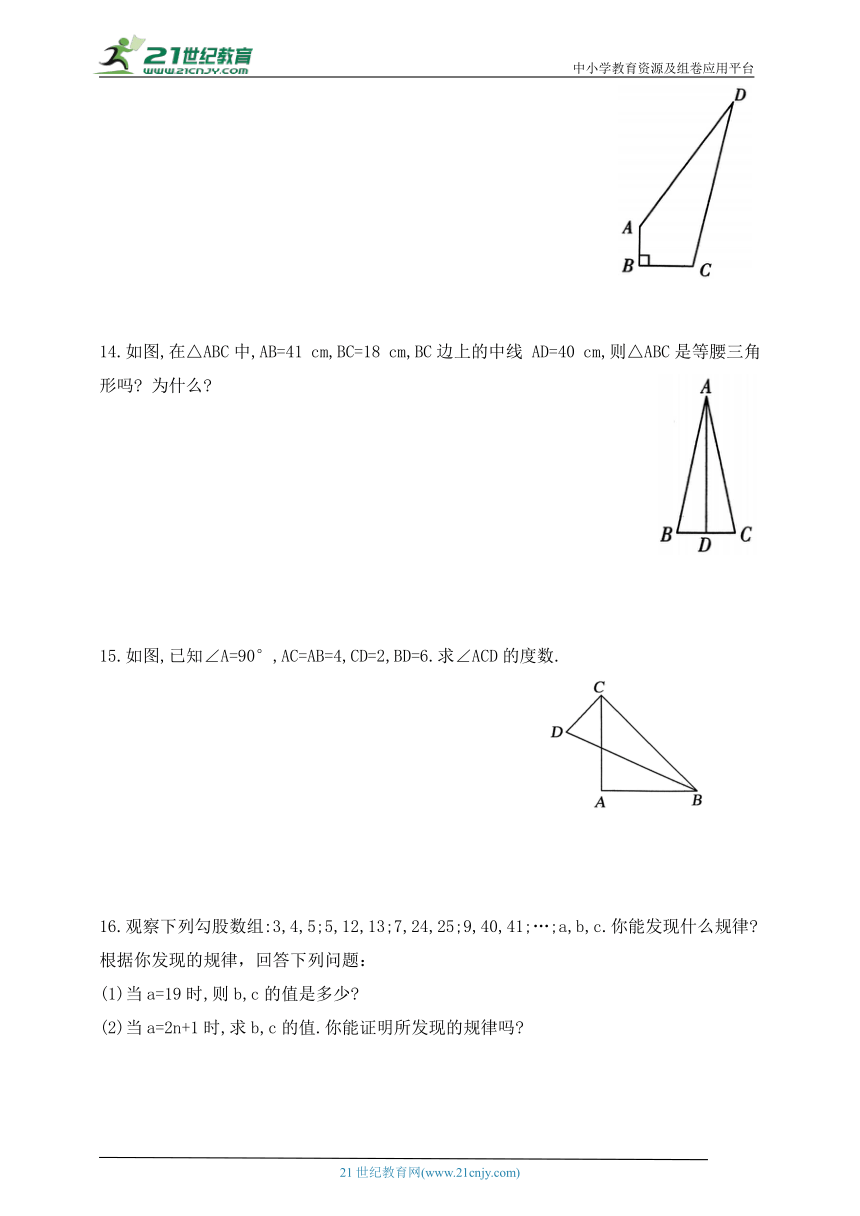
13.某经济开发区有一块四边形的空地ABCD,如图,现计划在空地上种植草皮,经测量,
∠B=90°,AB= 3 m,BC=4 m,AD=12 m,CD=13 m.若每种植1平方米草皮需要100元,问总共需要投入多少元
14.如图,在△ABC中,AB=41 cm,BC=18 cm,BC边上的中线 AD=40 cm,则△ABC是等腰三角形吗 为什么
15.如图,已知∠A=90°,AC=AB=4,CD=2,BD=6.求∠ACD的度数.
16.观察下列勾股数组:3,4,5;5,12,13;7,24,25;9,40,41;…;a,b,c.你能发现什么规律
根据你发现的规律,回答下列问题:
(1)当a=19时,则b,c的值是多少
(2)当a=2n+1时,求b,c的值.你能证明所发现的规律吗
核心拓展
17.刘老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 …
a 2 -1 3 -1 4 -1 5 -1 …
b 4 6 8 10 …
c 2 +1 3 +1 4 +1 5 +1 …
(1)请你分别观察a,b,c与n之间的关系,并用含自然数 n(n>1)的代数式表示.
a=_____________,b=______________,c=_____________.
(2)猜想:以a,b,c为边的三角形是否为直角三角形 并证明你的猜想.
参考答案
1. D【解析】当三内角之比为3:4:5 时,显然最大角小于另外两角之和,即不为90°,则不是直角三角形.
2. B【解析】因为AB +BC =AC ,所以△ABC是直角三角形,且∠B=90°.故选 B.
3. A 【解析】因为三角形沙田的三条边长分别为5里,12里,13里,5 +12 =13 ,
所以这个三角形沙田的形状为直角三角形,两直角边长分别为5里,12里.
又因为5里=5×500米=2 500米=2.5千米,12里=12×500米=6 000 米=6千米,
所以这个三角形沙田的面积 (平方千米).故选 A.
4.6 8 10
5.解:(1)是直角三角形,∠B是直角.
(2)是直角三角形,∠C 是直角.
6. D【解析】A.因为8 +15 =17 ,所以8,15,17是勾股数.B.因为6 +8 =10 ,所以6,8,10是勾股数.C.因为3 +4 =5 ,所以3,4,5 是勾股数.D. 因为3 +5 ≠7 ,所以3,5,7不是勾股数.故选 D.
7.(1)17 (2)2
8.①【解析】本题易忽视勾股数是正整数而填①③.
9. B【解析】设每个小正方形的边长为1,
则因为CD =2 +4 =20,AB =2 +2 =8,EF =1 +2 =5,GH =2 +3 =13,
所以AB +EF =GH .所以AB,EF,GH 这三条线段能构成一个直角三角形.
10. A 【解析】(1)因为两较小数的平方不等于最大数的平方,即 所以不是直角三角形;
(2)只知一边一角,三角形不确定,不是直角三角形;
(3)因为∠A+∠B=90°,所以是直角三角形;
(4)因为7 +24 =25 ,所以是直角三角形;
(5)因为2.5 +2 ≠3 ,所以不是直角三角形.
综上(3)(4)正确.故选 A.
11. C【解析】首先排除 D选项,因为3+4=7,不能构成三角形;然后再用勾股定理判断,排除 B选项,因为3和4的平方和等于5的平方,这是直角三角形;再观察A选项,最长边4小于5,肯定是锐角三角形;而选项C中,最长边为6大于5,一定是钝角三角形.
12.8 【解析】因为6 +8 =100=10 ,所以该三角形是直角三角形,直角边长为6与8,则最短边长为6,最短边上的高为8.
13.解:如图,连接AC,在 Rt△ABC中,由勾股定理,得AC =AB +BC =9+16=25.所以AC=5.
因为5 +12 =13 ,1即AC +AD =CD ,所以△ADC是直角三角形,
所以
所以总共需要投入36×100=3 600(元),
14.解:△ABC是等腰三角形,理由如下:
因为 BC=18 cm,BC边上的中线为AD,所以BD=CD=9 cm.
因为AB=41 cm,BD=9 cm,AD=40 cm,所以AB =1 681,BD +AD =1681.所以AB =BD +AD .
所以AD⊥BC.
又因为 BD=CD,所以AC=AB.所以△ABC是等腰三角形.
15.解:因为∠A=90°,AC=AB=4,所以∠ACB=∠ABC=45°.
在 Rt△ABC中,因为AC=AB=4,所以BC =AC +AB =32.又因为 CD=2,BD=6,
所以CD +BC =4+32=36,BD =36.所以CD +BC =BD .所以∠BCD=90°.
所以∠ACD=∠BCD-∠ACB=45°.
16.解:(1)当a=19时,设b=k,则c=k+1.
观察有如下规律:19 +k =(k+1) ,解得k=180.
故当a=19时,b=180,c=181.
(2)当a=2n+1时,设b=k,则c=k+1,
根据勾股定理a +b =c ,得(2n+1) +k =(k+1) ,解得k=2n(n+1).
即b=2n(n+1),c=2n(n+1)+1.证明如下:
a +b =(2n+1) +[2n(n+1)] =4n +8n +8n +4n+1,
c =[2n(n+1)+1] =4n +8n +8n +4n+1,
所以a +b =c .
所以以a,b,c为边组成的三角形是直角三角形.
17.解:(1)n -1 2n n +1
(2)猜想:以a,b,c为边的三角形是直角三角形.证明如下:
因为a=n -1,b=2n,c=n +1,
所以a +b =(n -1) +(2n) =n -2n +1+4n =n +2n +1=(n +1) .
因为c =(n +1) ,所以a +b =c .
所以以a,b,c为边的三角形是直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 勾股定理
2 一定是直角三角形吗
基础夯实
知识点一 勾股定理的逆定理
1.满足下列条件的三角形中,不是直角三角形的是( )
A.三内角之比为1:2:3 B.三边长的平方之比9:25:16
C.三边长之比为3:4:5 D.三内角之比为3:4:5
2.如图,小红家的木门左下角有一点受潮,她想检测门是否变形,准备采用如下方法:先测量门的边 AB 和BC 的长,再测量点A 和点C间的距离,由此可推断∠B是否为直角,这样做的依据是( )
A.勾股定理
B.勾股定理的逆定理
C.三角形内角和定理
D.直角三角形的两锐角互余
3.我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何 ”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大 题中的“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A.7.5 平方千米 B.15 平方千米 C.75 平方千米 D.750平方千米
4.古埃及人曾用“拉绳”的方法画直角,现有一根长24 cm的绳子,请你利用它拉出一个周长为24 cm的直角三角形,那么你拉出的直角三角形三边的长度分别为_________cm,_____________cm,_____________cm.
5.已知:在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,请根据下列a,b,c的长度,判断该三角形是否是直角三角形 并指出哪一个角是直角
(1)a=9,b=41,c=40;
(2)a=5k,b=12k,c=13k(k>0).
知识点二 勾股数
6.在下列四组数中,不是勾股数的一组数是( )
A. a=15,b=8,c=17 B. a=6,b=8,c=10
C. a=3,b=4,c=5 D. a=3,b=5,c=7
7.请完成以下未完成的勾股数:
(1)8,15,________; (2)10,26,__________.
易错点 忽视勾股数是正整数这一条件
8.下列各组数为勾股数的是____________(填序号).
①6,8,10; ②7,8,10; ③
能力提升
9.如图,在单位正方形组成的网格图中标有AB,CD,EF,GH 四条线段,其中能构成一个直角三角形三边的线段是( )
A. CD,EF,GH B. AB,EF,GH C. AB,CD,GH D. EF,AB,CD
10.适合下列条件的△ABC中,直角三角形有( )
(2)a=6,∠A=45°; (3)∠A=32°,∠B=58°;
(4)a=7,b=24,c=25; (5)a=2.5,b=2,c=3.
A.2个 B.3个 C.4个 D.5个
11.下列长度的三条线段能组成钝角三角形的是( )
A.3,4,4 B.3,4,5 C.3,4,6 D.3,4,7
12.三角形的三边长分别为 6,8,10,它的最短边上的高为____________.
13.某经济开发区有一块四边形的空地ABCD,如图,现计划在空地上种植草皮,经测量,
∠B=90°,AB= 3 m,BC=4 m,AD=12 m,CD=13 m.若每种植1平方米草皮需要100元,问总共需要投入多少元
14.如图,在△ABC中,AB=41 cm,BC=18 cm,BC边上的中线 AD=40 cm,则△ABC是等腰三角形吗 为什么
15.如图,已知∠A=90°,AC=AB=4,CD=2,BD=6.求∠ACD的度数.
16.观察下列勾股数组:3,4,5;5,12,13;7,24,25;9,40,41;…;a,b,c.你能发现什么规律
根据你发现的规律,回答下列问题:
(1)当a=19时,则b,c的值是多少
(2)当a=2n+1时,求b,c的值.你能证明所发现的规律吗
核心拓展
17.刘老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 …
a 2 -1 3 -1 4 -1 5 -1 …
b 4 6 8 10 …
c 2 +1 3 +1 4 +1 5 +1 …
(1)请你分别观察a,b,c与n之间的关系,并用含自然数 n(n>1)的代数式表示.
a=_____________,b=______________,c=_____________.
(2)猜想:以a,b,c为边的三角形是否为直角三角形 并证明你的猜想.
参考答案
1. D【解析】当三内角之比为3:4:5 时,显然最大角小于另外两角之和,即不为90°,则不是直角三角形.
2. B【解析】因为AB +BC =AC ,所以△ABC是直角三角形,且∠B=90°.故选 B.
3. A 【解析】因为三角形沙田的三条边长分别为5里,12里,13里,5 +12 =13 ,
所以这个三角形沙田的形状为直角三角形,两直角边长分别为5里,12里.
又因为5里=5×500米=2 500米=2.5千米,12里=12×500米=6 000 米=6千米,
所以这个三角形沙田的面积 (平方千米).故选 A.
4.6 8 10
5.解:(1)是直角三角形,∠B是直角.
(2)是直角三角形,∠C 是直角.
6. D【解析】A.因为8 +15 =17 ,所以8,15,17是勾股数.B.因为6 +8 =10 ,所以6,8,10是勾股数.C.因为3 +4 =5 ,所以3,4,5 是勾股数.D. 因为3 +5 ≠7 ,所以3,5,7不是勾股数.故选 D.
7.(1)17 (2)2
8.①【解析】本题易忽视勾股数是正整数而填①③.
9. B【解析】设每个小正方形的边长为1,
则因为CD =2 +4 =20,AB =2 +2 =8,EF =1 +2 =5,GH =2 +3 =13,
所以AB +EF =GH .所以AB,EF,GH 这三条线段能构成一个直角三角形.
10. A 【解析】(1)因为两较小数的平方不等于最大数的平方,即 所以不是直角三角形;
(2)只知一边一角,三角形不确定,不是直角三角形;
(3)因为∠A+∠B=90°,所以是直角三角形;
(4)因为7 +24 =25 ,所以是直角三角形;
(5)因为2.5 +2 ≠3 ,所以不是直角三角形.
综上(3)(4)正确.故选 A.
11. C【解析】首先排除 D选项,因为3+4=7,不能构成三角形;然后再用勾股定理判断,排除 B选项,因为3和4的平方和等于5的平方,这是直角三角形;再观察A选项,最长边4小于5,肯定是锐角三角形;而选项C中,最长边为6大于5,一定是钝角三角形.
12.8 【解析】因为6 +8 =100=10 ,所以该三角形是直角三角形,直角边长为6与8,则最短边长为6,最短边上的高为8.
13.解:如图,连接AC,在 Rt△ABC中,由勾股定理,得AC =AB +BC =9+16=25.所以AC=5.
因为5 +12 =13 ,1即AC +AD =CD ,所以△ADC是直角三角形,
所以
所以总共需要投入36×100=3 600(元),
14.解:△ABC是等腰三角形,理由如下:
因为 BC=18 cm,BC边上的中线为AD,所以BD=CD=9 cm.
因为AB=41 cm,BD=9 cm,AD=40 cm,所以AB =1 681,BD +AD =1681.所以AB =BD +AD .
所以AD⊥BC.
又因为 BD=CD,所以AC=AB.所以△ABC是等腰三角形.
15.解:因为∠A=90°,AC=AB=4,所以∠ACB=∠ABC=45°.
在 Rt△ABC中,因为AC=AB=4,所以BC =AC +AB =32.又因为 CD=2,BD=6,
所以CD +BC =4+32=36,BD =36.所以CD +BC =BD .所以∠BCD=90°.
所以∠ACD=∠BCD-∠ACB=45°.
16.解:(1)当a=19时,设b=k,则c=k+1.
观察有如下规律:19 +k =(k+1) ,解得k=180.
故当a=19时,b=180,c=181.
(2)当a=2n+1时,设b=k,则c=k+1,
根据勾股定理a +b =c ,得(2n+1) +k =(k+1) ,解得k=2n(n+1).
即b=2n(n+1),c=2n(n+1)+1.证明如下:
a +b =(2n+1) +[2n(n+1)] =4n +8n +8n +4n+1,
c =[2n(n+1)+1] =4n +8n +8n +4n+1,
所以a +b =c .
所以以a,b,c为边组成的三角形是直角三角形.
17.解:(1)n -1 2n n +1
(2)猜想:以a,b,c为边的三角形是直角三角形.证明如下:
因为a=n -1,b=2n,c=n +1,
所以a +b =(n -1) +(2n) =n -2n +1+4n =n +2n +1=(n +1) .
因为c =(n +1) ,所以a +b =c .
所以以a,b,c为边的三角形是直角三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
