第三章 勾股定理章末复习题(含解析)
图片预览
文档简介
中小学教育资源及组卷应用平台
第三章 勾股定理
章末复习
考点整合
考点1 勾股定理及验证
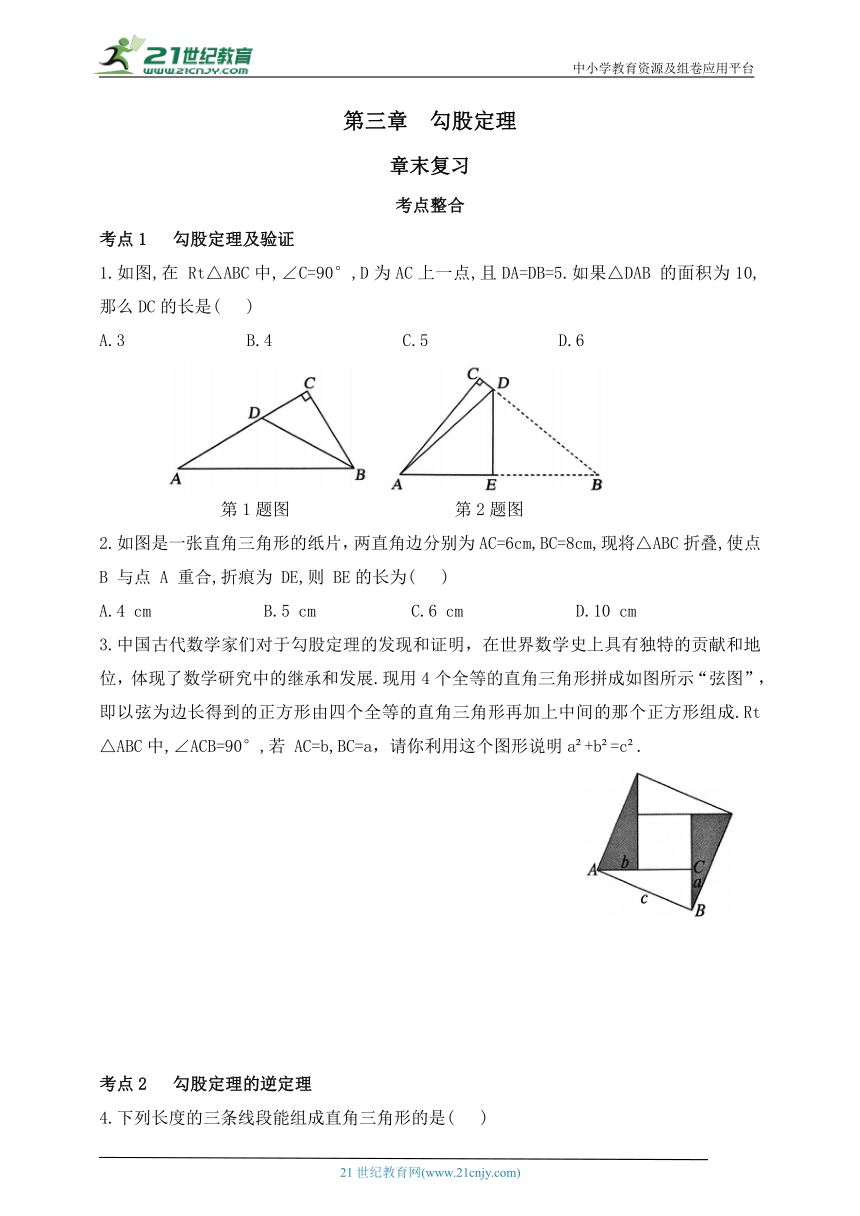
1.如图,在 Rt△ABC中,∠C=90°,D为AC上一点,且DA=DB=5.如果△DAB 的面积为10,那么DC的长是( )
A.3 B.4 C.5 D.6
第1题图 第2题图
2.如图是一张直角三角形的纸片,两直角边分别为AC=6cm,BC=8cm,现将△ABC折叠,使点 B 与点 A 重合,折痕为 DE,则 BE的长为( )
A.4 cm B.5 cm C.6 cm D.10 cm
3.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”,即以弦为边长得到的正方形由四个全等的直角三角形再加上中间的那个正方形组成.Rt△ABC中,∠ACB=90°,若 AC=b,BC=a,请你利用这个图形说明a +b =c .
考点2 勾股定理的逆定理
4.下列长度的三条线段能组成直角三角形的是( )
A.3,4,5 B.2,3,4 C.4,6,7 D.5,11,12
5.下列说法中,错误的是( )
A.在△ABC中,∠C=∠A-∠B,则△ABC为直角三角形
B.在△ABC中,若∠A:∠B:∠C=5:2:3,则△ABC为直角三角形
C.在△ABC中,若 则△ABC为直角三角形
D.在△ABC中,若a:b:c=3:2:4,则△ABC为直角三角形
考点3 勾股定理的应用
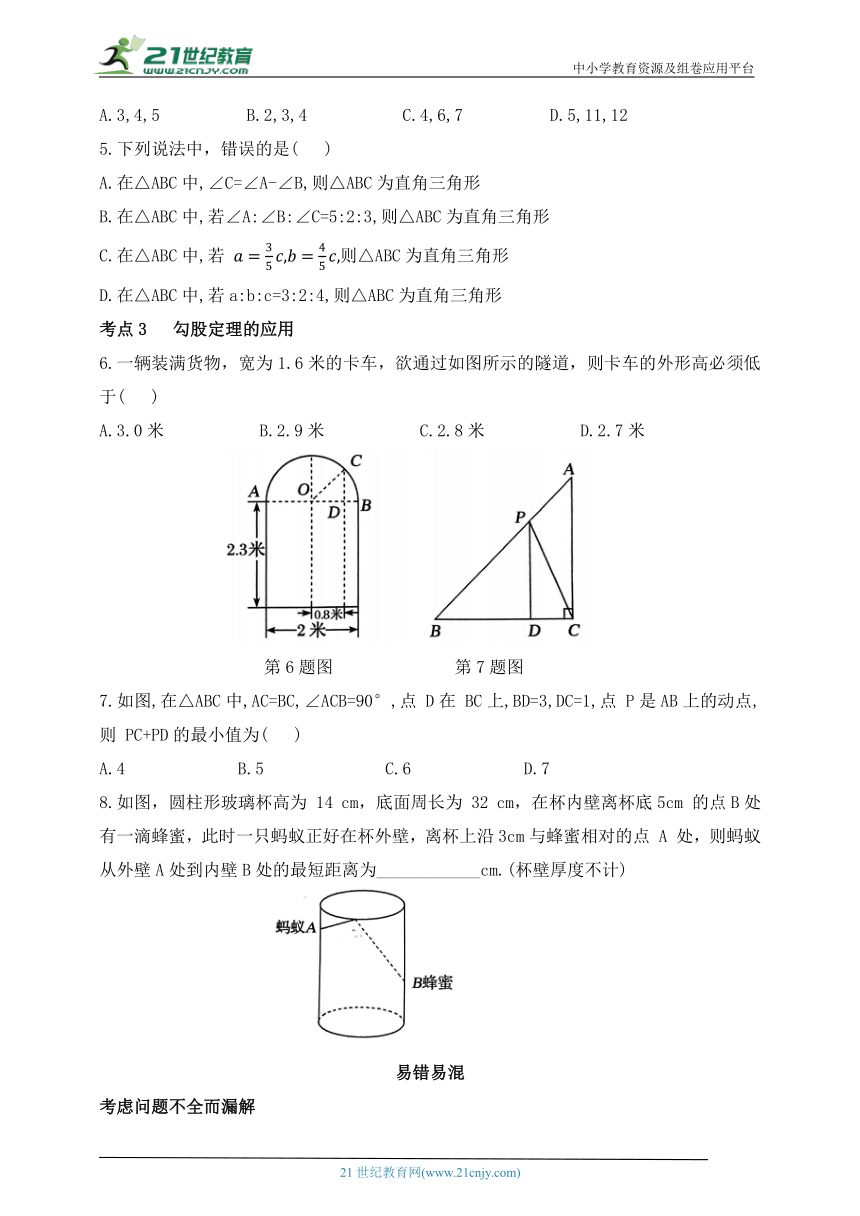
6.一辆装满货物,宽为1.6米的卡车,欲通过如图所示的隧道,则卡车的外形高必须低于( )
A.3.0米 B.2.9米 C.2.8米 D.2.7米
第6题图 第7题图
7.如图,在△ABC中,AC=BC,∠ACB=90°,点 D在 BC上,BD=3,DC=1,点 P是AB上的动点,则 PC+PD的最小值为( )
A.4 B.5 C.6 D.7
8.如图,圆柱形玻璃杯高为 14 cm,底面周长为 32 cm,在杯内壁离杯底5cm 的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点 A 处,则蚂蚁从外壁A处到内壁B处的最短距离为____________cm.(杯壁厚度不计)
易错易混
考虑问题不全而漏解
9.已知一个直角三角形的两边长分别为6和8,则第三边长的平方是__________.
培优创新
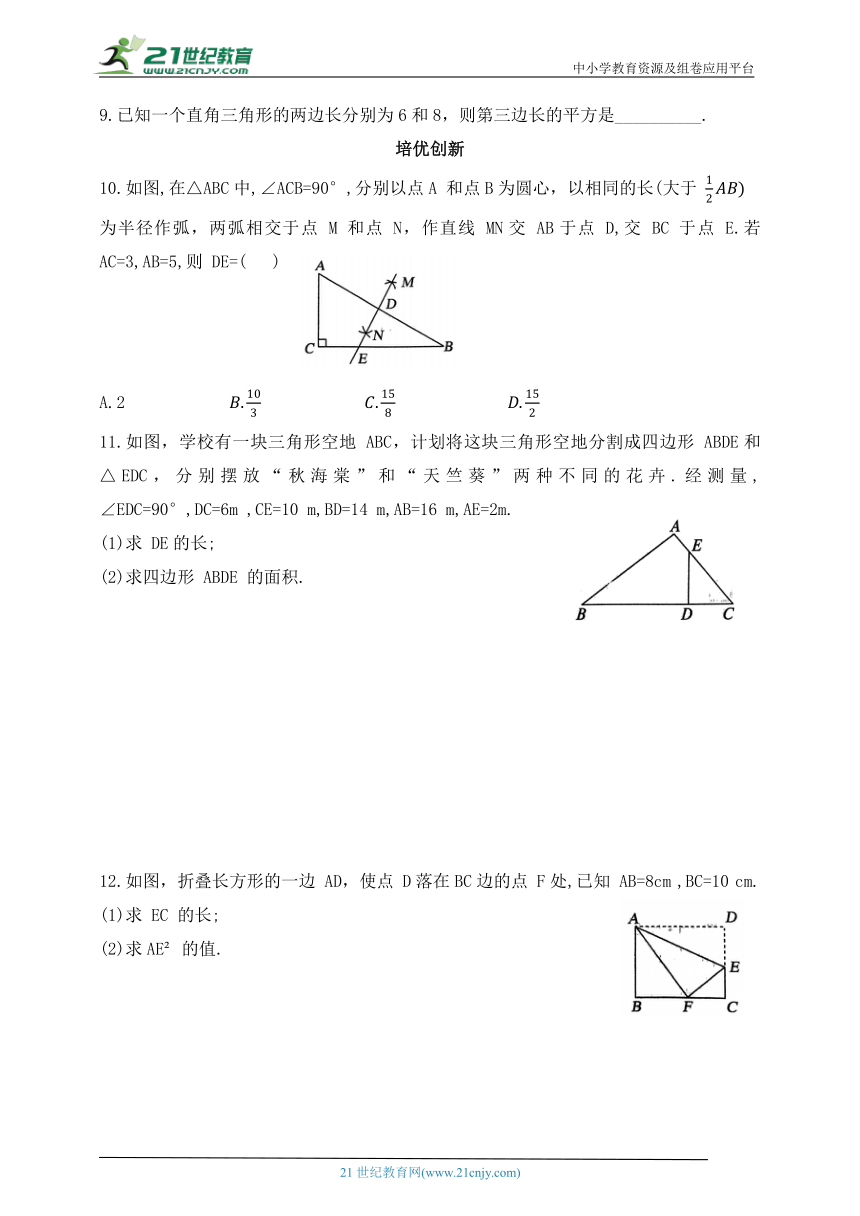
10.如图,在△ABC中,∠ACB=90°,分别以点A 和点B为圆心,以相同的长(大于
为半径作弧,两弧相交于点 M 和点 N,作直线 MN交 AB于点 D,交 BC 于点 E.若AC=3,AB=5,则 DE=( )
A.2
11.如图,学校有一块三角形空地 ABC,计划将这块三角形空地分割成四边形 ABDE和 △EDC,分别摆放“秋海棠”和“天竺葵”两种不同的花卉.经测量, ∠EDC=90°,DC=6m ,CE=10 m,BD=14 m,AB=16 m,AE=2m.
(1)求 DE的长;
(2)求四边形 ABDE 的面积.
12.如图,折叠长方形的一边 AD,使点 D落在BC边的点 F处,已知 AB=8cm ,BC=10 cm.
(1)求 EC 的长;
(2)求AE 的值.
参考答案
1. A 2. B
3.解:因为大正方形面积为c ,直角三角形面积为 小正方形面积为(b-a) ,
所以 即a +b =c .
4. A 5. D 6. B
7. B【解析】如图,过点C作CO⊥AB于点O,延长CO到点C',使OC,连接 DC',交 AB于点P,连接CP.此时DP+CP=DC'的值最小.
因为BD=3,DC=1,所以BC=4.连接BC',由对称性可知∠C'BA=∠CBA=45°,所以 所以 所以 根据勾股定理,得 所以
8.20【解析】如图,将杯子侧面展开,作A关于EF 的对称点A',连接A'B,则 A'B即为最短距离, 16 +12 =20 ,所以
9.100 或28 10. C
11.解:(1)在 Rt△EDC中,∠EDC=90°,DC=6 m,CE=10m,所以DE =EC -CD =10 -6 =64,所以DE=8m,即DE的长为 8 m.
(2)如图,连接BE.
在 Rt△EBD中,BD=14 m,ED=8m,所以BE =BD +ED =14 +8 =260.
因为AB=16 m,AE=2m,所以AB +AE =16 +2 =260.所以AB +AE =BE .
所以△ABE是直角三角形,∠A=90°.所以
又因为 所以四边形 ABDE 的面积 =72(m ).
12.解:(1)因为四边形 ABCD为长方形,所以AD=BC=10 cm,DC=AB=8cm .
由折叠可得△ADE≌△AFE,所以AF=AD=10 cm,EF=ED.
设EF=ED=xcm,则 EC=(8-x) cm.
在Rt△ABF中,由勾股定理,得 所以FC=BC-BF=10-6=4(cm).
在 Rt△EFC中,由勾股定理,得EF =CF +EC ,即x =4 +(8-x) .解得x=5,8-x=3.
所以 EC 的长为 3c m.
(2)在 Rt△ADE中,由勾股定理,得AE =AD +DE =10 +5 =125.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 勾股定理
章末复习
考点整合
考点1 勾股定理及验证
1.如图,在 Rt△ABC中,∠C=90°,D为AC上一点,且DA=DB=5.如果△DAB 的面积为10,那么DC的长是( )
A.3 B.4 C.5 D.6
第1题图 第2题图
2.如图是一张直角三角形的纸片,两直角边分别为AC=6cm,BC=8cm,现将△ABC折叠,使点 B 与点 A 重合,折痕为 DE,则 BE的长为( )
A.4 cm B.5 cm C.6 cm D.10 cm
3.中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”,即以弦为边长得到的正方形由四个全等的直角三角形再加上中间的那个正方形组成.Rt△ABC中,∠ACB=90°,若 AC=b,BC=a,请你利用这个图形说明a +b =c .
考点2 勾股定理的逆定理
4.下列长度的三条线段能组成直角三角形的是( )
A.3,4,5 B.2,3,4 C.4,6,7 D.5,11,12
5.下列说法中,错误的是( )
A.在△ABC中,∠C=∠A-∠B,则△ABC为直角三角形
B.在△ABC中,若∠A:∠B:∠C=5:2:3,则△ABC为直角三角形
C.在△ABC中,若 则△ABC为直角三角形
D.在△ABC中,若a:b:c=3:2:4,则△ABC为直角三角形
考点3 勾股定理的应用
6.一辆装满货物,宽为1.6米的卡车,欲通过如图所示的隧道,则卡车的外形高必须低于( )
A.3.0米 B.2.9米 C.2.8米 D.2.7米
第6题图 第7题图
7.如图,在△ABC中,AC=BC,∠ACB=90°,点 D在 BC上,BD=3,DC=1,点 P是AB上的动点,则 PC+PD的最小值为( )
A.4 B.5 C.6 D.7
8.如图,圆柱形玻璃杯高为 14 cm,底面周长为 32 cm,在杯内壁离杯底5cm 的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点 A 处,则蚂蚁从外壁A处到内壁B处的最短距离为____________cm.(杯壁厚度不计)
易错易混
考虑问题不全而漏解
9.已知一个直角三角形的两边长分别为6和8,则第三边长的平方是__________.
培优创新
10.如图,在△ABC中,∠ACB=90°,分别以点A 和点B为圆心,以相同的长(大于
为半径作弧,两弧相交于点 M 和点 N,作直线 MN交 AB于点 D,交 BC 于点 E.若AC=3,AB=5,则 DE=( )
A.2
11.如图,学校有一块三角形空地 ABC,计划将这块三角形空地分割成四边形 ABDE和 △EDC,分别摆放“秋海棠”和“天竺葵”两种不同的花卉.经测量, ∠EDC=90°,DC=6m ,CE=10 m,BD=14 m,AB=16 m,AE=2m.
(1)求 DE的长;
(2)求四边形 ABDE 的面积.
12.如图,折叠长方形的一边 AD,使点 D落在BC边的点 F处,已知 AB=8cm ,BC=10 cm.
(1)求 EC 的长;
(2)求AE 的值.
参考答案
1. A 2. B
3.解:因为大正方形面积为c ,直角三角形面积为 小正方形面积为(b-a) ,
所以 即a +b =c .
4. A 5. D 6. B
7. B【解析】如图,过点C作CO⊥AB于点O,延长CO到点C',使OC,连接 DC',交 AB于点P,连接CP.此时DP+CP=DC'的值最小.
因为BD=3,DC=1,所以BC=4.连接BC',由对称性可知∠C'BA=∠CBA=45°,所以 所以 所以 根据勾股定理,得 所以
8.20【解析】如图,将杯子侧面展开,作A关于EF 的对称点A',连接A'B,则 A'B即为最短距离, 16 +12 =20 ,所以
9.100 或28 10. C
11.解:(1)在 Rt△EDC中,∠EDC=90°,DC=6 m,CE=10m,所以DE =EC -CD =10 -6 =64,所以DE=8m,即DE的长为 8 m.
(2)如图,连接BE.
在 Rt△EBD中,BD=14 m,ED=8m,所以BE =BD +ED =14 +8 =260.
因为AB=16 m,AE=2m,所以AB +AE =16 +2 =260.所以AB +AE =BE .
所以△ABE是直角三角形,∠A=90°.所以
又因为 所以四边形 ABDE 的面积 =72(m ).
12.解:(1)因为四边形 ABCD为长方形,所以AD=BC=10 cm,DC=AB=8cm .
由折叠可得△ADE≌△AFE,所以AF=AD=10 cm,EF=ED.
设EF=ED=xcm,则 EC=(8-x) cm.
在Rt△ABF中,由勾股定理,得 所以FC=BC-BF=10-6=4(cm).
在 Rt△EFC中,由勾股定理,得EF =CF +EC ,即x =4 +(8-x) .解得x=5,8-x=3.
所以 EC 的长为 3c m.
(2)在 Rt△ADE中,由勾股定理,得AE =AD +DE =10 +5 =125.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
