第三章 勾股定理培优专题 折叠问题中的勾股定理应用(含解析)
文档属性
| 名称 | 第三章 勾股定理培优专题 折叠问题中的勾股定理应用(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 22:51:42 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第三章 勾股定理
培优专题 折叠问题中的勾股定理应用
类型1 勾股定理在三角形折叠中的应用
1.如图,Rt△ABC 中,AB=9,BC=6,∠B=90°,将△ABC折叠,使点 A 与BC的中点 D重合,折痕为 MN,则线段 BN 的长为( )
C.4 D.5
第1题图 第2题图
2.如图,三角形纸片 ABC中,∠BAC=90°,AB=2,AC=3.沿过点 A 的直线将纸片折叠,使点 B落在边 BC上的点 D处;再折叠纸片,使点C与点 D重合,若折痕与 AC 的交点为E,则AE 的长是 ( )
3.小王剪了两张直角三角形纸片,进行了如下的操作:
操作一:如图 1,将 Rt△ABC沿某条直线折叠,使斜边的两个端点 A 与B 重合,折痕为DE.
(1)如果 AC=6 cm,AB=10 cm,可求得△ACD的周长为___________cm;
(2)如果∠CAD:∠BAD=1:4,可求得∠B 的度数为_____________;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边 AC沿直线AD折叠,使它落在斜边 AB上,且与AE重合,若AC=9cm,AB=15 cm,请求出CD的长.
类型2 勾股定理在四边形折叠中的应用
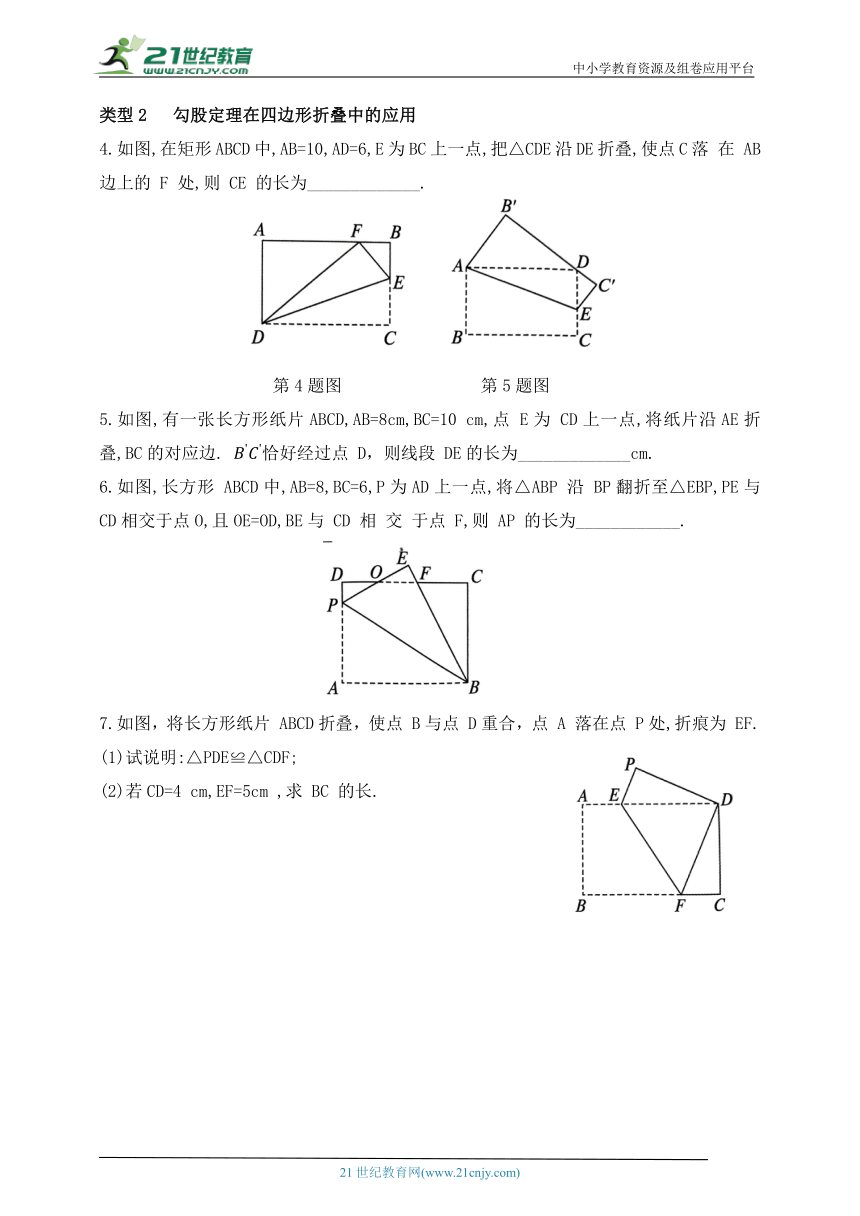
4.如图,在矩形ABCD中,AB=10,AD=6,E为BC上一点,把△CDE沿DE折叠,使点C落 在 AB边上的 F 处,则 CE 的长为_____________.
第4题图 第5题图
5.如图,有一张长方形纸片ABCD,AB=8cm,BC=10 cm,点 E为 CD上一点,将纸片沿AE折叠,BC的对应边. 恰好经过点 D,则线段 DE的长为_____________cm.
6.如图,长方形 ABCD中,AB=8,BC=6,P为AD上一点,将△ABP 沿 BP翻折至△EBP,PE与CD相交于点O,且OE=OD,BE与 CD 相 交 于点 F,则 AP 的长为____________.
7.如图,将长方形纸片 ABCD折叠,使点 B与点 D重合,点 A 落在点 P处,折痕为 EF.
(1)试说明:△PDE≌△CDF;
(2)若CD=4 cm,EF=5cm ,求 BC 的长.
参考答案
1. C 【解析】由折叠知 DN=AN=9-BN.因为点D为BC的中点,所以 因为∠B=90°,所以NB +DB =DN ,即BN +3 =(9-BN) ,解得BN=4.故选C.
2. A 【解析】因为沿过点A 的直线将纸片折叠,使点B落在边BC上的点D处,
所以AD=AB=2,∠B=∠ADB.
因为折叠纸片,使点C与点D重合,所以CE=DE,∠C=∠CDE.
因为∠BAC=90°,所以∠B+∠C=90°.所以∠ADB+∠CDE=90°.
所以∠ADE=90°.所以AD +DE =AE .
设AE=x,则CE=DE=3-x.
所以2 +(3-x) =x ,解得 所以 故选A.
3.解:操作一:
(1)14【解析】在 Rt△ABC 中,AC=6 cm,AB=10 cm,根据勾股定理,得 BC=8cm .
由折叠知AD=BD.所以△ACD的周长=AC+CD+AD=AC+CD+BD=AC+BC=6+8=14(cm).
(2)40°.
操作二:在 Rt△ABC中,AC=9 cm,AB=15 cm,根据勾股定理,得 BC =AB -AC =15 -9 =144.
所以BC=12 cm.由折叠知AE=AC=9 cm.
因为AB=15 cm,所以BE=AB-AE=6cm.
设CD=x cm,则 BD=(12-x) cm,DE=CD=x cm.
在 Rt△BDE中,根据勾股定理,得DE +BE =BD ,即x +6 =(12-x) .解得x=4.5.所以CD=4.5cm .
【解析】设 CE=x,则BE=6-x.
由折叠性质,知EF=CE=x,DF=CD=AB=10.
在Rt△DAF中,AD=6,DF=10,所以AF=8.所以BF=AB-AF=10-8=2.
在Rt△BEF中,BE +BF =EF ,即((6-x) +2 =x .解得
5.5 【解析】因为将纸片沿AE折叠,BC的对应边B'C'恰好经过点D,所以 C'E,所 所以
所以
因为 ,即DE =4 +(8-DE) ,所以DE=5cm .
6. 【解析】因为 OD=OE,∠D=∠E=90°,∠DOP=∠EOF,所以△DPO≌△EFO(ASA).
所以PO=FO,EF=DP.所以PE=DF.
设AP的长为x,则PE=DF=x,DP=EF=6-x,所以BF=BE-EF=8-(6-x)=2+x,CF=DC-DF=8-x.
在Rt△BCF中,.BF =BC +CF ,即(2+x) =6 +(8-x) .所以
7.解:(1)因为四边形ABCD是长方形,
所以∠A=∠ADC=∠B=∠C=90°,AB=CD.
由折叠得AB=PD,∠A=∠P=90°,∠B=∠PDF=90°,所以 PD=CD.
因为∠PDF=∠ADC=90°,所以∠PDE=∠CDF.
在△PDE和△CDF中,所以△PDE≌△CDF(ASA).
(2)如图,过点 E作EG⊥BC于点G,所以∠EGF=90°,EG=CD=4 cm.
在 Rt△EGF中,由勾股定理,得FG =EF -EG =5 -4 =9,所以 FG=3cm.
设CF=x cm,则 PE=AE=BG=x cm.
因为△PDE≌△CDF,所以DF=DE=CG=(x+3) cm.
在Rt△CDF中,由勾股定理,得DF =CD +CF ,即x +4 =(x+3) ,所以
所以 所以BC的长为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 勾股定理
培优专题 折叠问题中的勾股定理应用
类型1 勾股定理在三角形折叠中的应用
1.如图,Rt△ABC 中,AB=9,BC=6,∠B=90°,将△ABC折叠,使点 A 与BC的中点 D重合,折痕为 MN,则线段 BN 的长为( )
C.4 D.5
第1题图 第2题图
2.如图,三角形纸片 ABC中,∠BAC=90°,AB=2,AC=3.沿过点 A 的直线将纸片折叠,使点 B落在边 BC上的点 D处;再折叠纸片,使点C与点 D重合,若折痕与 AC 的交点为E,则AE 的长是 ( )
3.小王剪了两张直角三角形纸片,进行了如下的操作:
操作一:如图 1,将 Rt△ABC沿某条直线折叠,使斜边的两个端点 A 与B 重合,折痕为DE.
(1)如果 AC=6 cm,AB=10 cm,可求得△ACD的周长为___________cm;
(2)如果∠CAD:∠BAD=1:4,可求得∠B 的度数为_____________;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边 AC沿直线AD折叠,使它落在斜边 AB上,且与AE重合,若AC=9cm,AB=15 cm,请求出CD的长.
类型2 勾股定理在四边形折叠中的应用
4.如图,在矩形ABCD中,AB=10,AD=6,E为BC上一点,把△CDE沿DE折叠,使点C落 在 AB边上的 F 处,则 CE 的长为_____________.
第4题图 第5题图
5.如图,有一张长方形纸片ABCD,AB=8cm,BC=10 cm,点 E为 CD上一点,将纸片沿AE折叠,BC的对应边. 恰好经过点 D,则线段 DE的长为_____________cm.
6.如图,长方形 ABCD中,AB=8,BC=6,P为AD上一点,将△ABP 沿 BP翻折至△EBP,PE与CD相交于点O,且OE=OD,BE与 CD 相 交 于点 F,则 AP 的长为____________.
7.如图,将长方形纸片 ABCD折叠,使点 B与点 D重合,点 A 落在点 P处,折痕为 EF.
(1)试说明:△PDE≌△CDF;
(2)若CD=4 cm,EF=5cm ,求 BC 的长.
参考答案
1. C 【解析】由折叠知 DN=AN=9-BN.因为点D为BC的中点,所以 因为∠B=90°,所以NB +DB =DN ,即BN +3 =(9-BN) ,解得BN=4.故选C.
2. A 【解析】因为沿过点A 的直线将纸片折叠,使点B落在边BC上的点D处,
所以AD=AB=2,∠B=∠ADB.
因为折叠纸片,使点C与点D重合,所以CE=DE,∠C=∠CDE.
因为∠BAC=90°,所以∠B+∠C=90°.所以∠ADB+∠CDE=90°.
所以∠ADE=90°.所以AD +DE =AE .
设AE=x,则CE=DE=3-x.
所以2 +(3-x) =x ,解得 所以 故选A.
3.解:操作一:
(1)14【解析】在 Rt△ABC 中,AC=6 cm,AB=10 cm,根据勾股定理,得 BC=8cm .
由折叠知AD=BD.所以△ACD的周长=AC+CD+AD=AC+CD+BD=AC+BC=6+8=14(cm).
(2)40°.
操作二:在 Rt△ABC中,AC=9 cm,AB=15 cm,根据勾股定理,得 BC =AB -AC =15 -9 =144.
所以BC=12 cm.由折叠知AE=AC=9 cm.
因为AB=15 cm,所以BE=AB-AE=6cm.
设CD=x cm,则 BD=(12-x) cm,DE=CD=x cm.
在 Rt△BDE中,根据勾股定理,得DE +BE =BD ,即x +6 =(12-x) .解得x=4.5.所以CD=4.5cm .
【解析】设 CE=x,则BE=6-x.
由折叠性质,知EF=CE=x,DF=CD=AB=10.
在Rt△DAF中,AD=6,DF=10,所以AF=8.所以BF=AB-AF=10-8=2.
在Rt△BEF中,BE +BF =EF ,即((6-x) +2 =x .解得
5.5 【解析】因为将纸片沿AE折叠,BC的对应边B'C'恰好经过点D,所以 C'E,所 所以
所以
因为 ,即DE =4 +(8-DE) ,所以DE=5cm .
6. 【解析】因为 OD=OE,∠D=∠E=90°,∠DOP=∠EOF,所以△DPO≌△EFO(ASA).
所以PO=FO,EF=DP.所以PE=DF.
设AP的长为x,则PE=DF=x,DP=EF=6-x,所以BF=BE-EF=8-(6-x)=2+x,CF=DC-DF=8-x.
在Rt△BCF中,.BF =BC +CF ,即(2+x) =6 +(8-x) .所以
7.解:(1)因为四边形ABCD是长方形,
所以∠A=∠ADC=∠B=∠C=90°,AB=CD.
由折叠得AB=PD,∠A=∠P=90°,∠B=∠PDF=90°,所以 PD=CD.
因为∠PDF=∠ADC=90°,所以∠PDE=∠CDF.
在△PDE和△CDF中,所以△PDE≌△CDF(ASA).
(2)如图,过点 E作EG⊥BC于点G,所以∠EGF=90°,EG=CD=4 cm.
在 Rt△EGF中,由勾股定理,得FG =EF -EG =5 -4 =9,所以 FG=3cm.
设CF=x cm,则 PE=AE=BG=x cm.
因为△PDE≌△CDF,所以DF=DE=CG=(x+3) cm.
在Rt△CDF中,由勾股定理,得DF =CD +CF ,即x +4 =(x+3) ,所以
所以 所以BC的长为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
