第三章 勾股定理单元测试题(含解析)
图片预览
文档简介
中小学教育资源及组卷应用平台
第三章 勾股定理
单元测试卷
(时间:120分钟 分值:150分)
一、选择题(每小题 4分,共 40分)
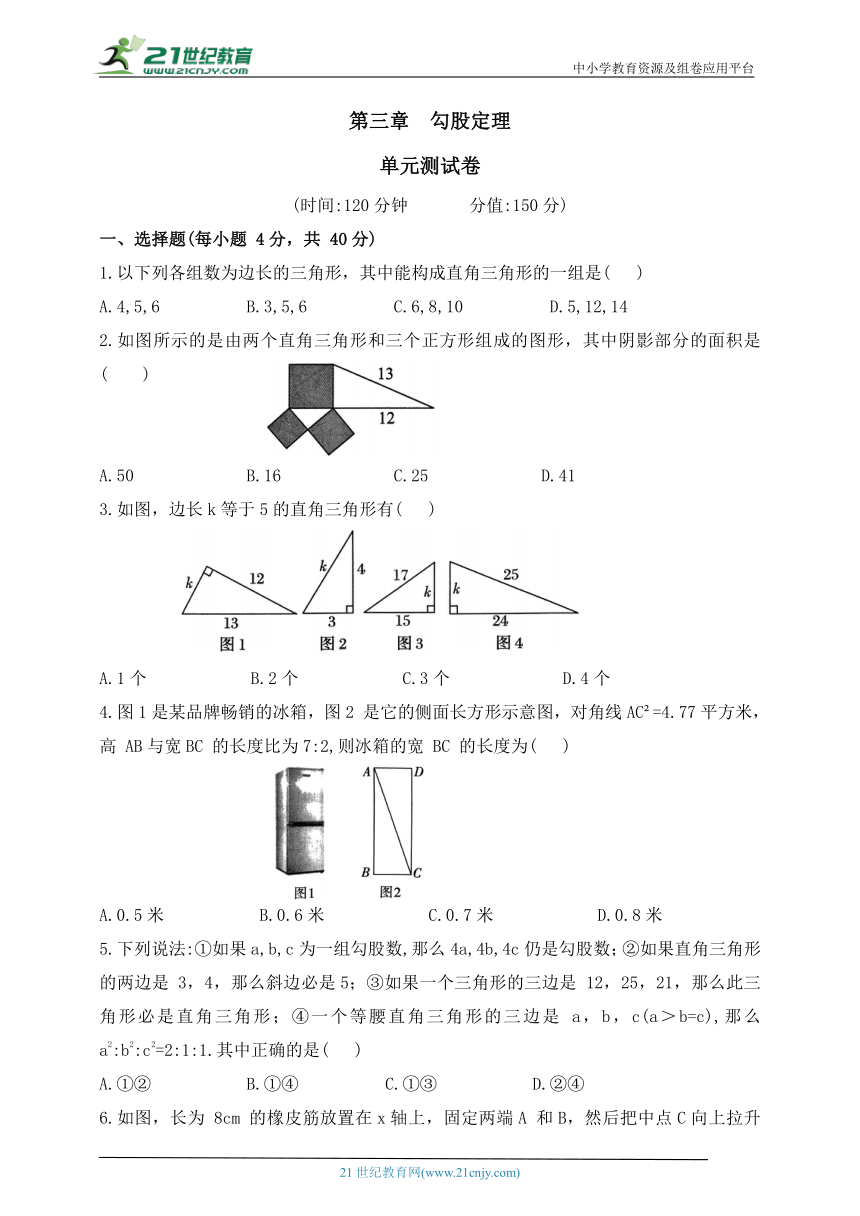
1.以下列各组数为边长的三角形,其中能构成直角三角形的一组是( )
A.4,5,6 B.3,5,6 C.6,8,10 D.5,12,14
2.如图所示的是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是( )
A.50 B.16 C.25 D.41
3.如图,边长k等于5的直角三角形有( )
A.1个 B.2个 C.3个 D.4个
4.图1是某品牌畅销的冰箱,图2 是它的侧面长方形示意图,对角线AC =4.77平方米,高 AB与宽BC 的长度比为7:2,则冰箱的宽 BC 的长度为( )
A.0.5米 B.0.6米 C.0.7米 D.0.8米
5.下列说法:①如果a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数;②如果直角三角形的两边是 3,4,那么斜边必是5;③如果一个三角形的三边是 12,25,21,那么此三角形必是直角三角形;④一个等腰直角三角形的三边是 a,b,c(a>b=c),那么a2:b2:c2=2:1:1.其中正确的是( )
A.①② B.①④ C.①③ D.②④
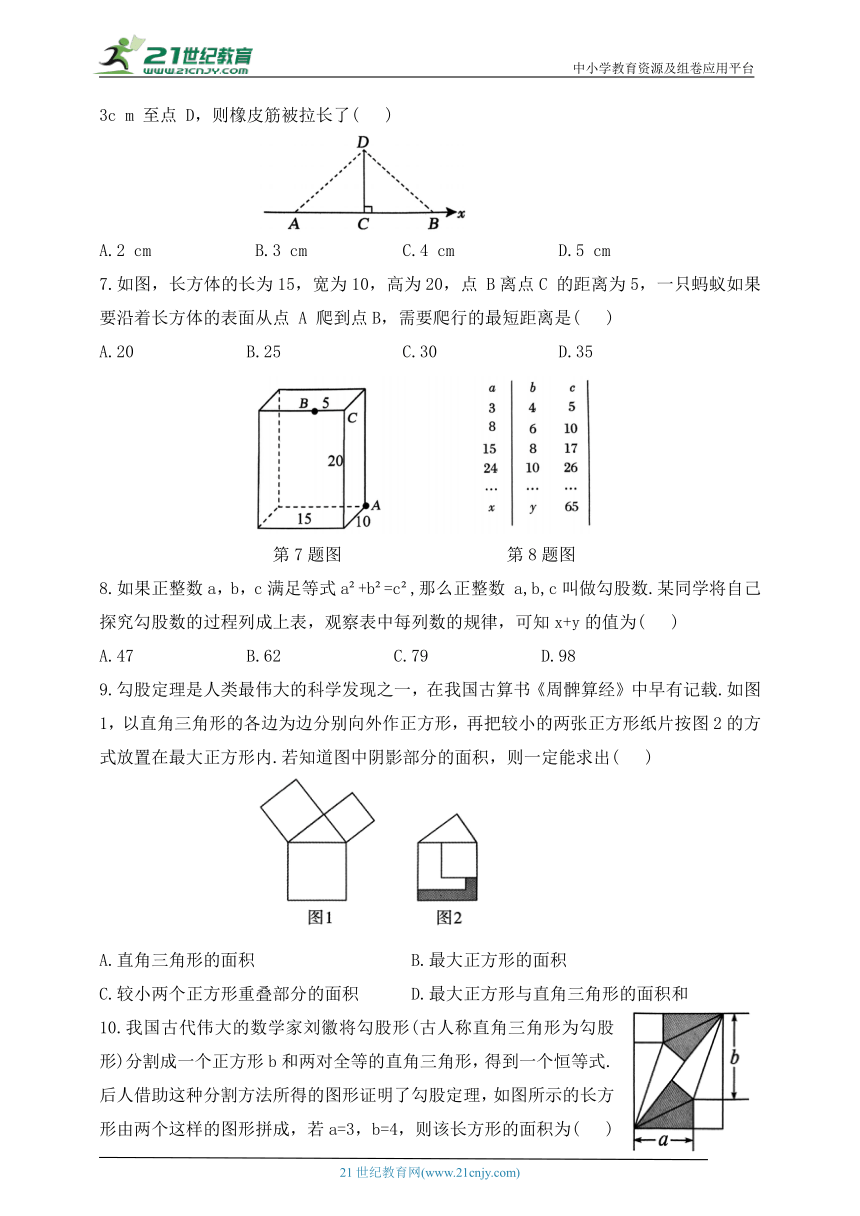
6.如图,长为 8cm 的橡皮筋放置在x轴上,固定两端A 和B,然后把中点C向上拉升3c m 至点 D,则橡皮筋被拉长了( )
A.2 cm B.3 cm C.4 cm D.5 cm
7.如图,长方体的长为15,宽为10,高为20,点 B离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点 A 爬到点B,需要爬行的最短距离是( )
A.20 B.25 C.30 D.35
第7题图 第8题图
8.如果正整数a,b,c满足等式a +b =c ,那么正整数 a,b,c叫做勾股数.某同学将自己探究勾股数的过程列成上表,观察表中每列数的规律,可知x+y的值为( )
A.47 B.62 C.79 D.98
9.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A.直角三角形的面积 B.最大正方形的面积
C.较小两个正方形重叠部分的面积 D.最大正方形与直角三角形的面积和
10.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形b和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的长方形由两个这样的图形拼成,若a=3,b=4,则该长方形的面积为( )
A.20 B.24
二、填空题(每小题5分,共30分)
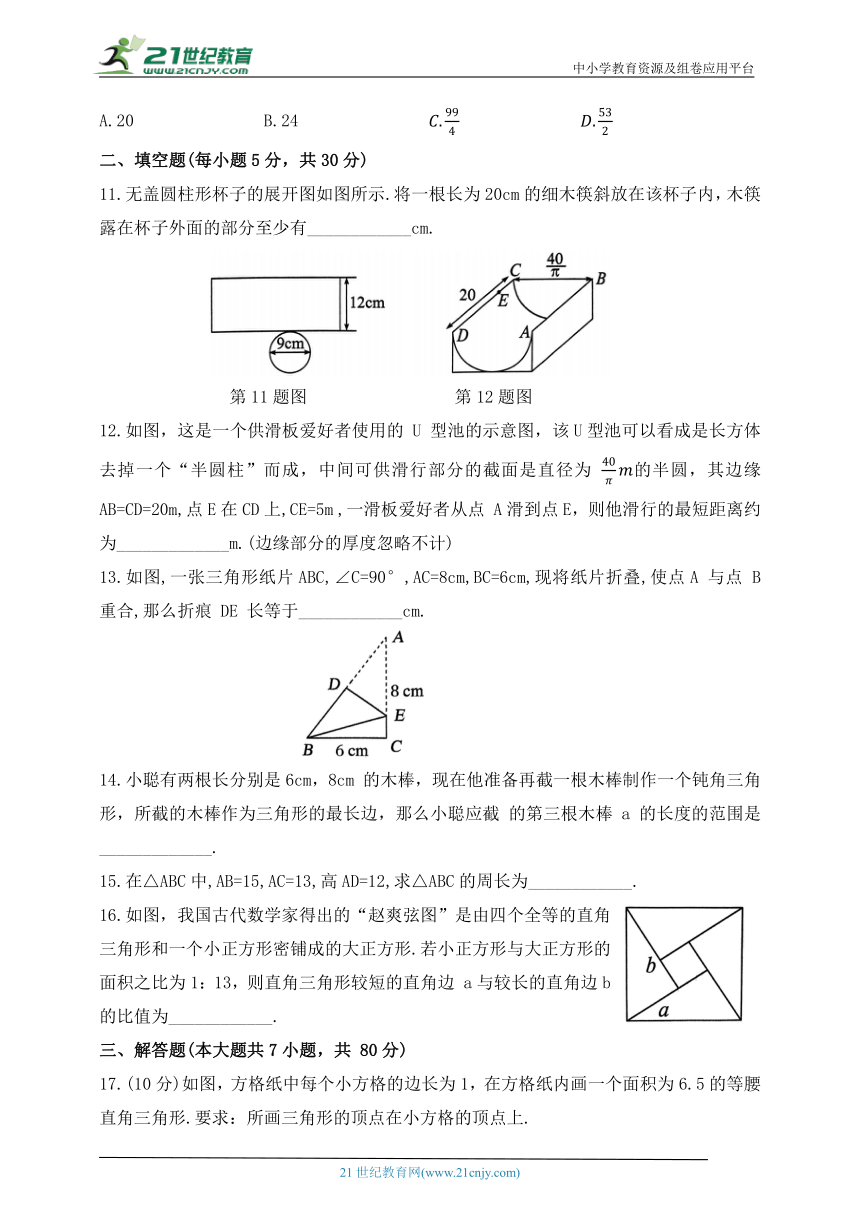
11.无盖圆柱形杯子的展开图如图所示.将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有____________cm.
第11题图 第12题图
12.如图,这是一个供滑板爱好者使用的 U 型池的示意图,该U型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为 的半圆,其边缘AB=CD=20m,点E在CD上,CE=5m ,一滑板爱好者从点 A滑到点E,则他滑行的最短距离约为_____________m.(边缘部分的厚度忽略不计)
13.如图,一张三角形纸片ABC,∠C=90°,AC=8cm,BC=6cm,现将纸片折叠,使点A 与点 B重合,那么折痕 DE 长等于____________cm.
14.小聪有两根长分别是6cm,8cm 的木棒,现在他准备再截一根木棒制作一个钝角三角形,所截的木棒作为三角形的最长边,那么小聪应截 的第三根木棒 a 的长度的范围是_____________.
15.在△ABC中,AB=15,AC=13,高AD=12,求△ABC的周长为____________.
16.如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺成的大正方形.若小正方形与大正方形的面积之比为1:13,则直角三角形较短的直角边 a与较长的直角边b的比值为____________.
三、解答题(本大题共7小题,共 80分)
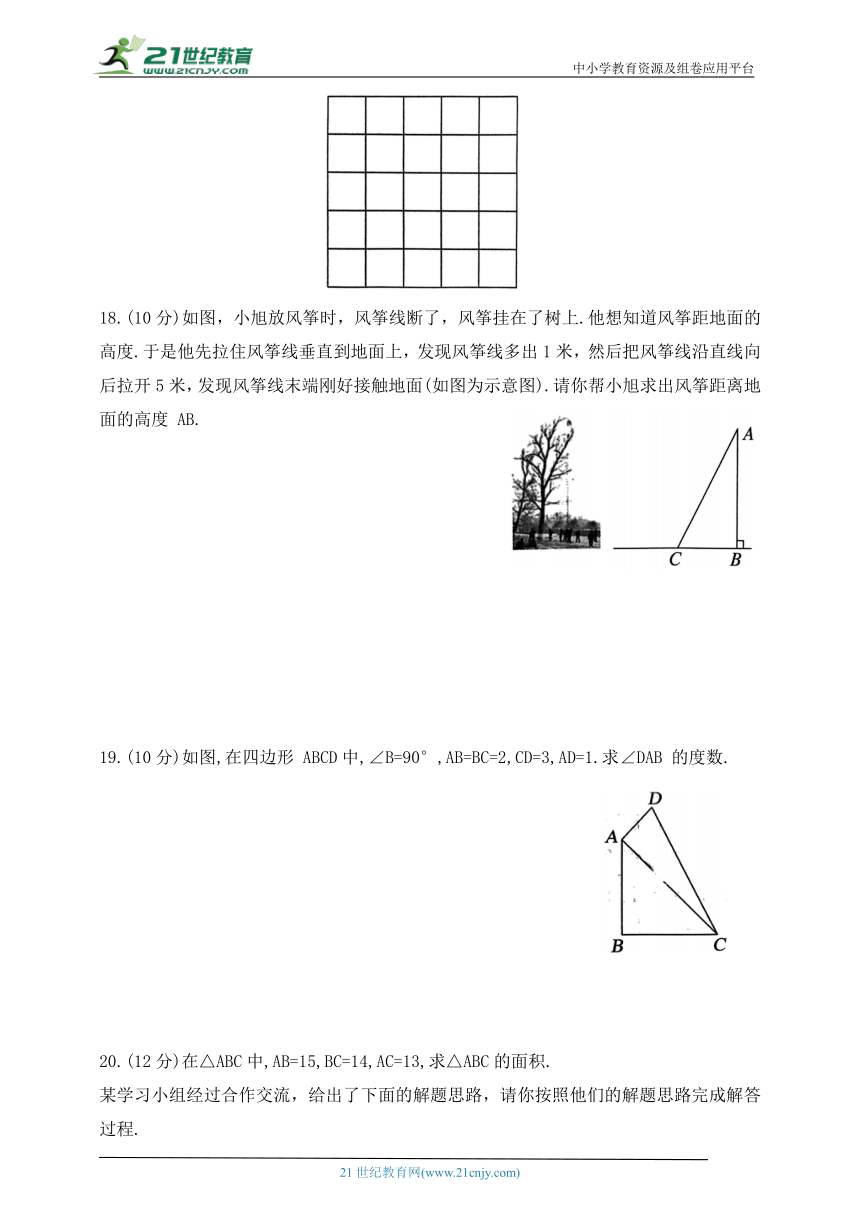
17.(10分)如图,方格纸中每个小方格的边长为1,在方格纸内画一个面积为6.5的等腰直角三角形.要求:所画三角形的顶点在小方格的顶点上.
18.(10分)如图,小旭放风筝时,风筝线断了,风筝挂在了树上.他想知道风筝距地面的高度.于是他先拉住风筝线垂直到地面上,发现风筝线多出1米,然后把风筝线沿直线向后拉开5米,发现风筝线末端刚好接触地面(如图为示意图).请你帮小旭求出风筝距离地面的高度 AB.
19.(10分)如图,在四边形 ABCD中,∠B=90°,AB=BC=2,CD=3,AD=1.求∠DAB 的度数.
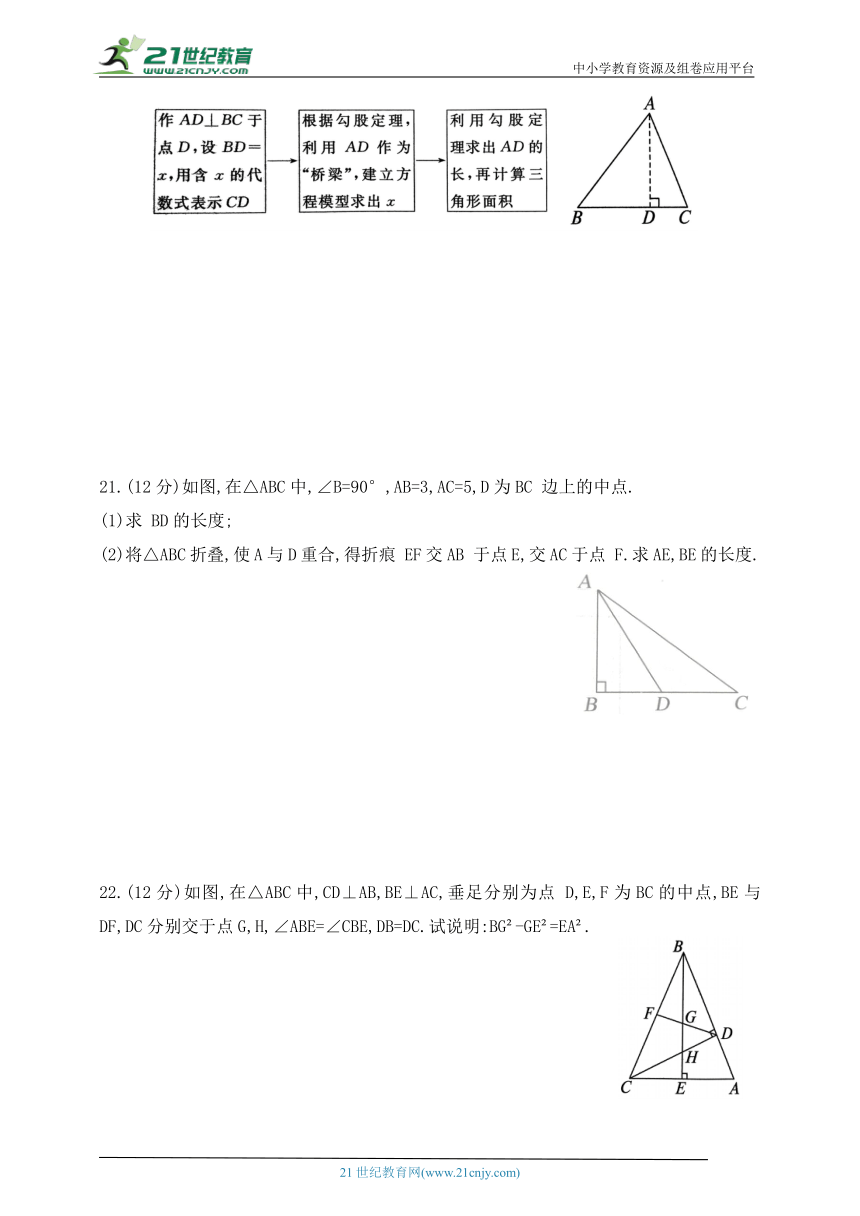
20.(12分)在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
21.(12分)如图,在△ABC中,∠B=90°,AB=3,AC=5,D为BC 边上的中点.
(1)求 BD的长度;
(2)将△ABC折叠,使A与D重合,得折痕 EF交AB 于点E,交AC于点 F.求AE,BE的长度.
22.(12分)如图,在△ABC中,CD⊥AB,BE⊥AC,垂足分别为点 D,E,F为BC的中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE,DB=DC.试说明:BG -GE =EA .
23.(14分)勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
(1)①请叙述勾股定理;
②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)
(2)①如图 4,5,6,以直角三角形的三边为边或直径,分别向外部作正方形,半圆,等边三角形,这三个图形中面积关系满足S +S =S 的有__________个;
②如图7所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为 S ,S ,直角三角形的面积为 S ,请判断 S ,S ,S 的关系并证明.
参考答案
一、选择题
1. C【解析】A.5 +4 ≠6 ,可知其不能构成直角三角形;B.5 +3 ≠6 ,可知其不能构成直角三角形;(C.6 +8 =10 ,可知其能构成直角三角形;;D.5 +12 ≠14 ,可知其不能构成直角三角形.故选C.
2. A
3. B【解析】图 1与图2中的k均为5.
4. B【解析】因为四边形 ABCD是长方形,所以∠ABC=90°.设AB=7a米,则BC=2a米.
在Rt△ABC中,由勾股定理,得(7a) +(2a) =4.77.化简得a =0.09,所以a=0.3.
所以BC=2a=0.6米.故选 B.
5. B【解析】①正确;②不能确定已知长度的两边是直角边或斜边,因此斜边不一定是5,故错误;③两较小边的平方和不等于最大边的平方,所以三角形不是直角三角形,所以错误;④由勾股定理可判断正确.综上①④正确,故选B.
6. A 【解析】在 Rt△ACD中, 根据勾股定理,得AD=5cm.所以AD+BD-AB=2AD-AB=10-8=2(cm),故橡皮筋被拉长了 2cm.
7. B 【解析】将长方体如图展开时有最短爬行距离,连接AB,根据两点之间线段最短,如图,BD=10+5=15,AD=20,由勾股定理得AB=25.
8. C【解析】由题可得 所以a=n -1,b=2n,c=n +1.
所以当c=n +1=65时,n=8.所以x=63,y=16.所以x+y=79.
9. C 【解析】设直角三角形的斜边长为c,较长直角边为b,较短直角边为a,由勾股定理,得c =a +b .阴影部分的面积=c -b -a +重叠部分的面积=重叠部分的面积.
故选 C.
10. B 【解析】设小正方形的边长为x,因为a=3,b=4,所以AB=3+4=7.在 Rt△ABC中,AC +BC =AB ,即(3+x) +(x+4) =7 .
整理,得x +7x-12=0,x +7x=12.
该长方形的面积=(x+3)(x+4)=x +7x+12=24.故选B.
二、填空题
11.5 【解析】由勾股定理可得杯子内的筷子长度的最大值为15 cm,则筷子露在杯子外面的部分长度的最小值为20-15=5(cm).
12.25 【解析】如图是U型池的侧面展开图,
2=20(m),DE=CD-CE=20-5=15(m).
在Rt△ADE中,AE =AD +DE =20 +15 =625.所以AE=25 m.
故他滑行的最短距离约为 25 m.
13. 【解析】在 Rt△ABC中,因为AC=8cm,BC=6cm,根据勾股定理,得AB=10cm.设CE=xcm,由折叠的性质得BD=AD=5cm ,BE=AE=(8-x) cm.
在Rt△BCE中,根据勾股定理可知BC +CE =BE ,即6 +x =(8-x) ,解得
则 在Rt△ADE中,由勾股定理,得
14.10cm<a<14 cm 【解析】若为直角三角形,则斜边为10cm,所以钝角三角形的最长边大于10 cm.由三角形三边关系得钝角三角形的最长边小于 14 cm.所以小聪应截的第三根木棒a的长度的范围是10 cm<a<14 cm.
15.42或32 【解析】如图1,当AD在△ABC的内部时,由勾股定理可分别求得BD=9,DC=5,所以△ABC 的周长为42.如图2,当AD在△ABC的外部时,同理可求得△ABC的周长为32.
16. 【解析】因为小正方形与大正方形的面积之比为1:13,所以设小正方形的面积为k ,则大正方形的面积为13k ,分别用a,b表示直角三角形的两直角边长,得(b-a) =k ,a +b =13k ,即a +b -2ab=13k -2ab=k .所以ab=6k .所以(a+b) =25k .所以b-a=k,a+b=5k,解得a=2k,b=3k.所以直角三角形较短的直角边 a与较长的直角边b的比值为
三、解答题
17.解:如图,画一个直角边长的平方为 13 的等腰直角三角形.
18.解:设AB=x米,则AC=(x+1)米.
由题意可得∠ABC=90°,BC=5米,
在Rt△ABC中,.AB +BC =AC ,即x +5 =(x+1) .解得x=12.
答:风筝距离地面的高度AB为 12米.
19.解:因为∠B=90°,AB=BC=2,所以AC =AB +BC =8,∠BAC=45°.
又因为 CD=3,AD=1,所以AC +AD =8+1=9,CD =9.所以AC +AD =CD .所以△ACD是直角三角形.所以∠CAD=90°.所以∠DAB=45°+90°=135°.
故∠DAB的度数为135°.
20.解:在△ABC中,AB=15,BC=14,AC=13,设BD=x,则CD=14-x.
在 Rt△ABD中,由勾股定理,得AD = AB -BD =15 -x .
在Rt△ADC中,由勾股定理得,AD =AC -CD =13 -(14-x) .
所以15 -x =13 -(14-x) .解得x=9.所以AD=12.
所以
21.解:(1)在△ABC中,因为∠B=90°,AB=3,AC=5,
所以BC =AC -AB =5 -3 =16.所以 BC=4.
又因为D为BC 边上的中点,所以
(2)△ABC折叠后如图所示,EF为折痕.
设AE=x,则DE=x,BE=3-x.
在 Rt△BDE中,BE +BD =DE ,即(3-x) +2 =x ,解得
所以 所以
22.解:如图,连接CG.
因为DB=DC,F为BC的中点,所以 DF垂直平分 BC.所以 BG=CG.
因为BE⊥AC,所以∠AEB=∠CEB.
在△ABE和△CBE中,因为∠AEB=∠CEB,BE=BE,∠ABE=∠CBE,所以△ABE≌△CBE(ASA).所
以EA=EC.
在 Rt△CGE中,由勾股定理,得CG -GE =CE .所以BG -GE =EA .
23.解:(1)①如果直角三角形的两条直角边分别为a,b,斜边为c,那么a +b =c .(或者:在直角三角形中,两条直角边的平方和等于斜边的平方.)
②证明:在图1中, 化简,得a +b =c .
在图2中 化简,得a +b =c .
在图3中 化简,得a +b =c .
(2)① 3
②结论:S +S =S .
证明:因为
所以
因为a +b =c ,所以S +S =S .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 勾股定理
单元测试卷
(时间:120分钟 分值:150分)
一、选择题(每小题 4分,共 40分)
1.以下列各组数为边长的三角形,其中能构成直角三角形的一组是( )
A.4,5,6 B.3,5,6 C.6,8,10 D.5,12,14
2.如图所示的是由两个直角三角形和三个正方形组成的图形,其中阴影部分的面积是( )
A.50 B.16 C.25 D.41
3.如图,边长k等于5的直角三角形有( )
A.1个 B.2个 C.3个 D.4个
4.图1是某品牌畅销的冰箱,图2 是它的侧面长方形示意图,对角线AC =4.77平方米,高 AB与宽BC 的长度比为7:2,则冰箱的宽 BC 的长度为( )
A.0.5米 B.0.6米 C.0.7米 D.0.8米
5.下列说法:①如果a,b,c为一组勾股数,那么4a,4b,4c仍是勾股数;②如果直角三角形的两边是 3,4,那么斜边必是5;③如果一个三角形的三边是 12,25,21,那么此三角形必是直角三角形;④一个等腰直角三角形的三边是 a,b,c(a>b=c),那么a2:b2:c2=2:1:1.其中正确的是( )
A.①② B.①④ C.①③ D.②④
6.如图,长为 8cm 的橡皮筋放置在x轴上,固定两端A 和B,然后把中点C向上拉升3c m 至点 D,则橡皮筋被拉长了( )
A.2 cm B.3 cm C.4 cm D.5 cm
7.如图,长方体的长为15,宽为10,高为20,点 B离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点 A 爬到点B,需要爬行的最短距离是( )
A.20 B.25 C.30 D.35
第7题图 第8题图
8.如果正整数a,b,c满足等式a +b =c ,那么正整数 a,b,c叫做勾股数.某同学将自己探究勾股数的过程列成上表,观察表中每列数的规律,可知x+y的值为( )
A.47 B.62 C.79 D.98
9.勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A.直角三角形的面积 B.最大正方形的面积
C.较小两个正方形重叠部分的面积 D.最大正方形与直角三角形的面积和
10.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形b和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的长方形由两个这样的图形拼成,若a=3,b=4,则该长方形的面积为( )
A.20 B.24
二、填空题(每小题5分,共30分)
11.无盖圆柱形杯子的展开图如图所示.将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有____________cm.
第11题图 第12题图
12.如图,这是一个供滑板爱好者使用的 U 型池的示意图,该U型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为 的半圆,其边缘AB=CD=20m,点E在CD上,CE=5m ,一滑板爱好者从点 A滑到点E,则他滑行的最短距离约为_____________m.(边缘部分的厚度忽略不计)
13.如图,一张三角形纸片ABC,∠C=90°,AC=8cm,BC=6cm,现将纸片折叠,使点A 与点 B重合,那么折痕 DE 长等于____________cm.
14.小聪有两根长分别是6cm,8cm 的木棒,现在他准备再截一根木棒制作一个钝角三角形,所截的木棒作为三角形的最长边,那么小聪应截 的第三根木棒 a 的长度的范围是_____________.
15.在△ABC中,AB=15,AC=13,高AD=12,求△ABC的周长为____________.
16.如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺成的大正方形.若小正方形与大正方形的面积之比为1:13,则直角三角形较短的直角边 a与较长的直角边b的比值为____________.
三、解答题(本大题共7小题,共 80分)
17.(10分)如图,方格纸中每个小方格的边长为1,在方格纸内画一个面积为6.5的等腰直角三角形.要求:所画三角形的顶点在小方格的顶点上.
18.(10分)如图,小旭放风筝时,风筝线断了,风筝挂在了树上.他想知道风筝距地面的高度.于是他先拉住风筝线垂直到地面上,发现风筝线多出1米,然后把风筝线沿直线向后拉开5米,发现风筝线末端刚好接触地面(如图为示意图).请你帮小旭求出风筝距离地面的高度 AB.
19.(10分)如图,在四边形 ABCD中,∠B=90°,AB=BC=2,CD=3,AD=1.求∠DAB 的度数.
20.(12分)在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
21.(12分)如图,在△ABC中,∠B=90°,AB=3,AC=5,D为BC 边上的中点.
(1)求 BD的长度;
(2)将△ABC折叠,使A与D重合,得折痕 EF交AB 于点E,交AC于点 F.求AE,BE的长度.
22.(12分)如图,在△ABC中,CD⊥AB,BE⊥AC,垂足分别为点 D,E,F为BC的中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE,DB=DC.试说明:BG -GE =EA .
23.(14分)勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
(1)①请叙述勾股定理;
②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)
(2)①如图 4,5,6,以直角三角形的三边为边或直径,分别向外部作正方形,半圆,等边三角形,这三个图形中面积关系满足S +S =S 的有__________个;
②如图7所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为 S ,S ,直角三角形的面积为 S ,请判断 S ,S ,S 的关系并证明.
参考答案
一、选择题
1. C【解析】A.5 +4 ≠6 ,可知其不能构成直角三角形;B.5 +3 ≠6 ,可知其不能构成直角三角形;(C.6 +8 =10 ,可知其能构成直角三角形;;D.5 +12 ≠14 ,可知其不能构成直角三角形.故选C.
2. A
3. B【解析】图 1与图2中的k均为5.
4. B【解析】因为四边形 ABCD是长方形,所以∠ABC=90°.设AB=7a米,则BC=2a米.
在Rt△ABC中,由勾股定理,得(7a) +(2a) =4.77.化简得a =0.09,所以a=0.3.
所以BC=2a=0.6米.故选 B.
5. B【解析】①正确;②不能确定已知长度的两边是直角边或斜边,因此斜边不一定是5,故错误;③两较小边的平方和不等于最大边的平方,所以三角形不是直角三角形,所以错误;④由勾股定理可判断正确.综上①④正确,故选B.
6. A 【解析】在 Rt△ACD中, 根据勾股定理,得AD=5cm.所以AD+BD-AB=2AD-AB=10-8=2(cm),故橡皮筋被拉长了 2cm.
7. B 【解析】将长方体如图展开时有最短爬行距离,连接AB,根据两点之间线段最短,如图,BD=10+5=15,AD=20,由勾股定理得AB=25.
8. C【解析】由题可得 所以a=n -1,b=2n,c=n +1.
所以当c=n +1=65时,n=8.所以x=63,y=16.所以x+y=79.
9. C 【解析】设直角三角形的斜边长为c,较长直角边为b,较短直角边为a,由勾股定理,得c =a +b .阴影部分的面积=c -b -a +重叠部分的面积=重叠部分的面积.
故选 C.
10. B 【解析】设小正方形的边长为x,因为a=3,b=4,所以AB=3+4=7.在 Rt△ABC中,AC +BC =AB ,即(3+x) +(x+4) =7 .
整理,得x +7x-12=0,x +7x=12.
该长方形的面积=(x+3)(x+4)=x +7x+12=24.故选B.
二、填空题
11.5 【解析】由勾股定理可得杯子内的筷子长度的最大值为15 cm,则筷子露在杯子外面的部分长度的最小值为20-15=5(cm).
12.25 【解析】如图是U型池的侧面展开图,
2=20(m),DE=CD-CE=20-5=15(m).
在Rt△ADE中,AE =AD +DE =20 +15 =625.所以AE=25 m.
故他滑行的最短距离约为 25 m.
13. 【解析】在 Rt△ABC中,因为AC=8cm,BC=6cm,根据勾股定理,得AB=10cm.设CE=xcm,由折叠的性质得BD=AD=5cm ,BE=AE=(8-x) cm.
在Rt△BCE中,根据勾股定理可知BC +CE =BE ,即6 +x =(8-x) ,解得
则 在Rt△ADE中,由勾股定理,得
14.10cm<a<14 cm 【解析】若为直角三角形,则斜边为10cm,所以钝角三角形的最长边大于10 cm.由三角形三边关系得钝角三角形的最长边小于 14 cm.所以小聪应截的第三根木棒a的长度的范围是10 cm<a<14 cm.
15.42或32 【解析】如图1,当AD在△ABC的内部时,由勾股定理可分别求得BD=9,DC=5,所以△ABC 的周长为42.如图2,当AD在△ABC的外部时,同理可求得△ABC的周长为32.
16. 【解析】因为小正方形与大正方形的面积之比为1:13,所以设小正方形的面积为k ,则大正方形的面积为13k ,分别用a,b表示直角三角形的两直角边长,得(b-a) =k ,a +b =13k ,即a +b -2ab=13k -2ab=k .所以ab=6k .所以(a+b) =25k .所以b-a=k,a+b=5k,解得a=2k,b=3k.所以直角三角形较短的直角边 a与较长的直角边b的比值为
三、解答题
17.解:如图,画一个直角边长的平方为 13 的等腰直角三角形.
18.解:设AB=x米,则AC=(x+1)米.
由题意可得∠ABC=90°,BC=5米,
在Rt△ABC中,.AB +BC =AC ,即x +5 =(x+1) .解得x=12.
答:风筝距离地面的高度AB为 12米.
19.解:因为∠B=90°,AB=BC=2,所以AC =AB +BC =8,∠BAC=45°.
又因为 CD=3,AD=1,所以AC +AD =8+1=9,CD =9.所以AC +AD =CD .所以△ACD是直角三角形.所以∠CAD=90°.所以∠DAB=45°+90°=135°.
故∠DAB的度数为135°.
20.解:在△ABC中,AB=15,BC=14,AC=13,设BD=x,则CD=14-x.
在 Rt△ABD中,由勾股定理,得AD = AB -BD =15 -x .
在Rt△ADC中,由勾股定理得,AD =AC -CD =13 -(14-x) .
所以15 -x =13 -(14-x) .解得x=9.所以AD=12.
所以
21.解:(1)在△ABC中,因为∠B=90°,AB=3,AC=5,
所以BC =AC -AB =5 -3 =16.所以 BC=4.
又因为D为BC 边上的中点,所以
(2)△ABC折叠后如图所示,EF为折痕.
设AE=x,则DE=x,BE=3-x.
在 Rt△BDE中,BE +BD =DE ,即(3-x) +2 =x ,解得
所以 所以
22.解:如图,连接CG.
因为DB=DC,F为BC的中点,所以 DF垂直平分 BC.所以 BG=CG.
因为BE⊥AC,所以∠AEB=∠CEB.
在△ABE和△CBE中,因为∠AEB=∠CEB,BE=BE,∠ABE=∠CBE,所以△ABE≌△CBE(ASA).所
以EA=EC.
在 Rt△CGE中,由勾股定理,得CG -GE =CE .所以BG -GE =EA .
23.解:(1)①如果直角三角形的两条直角边分别为a,b,斜边为c,那么a +b =c .(或者:在直角三角形中,两条直角边的平方和等于斜边的平方.)
②证明:在图1中, 化简,得a +b =c .
在图2中 化简,得a +b =c .
在图3中 化简,得a +b =c .
(2)① 3
②结论:S +S =S .
证明:因为
所以
因为a +b =c ,所以S +S =S .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
