十字相乘法[上学期]
图片预览




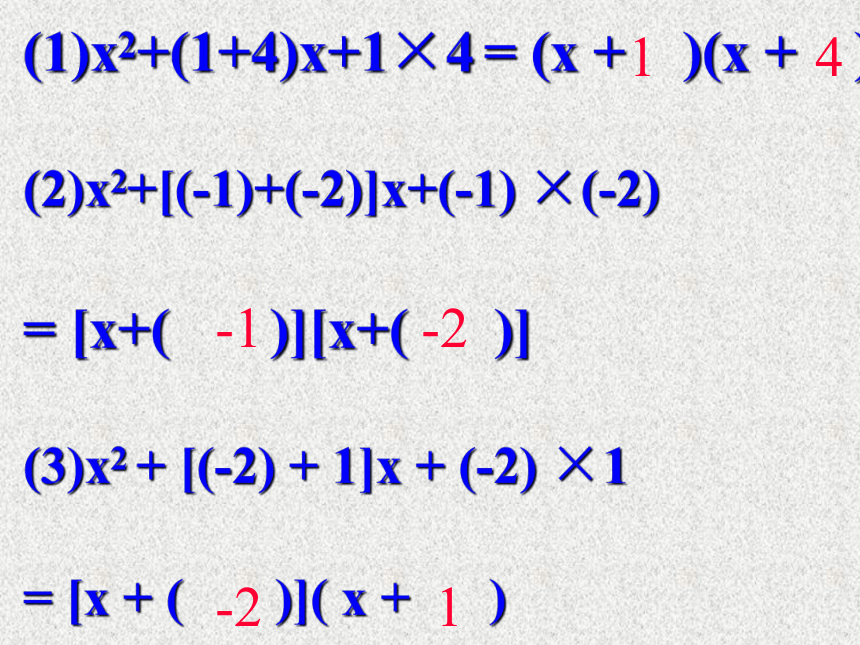
文档简介
课件11张PPT。十字相乘法分解因式新建中学 x2 + (a+b)x + a b型式子的因式分解学习目标:
1.掌握公式x2 + ( a + b) x + a b =(x + a) ( x + b )
2、运用公式会对x2 + (a+b)x + a b型的二次三项式进行因式分解。1、计算(1)(x +1) ( x + 2 )
(2)(x -1) ( x + 2 )
(3)(x + a) ( x + b )= x2 + ( 1 + 2 )x + 1×2= x2 +[(-1) + 2]x + (-1)×2= x2 + ( a + b )x + a b2、下列各式能因式分解吗?(1) x2 + ( 1 + 2 )x + 1×2
(2) x2 +[(-1)+2]x+(-1)×2
(3) x2 + ( a + b )x + a b
= (x +1) ( x + 2 )= (x -1) ( x + 2 )= (x + a) ( x + b )3、公式推导x2 + ( a + b )x + a b= x2 + ax + bx + ab= x(x + a) + b(x + a)= (x + a) (x + b)∴ x2 + ( a + b )x + a b = (x + a) (x + b)
4、运用公式必须同时具备的三个条件:(1)二次项系数式是1的二次三项式(2)常数项是两个数之积(3)一次项系数是常数项的两个因数之和(1)x2+(1+4)x+1×4 = (x + )(x + )
(2)x2+[(-1)+(-2)]x+(-1) ×(-2)
= [x+( )][x+( )]
(3)x2 + [(-2) + 1]x + (-2) ×1
= [x + ( )]( x + )1 4-1 -2-2 1 例1:分解因式
(1)x2+3x+2 (2)x2 -7x+6分析: (1)二次项系数为1,常数项2=1×2 == 1+2=(-1)×(-2),≠一次项系数3 (-1)+(-2)(1)解: x2+3x+2 =(x+1)(x+2)分析:(2)二次项系数为1,常数项6=2×3=1×6=(-1)×(-6)=(-2) ×(-3),一次项系数-7≠(-2) +(-3)≠2+3=(-1)+(-6) 1.常数项是正数时,它分解成两个同号因数,它们和一次项系数符号相同。因式分解时常数项因数分解的一般规律:(1)解: x2 -7x+6
=(x-1)(x-6)例2. 分解因式
(1)x2+x-2 (2)x2-2x-15分析:(1)二次项系数为1,常数项-2=(-1) ×2 =1× (-2),一次项系数1≠1+(-2) (1)解: x2+x-2 =(-1) +2
分析: (2)二次项系数为1,常数项-15=1×(-15)=(-1) ×15
=3×(-5)=(-3) ×5,一次项系数-2≠(-3) +5 =3+(-5)(2)解: x2-2x-15=(x+3)(x-5) 2.常数项是负数时,它分解成两个异号因数,其中绝对值较大的因数和一次项系数符号相同。=(x-1)(x+2)=(x-3)(3x-1)=(5x+3)(x-4)因式分解
(1)x2+6x+8 (2)y2+7y+12
(3)x2-5x+4 (4)x2+2x-8
(5)x2-2x-8 (6)y2-7y-18
(7)a2b2-a b-2 (8)+小结:
1.运用公式x2 + ( a + b )x + a b = (x + a) (x + b)
必须同时具备的三个条件:(1)二次项系数式是1的二次三项式(2)常数项是两个数之积(3)一次项系数是常数项的两个因数之和 2.常数项因数分解的一般规律:
(1) 常数项是正数时,它分解成两个同号因数,它们和一次项系数符号相同。
(2) 常数项是负数时,它分解成两个异号因数,其中绝对值较大的因数和一次项系数符号相同。
谢谢再见
1.掌握公式x2 + ( a + b) x + a b =(x + a) ( x + b )
2、运用公式会对x2 + (a+b)x + a b型的二次三项式进行因式分解。1、计算(1)(x +1) ( x + 2 )
(2)(x -1) ( x + 2 )
(3)(x + a) ( x + b )= x2 + ( 1 + 2 )x + 1×2= x2 +[(-1) + 2]x + (-1)×2= x2 + ( a + b )x + a b2、下列各式能因式分解吗?(1) x2 + ( 1 + 2 )x + 1×2
(2) x2 +[(-1)+2]x+(-1)×2
(3) x2 + ( a + b )x + a b
= (x +1) ( x + 2 )= (x -1) ( x + 2 )= (x + a) ( x + b )3、公式推导x2 + ( a + b )x + a b= x2 + ax + bx + ab= x(x + a) + b(x + a)= (x + a) (x + b)∴ x2 + ( a + b )x + a b = (x + a) (x + b)
4、运用公式必须同时具备的三个条件:(1)二次项系数式是1的二次三项式(2)常数项是两个数之积(3)一次项系数是常数项的两个因数之和(1)x2+(1+4)x+1×4 = (x + )(x + )
(2)x2+[(-1)+(-2)]x+(-1) ×(-2)
= [x+( )][x+( )]
(3)x2 + [(-2) + 1]x + (-2) ×1
= [x + ( )]( x + )1 4-1 -2-2 1 例1:分解因式
(1)x2+3x+2 (2)x2 -7x+6分析: (1)二次项系数为1,常数项2=1×2 == 1+2=(-1)×(-2),≠一次项系数3 (-1)+(-2)(1)解: x2+3x+2 =(x+1)(x+2)分析:(2)二次项系数为1,常数项6=2×3=1×6=(-1)×(-6)=(-2) ×(-3),一次项系数-7≠(-2) +(-3)≠2+3=(-1)+(-6) 1.常数项是正数时,它分解成两个同号因数,它们和一次项系数符号相同。因式分解时常数项因数分解的一般规律:(1)解: x2 -7x+6
=(x-1)(x-6)例2. 分解因式
(1)x2+x-2 (2)x2-2x-15分析:(1)二次项系数为1,常数项-2=(-1) ×2 =1× (-2),一次项系数1≠1+(-2) (1)解: x2+x-2 =(-1) +2
分析: (2)二次项系数为1,常数项-15=1×(-15)=(-1) ×15
=3×(-5)=(-3) ×5,一次项系数-2≠(-3) +5 =3+(-5)(2)解: x2-2x-15=(x+3)(x-5) 2.常数项是负数时,它分解成两个异号因数,其中绝对值较大的因数和一次项系数符号相同。=(x-1)(x+2)=(x-3)(3x-1)=(5x+3)(x-4)因式分解
(1)x2+6x+8 (2)y2+7y+12
(3)x2-5x+4 (4)x2+2x-8
(5)x2-2x-8 (6)y2-7y-18
(7)a2b2-a b-2 (8)+小结:
1.运用公式x2 + ( a + b )x + a b = (x + a) (x + b)
必须同时具备的三个条件:(1)二次项系数式是1的二次三项式(2)常数项是两个数之积(3)一次项系数是常数项的两个因数之和 2.常数项因数分解的一般规律:
(1) 常数项是正数时,它分解成两个同号因数,它们和一次项系数符号相同。
(2) 常数项是负数时,它分解成两个异号因数,其中绝对值较大的因数和一次项系数符号相同。
谢谢再见
