4.3角 同步练习 2023-2024学年人教版七年级数学上册(含答案)
文档属性
| 名称 | 4.3角 同步练习 2023-2024学年人教版七年级数学上册(含答案) | 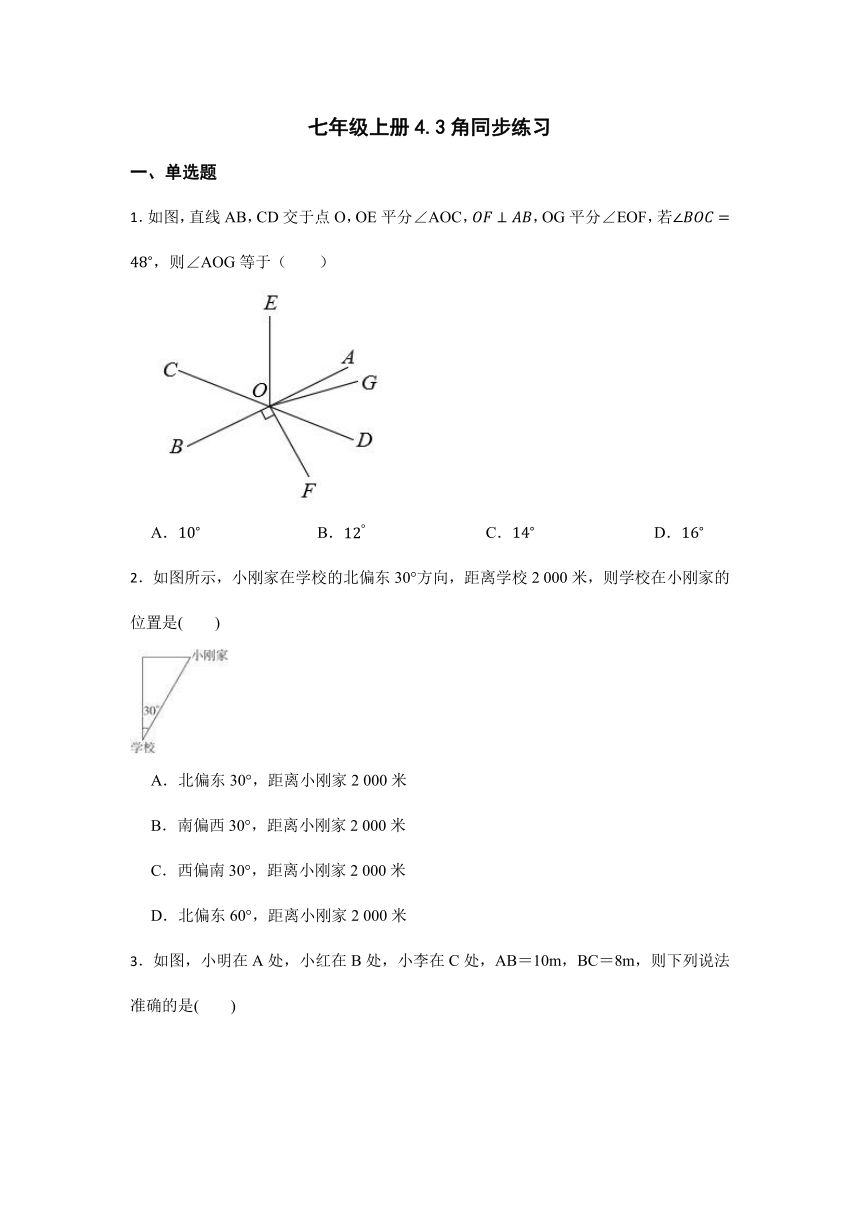 | |
| 格式 | docx | ||
| 文件大小 | 59.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-30 22:07:10 | ||
图片预览



文档简介
七年级上册4.3角同步练习
一、单选题
1.如图,直线AB,CD交于点O,OE平分∠AOC,,OG平分∠EOF,若,则∠AOG等于( )
A. B. C. D.
2.如图所示,小刚家在学校的北偏东30°方向,距离学校2 000米,则学校在小刚家的位置是( )
A.北偏东30°,距离小刚家2 000米
B.南偏西30°,距离小刚家2 000米
C.西偏南30°,距离小刚家2 000米
D.北偏东60°,距离小刚家2 000米
3.如图,小明在A处,小红在B处,小李在C处,AB=10m,BC=8m,则下列说法准确的是( )
A.小红在小明的北偏东35°方向
B.小红在小明的南偏西55°方向
C.小明在小红的南偏西55°方向,距离为10m处
D.小明在小李的北偏东35°方向,距离为18m处
4.如图,有三个小海岛A、B、C,其中海岛C到海岛A的距离为100海里,海岛B在海岛A北偏东70°的方向上,若海岛C在海岛B北偏西20°的方向上,且到海岛B的距离是50海里,则海岛C在海岛A( )
A.北偏东20°方向 B.北偏东30°方向
C.北偏东40°方向 D.北偏西30°方向
5.已知∠α=70°18',则∠α的补角是( )
A.110°42′ B.109°42′ C.20°42′ D.19°42′
6.用度、分,秒表示22.45°为( )
A.22°45′ B.22°30′ C.22°27′ D.22°20′
7.如图,直线AB与CD相交于点O,EO⊥CD,垂足为O,则图中∠AOE和∠BOD的关系是( )
A.相等 B.互补 C.互为对顶角 D.互余
8.如图,用尺规作出∠OBF=∠AOB,所画痕迹 是( )
A.以点B为圆心,OD为半径的弧 B.以点C为圆心,DC为半径的弧
C.以点E为圆心,OD为半径的弧 D.以点E为圆心,DC为半径的弧
9.已知点A在点B的北偏东30°方向,点B在点C的正西方向,则∠ABC的度数是( )
A.60° B.90° C.120° D.150°
10.钟表10点30分时,时针与分针所成的角是( )
A. B. C. D.
二、填空题
11.21°17′×5= .
12.如果一个角是60°,用10倍的望远镜观察,这个角应是 °
13.如图,已知AO⊥BC,DO⊥OE,若∠1=56°,则∠2= .
14.如图,A、O、B 在同一条直线上,如果 OA 的方向是北偏西 25°那么 OB 的方向是南偏东 .
15.32.48°= 度 分 秒.
三、解答题
16.如图, 是 内的两条射线, 平分 , ,若 , ,求 的度数.
17.一个角的补角比它的余角的二倍还多18度,这个角有多少度?
18.如图,直线 和 相交于点O, , 平分 , ,求 的度数.
19.如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.若∠BOC=62°,求∠DOE的度数.
20.如图, ,分别引射线 (点 在 外), 、 ,使 平分 , 平分 .若 ,求 的度数.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】C
7.【答案】D
8.【答案】D
9.【答案】A
10.【答案】B
11.【答案】106°25′
12.【答案】60
13.【答案】56°
14.【答案】25°
15.【答案】32;28;48
16.【答案】解:设∠BOE=x°,则∠DOB=55°﹣x°,
由∠BOE= ∠EOC可得∠EOC=2x°,
由OD平分∠AOB,
得∠AOB=2∠DOB,
故有2x+x+2(55﹣x)=150,
解方程得x=40,
故∠EOC=2x=80°.
17.【答案】解:设这个角的度数为x,则它的余角为(90°﹣x),补角为(180°﹣x),
依题意,得180°﹣x=2(90°﹣x)+18°
解得x=18°
答:这个角的度数为18°.
18.【答案】解:∵ OE⊥CD,
∴∠COE=90°,
∵∠COF=34°,
∴∠EOF=56°,
∵OF平分∠AOE,
∴∠AOF=∠FOE=56°,
∴ .
19.【答案】解:∵OD平分∠AOC,OE平分∠BOC,
∴
∴ .
20.【答案】解:如图,∵OD是∠BOC的平分线,
∴∠COD=∠BOD=20°,
∵OA⊥OB ,
∴∠AOB=90°
∴∠AOD=∠BOD+∠AOB=20°+90°=110°,
又∵OE是∠AOD的平分线,
∴∠DOE= ∠AOD=55°,
∴∠BOE=∠DOE-∠BOD=55°-20°=35°
一、单选题
1.如图,直线AB,CD交于点O,OE平分∠AOC,,OG平分∠EOF,若,则∠AOG等于( )
A. B. C. D.
2.如图所示,小刚家在学校的北偏东30°方向,距离学校2 000米,则学校在小刚家的位置是( )
A.北偏东30°,距离小刚家2 000米
B.南偏西30°,距离小刚家2 000米
C.西偏南30°,距离小刚家2 000米
D.北偏东60°,距离小刚家2 000米
3.如图,小明在A处,小红在B处,小李在C处,AB=10m,BC=8m,则下列说法准确的是( )
A.小红在小明的北偏东35°方向
B.小红在小明的南偏西55°方向
C.小明在小红的南偏西55°方向,距离为10m处
D.小明在小李的北偏东35°方向,距离为18m处
4.如图,有三个小海岛A、B、C,其中海岛C到海岛A的距离为100海里,海岛B在海岛A北偏东70°的方向上,若海岛C在海岛B北偏西20°的方向上,且到海岛B的距离是50海里,则海岛C在海岛A( )
A.北偏东20°方向 B.北偏东30°方向
C.北偏东40°方向 D.北偏西30°方向
5.已知∠α=70°18',则∠α的补角是( )
A.110°42′ B.109°42′ C.20°42′ D.19°42′
6.用度、分,秒表示22.45°为( )
A.22°45′ B.22°30′ C.22°27′ D.22°20′
7.如图,直线AB与CD相交于点O,EO⊥CD,垂足为O,则图中∠AOE和∠BOD的关系是( )
A.相等 B.互补 C.互为对顶角 D.互余
8.如图,用尺规作出∠OBF=∠AOB,所画痕迹 是( )
A.以点B为圆心,OD为半径的弧 B.以点C为圆心,DC为半径的弧
C.以点E为圆心,OD为半径的弧 D.以点E为圆心,DC为半径的弧
9.已知点A在点B的北偏东30°方向,点B在点C的正西方向,则∠ABC的度数是( )
A.60° B.90° C.120° D.150°
10.钟表10点30分时,时针与分针所成的角是( )
A. B. C. D.
二、填空题
11.21°17′×5= .
12.如果一个角是60°,用10倍的望远镜观察,这个角应是 °
13.如图,已知AO⊥BC,DO⊥OE,若∠1=56°,则∠2= .
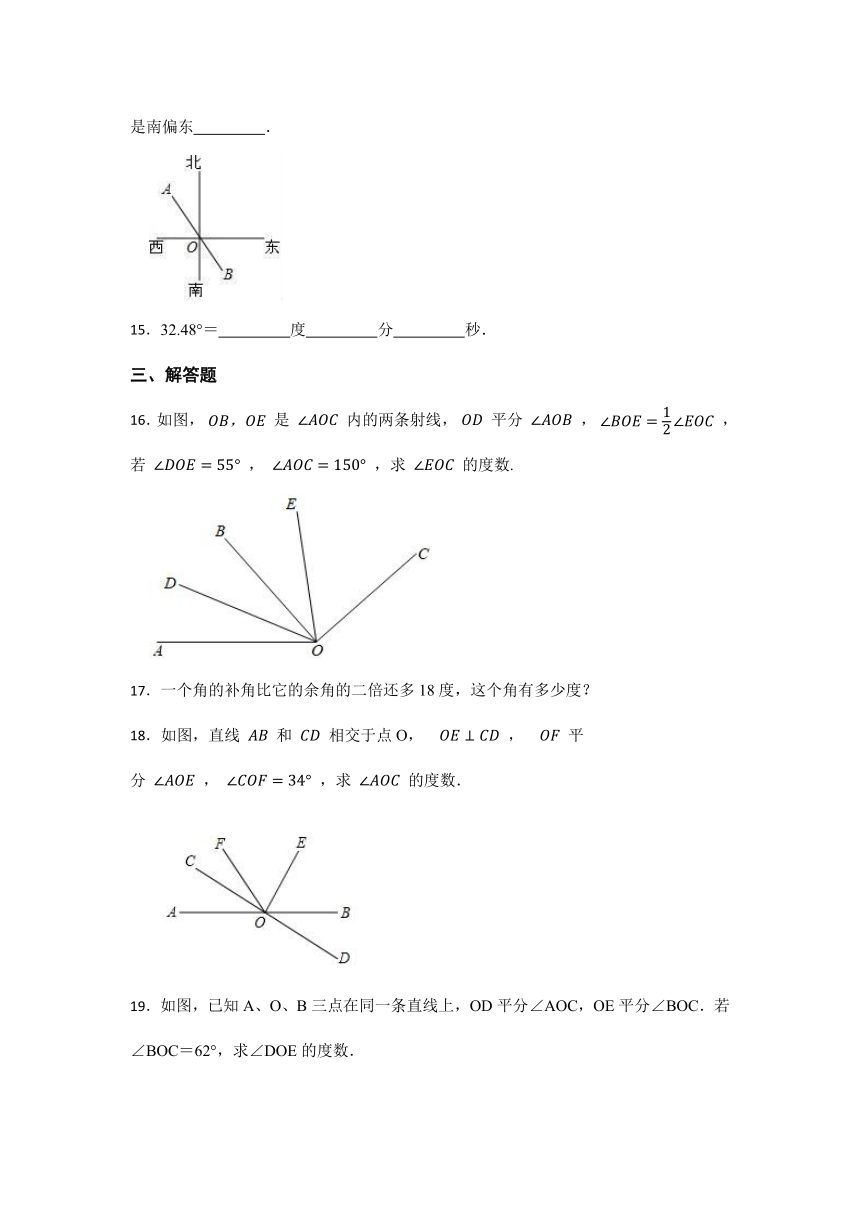
14.如图,A、O、B 在同一条直线上,如果 OA 的方向是北偏西 25°那么 OB 的方向是南偏东 .
15.32.48°= 度 分 秒.
三、解答题
16.如图, 是 内的两条射线, 平分 , ,若 , ,求 的度数.
17.一个角的补角比它的余角的二倍还多18度,这个角有多少度?
18.如图,直线 和 相交于点O, , 平分 , ,求 的度数.
19.如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.若∠BOC=62°,求∠DOE的度数.
20.如图, ,分别引射线 (点 在 外), 、 ,使 平分 , 平分 .若 ,求 的度数.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】C
7.【答案】D
8.【答案】D
9.【答案】A
10.【答案】B
11.【答案】106°25′
12.【答案】60
13.【答案】56°
14.【答案】25°
15.【答案】32;28;48
16.【答案】解:设∠BOE=x°,则∠DOB=55°﹣x°,
由∠BOE= ∠EOC可得∠EOC=2x°,
由OD平分∠AOB,
得∠AOB=2∠DOB,
故有2x+x+2(55﹣x)=150,
解方程得x=40,
故∠EOC=2x=80°.
17.【答案】解:设这个角的度数为x,则它的余角为(90°﹣x),补角为(180°﹣x),
依题意,得180°﹣x=2(90°﹣x)+18°
解得x=18°
答:这个角的度数为18°.
18.【答案】解:∵ OE⊥CD,
∴∠COE=90°,
∵∠COF=34°,
∴∠EOF=56°,
∵OF平分∠AOE,
∴∠AOF=∠FOE=56°,
∴ .
19.【答案】解:∵OD平分∠AOC,OE平分∠BOC,
∴
∴ .
20.【答案】解:如图,∵OD是∠BOC的平分线,
∴∠COD=∠BOD=20°,
∵OA⊥OB ,
∴∠AOB=90°
∴∠AOD=∠BOD+∠AOB=20°+90°=110°,
又∵OE是∠AOD的平分线,
∴∠DOE= ∠AOD=55°,
∴∠BOE=∠DOE-∠BOD=55°-20°=35°
