2.1直线的倾斜角与斜率 学案(含答案)
文档属性
| 名称 | 2.1直线的倾斜角与斜率 学案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 288.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-01 00:00:00 | ||
图片预览


文档简介
2.1 直线的倾斜角与斜率自学案
学习目标
在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素;
理解直线的倾斜角和斜率的概念,经历用代数方法刻画直线斜率的过程,掌握过两点直线斜率的计算公式;
能根据斜率判断两条直线平行或垂直;
掌握用代数方法研究直线的相关问题,体会数形结合的数学思想方法,发展数学思维,落实直观想象和数学运算的核心素养。
知识清单
直线的倾斜角和斜率
倾斜角定义:当直线与轴________时,以轴为基准,轴______与直线_______方向之间所成的_______叫做直线的_______。
当直线与轴_____或____时,它的倾斜角为_____;当直线与轴_____时,它的倾斜角为_____。直线倾斜角的取值范围是_________。
问:不同直线的倾斜角一定不相同吗?
斜率定义:若直线的倾斜角为,则______时,直线的斜率______;当______时,直线的斜率______。
斜率与倾斜角的对应关系
图示
倾斜角
斜率 k
问:直线的斜率一定随着倾斜角的增大而增大吗?
已知直线经过两点,若,则直线的斜率_______;若,则直线的斜率_______;
注:若已知两点的横坐标中含有参数,则需要对参数进行________,分类的依据就是____________________。
直线的方向向量与斜率的关系
当直线的斜率k存在时,直线的一个方向向量为_________;
当直线的一个方向向量为时,直线的斜率k=_________。
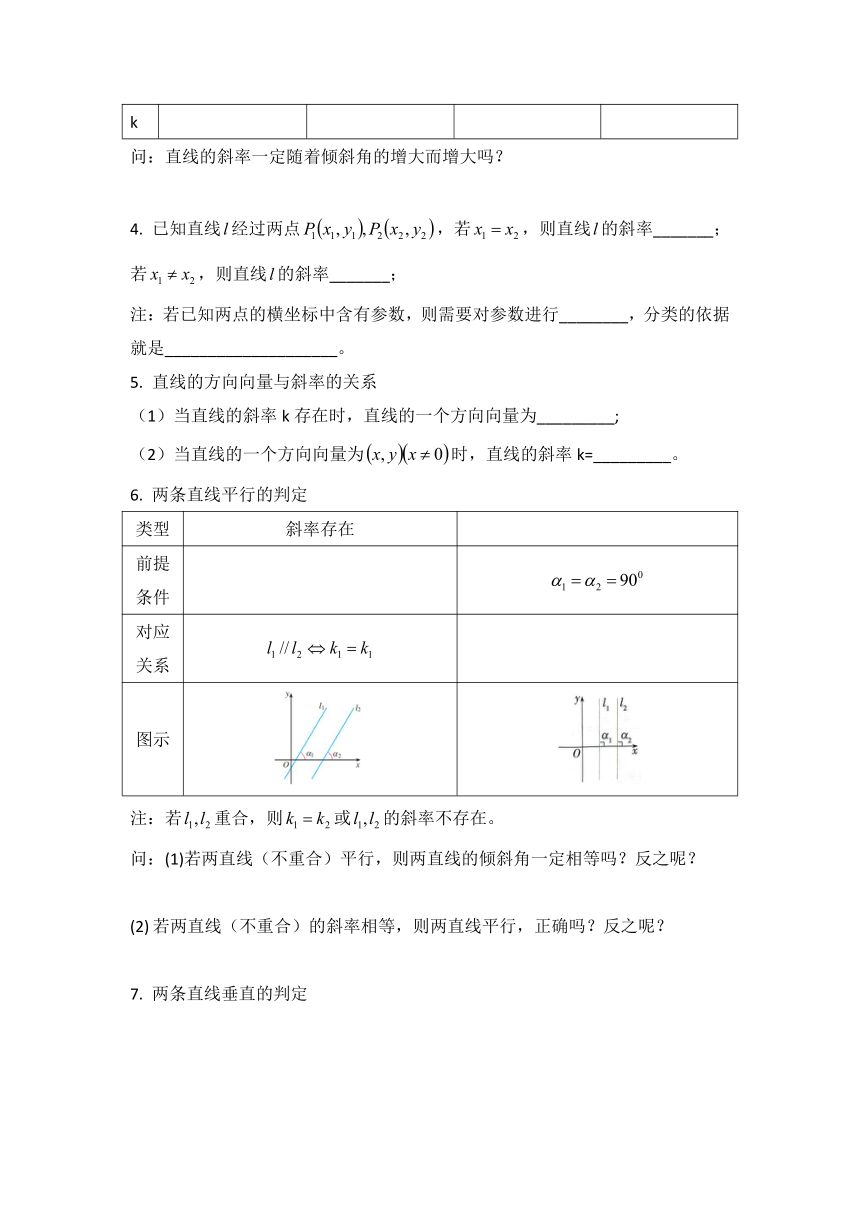
两条直线平行的判定
类型 斜率存在
前提 条件
对应 关系
图示
注:若重合,则或的斜率不存在。
问:(1)若两直线(不重合)平行,则两直线的倾斜角一定相等吗?反之呢?
若两直线(不重合)的斜率相等,则两直线平行,正确吗?反之呢?
两条直线垂直的判定
图示
对应关系
问:设直线的斜率为,直线垂直于直线,则直线的斜率为,此结论正确吗?
自我检测
2.1.1 倾斜角与斜率
1. (多选题)下列说法中,错误的是( )
A. 任何一条直线都有唯一的斜率
B. 直线的倾斜角越大,它的斜率就越大
C. 任何一条直线都有唯一的倾斜角
D. 若两直线的倾斜角相等,则它们的斜率也一定相等
2. 已知直线的倾斜角为,则下列结论中正确的是( )
A. B. C. D.
3. 若直线的倾斜角是斜率为的直线的倾斜角的2倍,则的斜率( )
A. 1 B. C. D.
4. 若直线的一个方向向量为,则它的倾斜角为( )
A. 300 B. 600 C. 1200 D. 1500
5. 已知直线x=1,则其斜率为( )
A. 不存在 B. 0 C. 1 D. 2
6. 已知点A(-1,3),点B(,),则直线AB的倾斜角为( )
A. 300 B. 450 C. 1200 D. 1350
7. 已知直线的斜率为k,倾斜角为,若,则k的取值范围( )
A. (-1,1) B. (-∞,-1)∪(1,+∞) C. [-1,1] D. (-∞,-1]∪[1,+∞)
8. 设直线的斜率为k,且,则直线的倾斜角为的取值范围( )
A. B. C. D.
9. 已知直线的斜率为k,倾斜角为,则“”是“k≤1”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
答案
ABD 2.D 3. B 4. C 5.A 6. C 7. B 8.D 9.A
2.1.2 两条直线平行和垂直的判定
1. 若A(-1,3),B(4,8),C(5,x),且A,B,C三点共线,则x=( )
A. -2 B.5 C.10 D. 12
2. 已知直线经过点A(-1,2),B(-1,4),直线经过点P(2,1),Q(x,6),且,则x=( )
A. 2 B. -2 C. 4 D. 1
3. 若直线的倾斜角为1350,直线经过点A(2,-1),B(-3,4),则直线与的位置关系( )
A. 垂直 B. 平行 C. 重合 D. 平行或重合
4. 若过点P(3,2m)和点Q(-m,2)的直线与方向向量为的直线平行,则实数m的值为( )
A. B. C. 2 D. -2
5. 已知直线,的斜率与方程的两个根分别相等,则( )
A. B. C. 与相交但不垂直 D. 与的位置关系不确定
6. 过点与B(7,0)的直线与过点(2,1),(3,k+1)的直线和两坐标轴围成的四边形内接于一个圆,则实数k等于( )
A. -3 B. 3 C. -6 D. 6
7. 已知,不重合,直线经过点A(-2,m)和点B(m,4),直线的斜率为-2,直线的斜率为,若,则m+n的值为__________
答案
C 2. A 3. D 4. B 5. C 6. B 7. -10
学习目标
在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素;
理解直线的倾斜角和斜率的概念,经历用代数方法刻画直线斜率的过程,掌握过两点直线斜率的计算公式;
能根据斜率判断两条直线平行或垂直;
掌握用代数方法研究直线的相关问题,体会数形结合的数学思想方法,发展数学思维,落实直观想象和数学运算的核心素养。
知识清单
直线的倾斜角和斜率
倾斜角定义:当直线与轴________时,以轴为基准,轴______与直线_______方向之间所成的_______叫做直线的_______。
当直线与轴_____或____时,它的倾斜角为_____;当直线与轴_____时,它的倾斜角为_____。直线倾斜角的取值范围是_________。
问:不同直线的倾斜角一定不相同吗?
斜率定义:若直线的倾斜角为,则______时,直线的斜率______;当______时,直线的斜率______。
斜率与倾斜角的对应关系
图示
倾斜角
斜率 k
问:直线的斜率一定随着倾斜角的增大而增大吗?
已知直线经过两点,若,则直线的斜率_______;若,则直线的斜率_______;
注:若已知两点的横坐标中含有参数,则需要对参数进行________,分类的依据就是____________________。
直线的方向向量与斜率的关系
当直线的斜率k存在时,直线的一个方向向量为_________;
当直线的一个方向向量为时,直线的斜率k=_________。
两条直线平行的判定
类型 斜率存在
前提 条件
对应 关系
图示
注:若重合,则或的斜率不存在。
问:(1)若两直线(不重合)平行,则两直线的倾斜角一定相等吗?反之呢?
若两直线(不重合)的斜率相等,则两直线平行,正确吗?反之呢?
两条直线垂直的判定
图示
对应关系
问:设直线的斜率为,直线垂直于直线,则直线的斜率为,此结论正确吗?
自我检测
2.1.1 倾斜角与斜率
1. (多选题)下列说法中,错误的是( )
A. 任何一条直线都有唯一的斜率
B. 直线的倾斜角越大,它的斜率就越大
C. 任何一条直线都有唯一的倾斜角
D. 若两直线的倾斜角相等,则它们的斜率也一定相等
2. 已知直线的倾斜角为,则下列结论中正确的是( )
A. B. C. D.
3. 若直线的倾斜角是斜率为的直线的倾斜角的2倍,则的斜率( )
A. 1 B. C. D.
4. 若直线的一个方向向量为,则它的倾斜角为( )
A. 300 B. 600 C. 1200 D. 1500
5. 已知直线x=1,则其斜率为( )
A. 不存在 B. 0 C. 1 D. 2
6. 已知点A(-1,3),点B(,),则直线AB的倾斜角为( )
A. 300 B. 450 C. 1200 D. 1350
7. 已知直线的斜率为k,倾斜角为,若,则k的取值范围( )
A. (-1,1) B. (-∞,-1)∪(1,+∞) C. [-1,1] D. (-∞,-1]∪[1,+∞)
8. 设直线的斜率为k,且,则直线的倾斜角为的取值范围( )
A. B. C. D.
9. 已知直线的斜率为k,倾斜角为,则“”是“k≤1”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
答案
ABD 2.D 3. B 4. C 5.A 6. C 7. B 8.D 9.A
2.1.2 两条直线平行和垂直的判定
1. 若A(-1,3),B(4,8),C(5,x),且A,B,C三点共线,则x=( )
A. -2 B.5 C.10 D. 12
2. 已知直线经过点A(-1,2),B(-1,4),直线经过点P(2,1),Q(x,6),且,则x=( )
A. 2 B. -2 C. 4 D. 1
3. 若直线的倾斜角为1350,直线经过点A(2,-1),B(-3,4),则直线与的位置关系( )
A. 垂直 B. 平行 C. 重合 D. 平行或重合
4. 若过点P(3,2m)和点Q(-m,2)的直线与方向向量为的直线平行,则实数m的值为( )
A. B. C. 2 D. -2
5. 已知直线,的斜率与方程的两个根分别相等,则( )
A. B. C. 与相交但不垂直 D. 与的位置关系不确定
6. 过点与B(7,0)的直线与过点(2,1),(3,k+1)的直线和两坐标轴围成的四边形内接于一个圆,则实数k等于( )
A. -3 B. 3 C. -6 D. 6
7. 已知,不重合,直线经过点A(-2,m)和点B(m,4),直线的斜率为-2,直线的斜率为,若,则m+n的值为__________
答案
C 2. A 3. D 4. B 5. C 6. B 7. -10
