第三章 数据的分析章末复习题(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
第三章 数据的分析
章末复习
考点1 平均数、众数、中位数
1.一组数据4,5,6,a,b的平均数为5,则a,b的平均数为( )
A.4 B.5 C.8 D.10
2.(多选)小莹所在班级 10名同学的身高数据如表所示.
编号 1 2 3 4 5 6 7 8 9 10
身高(cm) 165 158 168 162 174 168 162 165 168 170
下列统计量中,能够描述这组数据集中趋势的是( )
A.平均数 B.方差 C.众数 D.中位数
3.如图是某品牌运动服的S号,M号,L号,XL号的销售情况统计图,则厂家应生产最多的型号为( )
A. S号 B. M号 C. L号 D. XL号
4.小红在“养成阅读习惯,快乐阅读,健康成长”读书大赛活动中,随机调查了本校初二年级 20名同学,在近5个月内每人阅读课外书的数量,数据如下表所示:
人数 3 4 8 5
课外书数量(本) 12 13 15 18
则阅读课外书数量的中位数和众数分别是( )
A.13,15 B.14,15 C.13,18 D.15,15
5.为深入落实“立德树人”的根本任务,坚持德、智、体、美、劳全面发展,某学校积极推进学生综合素质评价改革,某同学在本学期德智体美劳的评价得分如图所示,则该同学五项评价得分的众数,中位数,平均数分别为( )
A.8,8,8 B.7,7,7.8 C.8,8,8.6 D.8,8,8.4
6.五名同学捐款数分别是5,3,6,5,10(单位:元),捐10元的同学后来又追加了10元.追加后的5个数据与之前的5个数据相比,集中趋势相同的是( )
A.只有平均数 B.只有中位数 C.只有众数 D.中位数和众数
7.小明参加“建团百年,我为团旗添光彩”主题演讲比赛,其演讲形象、内容、效果三项分别是9分、8分、8分.若将三项得分依次按3:4:3的比例确定最终成绩,则小明的最终比赛成绩为__________分.
8.某校九(1)班 10名同学进行“引体向上”训练,将他们做的次数进行统计,制成下表,则这10名同学做的次数组成的一组数据中,中位数为__________.
次数 4 5 6 7 8
人数 2 3 2 2 1
9.为了加强心理健康教育,某校组织七年级(1)(2)两班学生进行了心理健康常识测试(分数为整数,满分为 10分),已知两班学生人数相同,根据测试成绩绘制了如下所示的统计图.
(1)求(2)班学生中测试成绩为10分的人数;
(2)请确定下表中a,b,c的值(只要求写出求a的计算过程);
统计量 平均数 众数 中位数 方差
(1)班 8 8 c 1.16
(2)班 a b 8 1.56
(3)从上表中选择合适的统计量,说明哪个班的成绩更均匀.
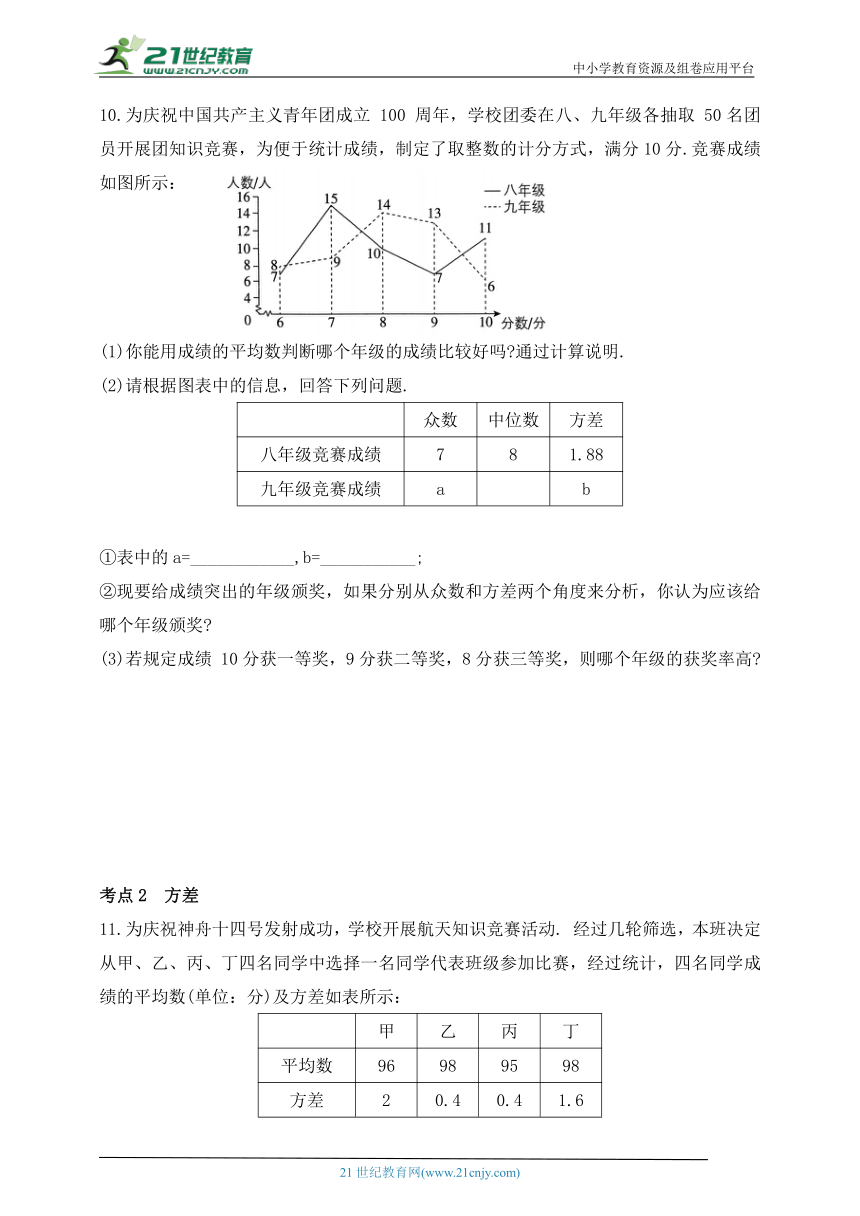
10.为庆祝中国共产主义青年团成立 100 周年,学校团委在八、九年级各抽取 50名团员开展团知识竞赛,为便于统计成绩,制定了取整数的计分方式,满分10分.竞赛成绩如图所示:
(1)你能用成绩的平均数判断哪个年级的成绩比较好吗 通过计算说明.
(2)请根据图表中的信息,回答下列问题.
众数 中位数 方差
八年级竞赛成绩 7 8 1.88
九年级竞赛成绩 a b
①表中的a=____________,b=___________;
②现要给成绩突出的年级颁奖,如果分别从众数和方差两个角度来分析,你认为应该给哪个年级颁奖
(3)若规定成绩 10分获一等奖,9分获二等奖,8分获三等奖,则哪个年级的获奖率高
考点2 方差
11.为庆祝神舟十四号发射成功,学校开展航天知识竞赛活动. 经过几轮筛选,本班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛,经过统计,四名同学成绩的平均数(单位:分)及方差如表所示:
甲 乙 丙 丁
平均数 96 98 95 98
方差 2 0.4 0.4 1.6
如果要选一名成绩好且状态稳定的同学参赛,那么应该选择( )
A.甲 B.乙 C.丙 D.丁
12.某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如图所示,甲、乙两选手成绩的方差分别记为 则 (填“>”“<”或“=”)
参考答案
1. B【解析】因为一组数据4,5,6,a,b的平均数为5,所以4+5+6+a+b=5×5,所以a+b=10,所以a,b的平均数为10÷2=5,故选 B.
2. ACD【解析】由定义知,平均数、中位数、众数都可以描述数据的集中趋势,故选ACD.
3. B 【解析】∵32%>26%>24%>18%,∴厂家应生产最多的型号为 M号.故选 B.
4. D【解析】中位数为第10个和第11个数据的平均数,即 (本),阅读课外书数量为15本的人数最多,所以众数为15.故选 D.
5. D【解析】该同学五项评价得分分别为7,8,8,9,10,出现次数最多的数是8,所以众数为8;位于中间位置的数是8,所以中位数是8;平均数为 故选D.
6. D【解析】根据题意知,追加前的5个数据的平均数是5.8,中位数是5,众数是5;追加后5个数据的平均数是7.8,中位数是5,众数为 5,所以集中趋势相同的是中位数和众数. 故选 D.
7.8.3 【解析】根据题意得 8.3(分),故小明的最终比赛成绩为8.3分.
故答案为8.3.
8.5.5【解析】10名同学做的次数组成的一组数据中,中位数是 故答案为5.5.
9.【解】(1)由题意知,(1)班和(2)班学生人数相等,∴(2)班学生有5+10+19+12+4=50(人),
∴(2)班学生中测试成绩为10分的人数为50×(1-28%-22%-24%-14%)=6.
(2)由题意知, 22%×8+50×24%×7+50×14%×6)= 8;b=9;c=8.
(3)根据方差越小,数据分布越均匀可知(1)班成绩更均匀.
10.【解】(1)不能.理由如下:由题意得八年级成绩的平均数是(6×7+7×15+8×10+9×7+10×11)÷50=8(分),九年级成绩的平均数是(6×8+7×9+8×14+9×13+10×6)÷50=8(分),故用平均数无法判断哪个年级的成绩比较好.
(2)①九年级竞赛成绩中8分出现的次数最多,故众数 a=8.九年级竞赛成绩的方差为 8) +13×(9-8) +6×(10-8) ]=1.56,即b=1.56.故答案为8,1.56.
②如果从众数角度看,八年级的众数为7分,九年级的众数为8分,所以应该给九年级颁奖;如果从方差角度看,八年级的方差为1.88,九年级的方差为1.56,又因为两个年级的平均数相同,九年级的成绩波动小,所以应该给九年级颁奖.综上所述,应该给九年级颁奖.
(3)八年级的获奖率为(10+7+11)÷50×100%=56%,九年级的获奖率为(14+13+6)÷50×100%=66%.∵66%>56%,∴九年级的获奖率高.
11. B【解析】∵乙、丁同学成绩的平均数比甲、丙同学的平均数大,∴应从乙和丁同学
中选.∵乙同学成绩的方差比丁同学的小,∴乙同学的成绩较好且状态稳定,故应选择乙同学.故选 B.
12.>【解析】由题图可知甲选手成绩与乙选手相比波动较大,故 故答案为>.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章 数据的分析
章末复习
考点1 平均数、众数、中位数
1.一组数据4,5,6,a,b的平均数为5,则a,b的平均数为( )
A.4 B.5 C.8 D.10
2.(多选)小莹所在班级 10名同学的身高数据如表所示.
编号 1 2 3 4 5 6 7 8 9 10
身高(cm) 165 158 168 162 174 168 162 165 168 170
下列统计量中,能够描述这组数据集中趋势的是( )
A.平均数 B.方差 C.众数 D.中位数
3.如图是某品牌运动服的S号,M号,L号,XL号的销售情况统计图,则厂家应生产最多的型号为( )
A. S号 B. M号 C. L号 D. XL号
4.小红在“养成阅读习惯,快乐阅读,健康成长”读书大赛活动中,随机调查了本校初二年级 20名同学,在近5个月内每人阅读课外书的数量,数据如下表所示:
人数 3 4 8 5
课外书数量(本) 12 13 15 18
则阅读课外书数量的中位数和众数分别是( )
A.13,15 B.14,15 C.13,18 D.15,15
5.为深入落实“立德树人”的根本任务,坚持德、智、体、美、劳全面发展,某学校积极推进学生综合素质评价改革,某同学在本学期德智体美劳的评价得分如图所示,则该同学五项评价得分的众数,中位数,平均数分别为( )
A.8,8,8 B.7,7,7.8 C.8,8,8.6 D.8,8,8.4
6.五名同学捐款数分别是5,3,6,5,10(单位:元),捐10元的同学后来又追加了10元.追加后的5个数据与之前的5个数据相比,集中趋势相同的是( )
A.只有平均数 B.只有中位数 C.只有众数 D.中位数和众数
7.小明参加“建团百年,我为团旗添光彩”主题演讲比赛,其演讲形象、内容、效果三项分别是9分、8分、8分.若将三项得分依次按3:4:3的比例确定最终成绩,则小明的最终比赛成绩为__________分.
8.某校九(1)班 10名同学进行“引体向上”训练,将他们做的次数进行统计,制成下表,则这10名同学做的次数组成的一组数据中,中位数为__________.
次数 4 5 6 7 8
人数 2 3 2 2 1
9.为了加强心理健康教育,某校组织七年级(1)(2)两班学生进行了心理健康常识测试(分数为整数,满分为 10分),已知两班学生人数相同,根据测试成绩绘制了如下所示的统计图.
(1)求(2)班学生中测试成绩为10分的人数;
(2)请确定下表中a,b,c的值(只要求写出求a的计算过程);
统计量 平均数 众数 中位数 方差
(1)班 8 8 c 1.16
(2)班 a b 8 1.56
(3)从上表中选择合适的统计量,说明哪个班的成绩更均匀.
10.为庆祝中国共产主义青年团成立 100 周年,学校团委在八、九年级各抽取 50名团员开展团知识竞赛,为便于统计成绩,制定了取整数的计分方式,满分10分.竞赛成绩如图所示:
(1)你能用成绩的平均数判断哪个年级的成绩比较好吗 通过计算说明.
(2)请根据图表中的信息,回答下列问题.
众数 中位数 方差
八年级竞赛成绩 7 8 1.88
九年级竞赛成绩 a b
①表中的a=____________,b=___________;
②现要给成绩突出的年级颁奖,如果分别从众数和方差两个角度来分析,你认为应该给哪个年级颁奖
(3)若规定成绩 10分获一等奖,9分获二等奖,8分获三等奖,则哪个年级的获奖率高
考点2 方差
11.为庆祝神舟十四号发射成功,学校开展航天知识竞赛活动. 经过几轮筛选,本班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛,经过统计,四名同学成绩的平均数(单位:分)及方差如表所示:
甲 乙 丙 丁
平均数 96 98 95 98
方差 2 0.4 0.4 1.6
如果要选一名成绩好且状态稳定的同学参赛,那么应该选择( )
A.甲 B.乙 C.丙 D.丁
12.某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如图所示,甲、乙两选手成绩的方差分别记为 则 (填“>”“<”或“=”)
参考答案
1. B【解析】因为一组数据4,5,6,a,b的平均数为5,所以4+5+6+a+b=5×5,所以a+b=10,所以a,b的平均数为10÷2=5,故选 B.
2. ACD【解析】由定义知,平均数、中位数、众数都可以描述数据的集中趋势,故选ACD.
3. B 【解析】∵32%>26%>24%>18%,∴厂家应生产最多的型号为 M号.故选 B.
4. D【解析】中位数为第10个和第11个数据的平均数,即 (本),阅读课外书数量为15本的人数最多,所以众数为15.故选 D.
5. D【解析】该同学五项评价得分分别为7,8,8,9,10,出现次数最多的数是8,所以众数为8;位于中间位置的数是8,所以中位数是8;平均数为 故选D.
6. D【解析】根据题意知,追加前的5个数据的平均数是5.8,中位数是5,众数是5;追加后5个数据的平均数是7.8,中位数是5,众数为 5,所以集中趋势相同的是中位数和众数. 故选 D.
7.8.3 【解析】根据题意得 8.3(分),故小明的最终比赛成绩为8.3分.
故答案为8.3.
8.5.5【解析】10名同学做的次数组成的一组数据中,中位数是 故答案为5.5.
9.【解】(1)由题意知,(1)班和(2)班学生人数相等,∴(2)班学生有5+10+19+12+4=50(人),
∴(2)班学生中测试成绩为10分的人数为50×(1-28%-22%-24%-14%)=6.
(2)由题意知, 22%×8+50×24%×7+50×14%×6)= 8;b=9;c=8.
(3)根据方差越小,数据分布越均匀可知(1)班成绩更均匀.
10.【解】(1)不能.理由如下:由题意得八年级成绩的平均数是(6×7+7×15+8×10+9×7+10×11)÷50=8(分),九年级成绩的平均数是(6×8+7×9+8×14+9×13+10×6)÷50=8(分),故用平均数无法判断哪个年级的成绩比较好.
(2)①九年级竞赛成绩中8分出现的次数最多,故众数 a=8.九年级竞赛成绩的方差为 8) +13×(9-8) +6×(10-8) ]=1.56,即b=1.56.故答案为8,1.56.
②如果从众数角度看,八年级的众数为7分,九年级的众数为8分,所以应该给九年级颁奖;如果从方差角度看,八年级的方差为1.88,九年级的方差为1.56,又因为两个年级的平均数相同,九年级的成绩波动小,所以应该给九年级颁奖.综上所述,应该给九年级颁奖.
(3)八年级的获奖率为(10+7+11)÷50×100%=56%,九年级的获奖率为(14+13+6)÷50×100%=66%.∵66%>56%,∴九年级的获奖率高.
11. B【解析】∵乙、丁同学成绩的平均数比甲、丙同学的平均数大,∴应从乙和丁同学
中选.∵乙同学成绩的方差比丁同学的小,∴乙同学的成绩较好且状态稳定,故应选择乙同学.故选 B.
12.>【解析】由题图可知甲选手成绩与乙选手相比波动较大,故 故答案为>.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
