21.1 二次根式-华师大版数学九年级上册课件(共22张PPT)
文档属性
| 名称 | 21.1 二次根式-华师大版数学九年级上册课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 876.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-31 22:58:43 | ||
图片预览








文档简介
(共22张PPT)
第21章 二次根式
21.1 二次根式
学习目标
1. 理解二次根式的概念;
2. 会确定二次根式有意义时字母的取值范围; (重点)
3. 探索二次根式的性质; (难点)
4. 运用二次根式的性质进行化简计算. (难点)
导入新课
问题2 什么是一个数的算术平方根?如何表示?
正数的正的平方根叫做它的算术平方根.
问题1 什么叫做一个数的平方根?如何表示?
一般地,若一个数的平方等于 a,则这个数就叫做 a 的平方根.
0 的算术平方根是0.
a 的平方根是 .
用 (a≥0)表示.
正数有两个平方根且互为相反数;
0有一个平方根就是 0;
负数没有平方根.
问题3 平方根的性质:
正数和 0 都有算术平方根;
负数没有算术平方根.
问题4 所有实数都有算术平方根吗?
回顾
当a是正数时, 表示a的算术平方根,即正数a的正的平方根.
当a是零时, 等于0,它表示零的平方根,也叫做零的算术平方根.
当a是负数时,没有意义.
2. 二次根式实质上是非负数的算术平方根.
3. a 既可以是一个数,也可以是一个式子.
请你凭着自己已有的知识,说说对二次根式 的认识!
1. 既可表示开方运算,也可表示运算的结果.
概括归纳
(a>0)表示非负数a的算术平方根,也就是说(a≥0) 是一个非负数,它的平方等于a,即有:
(1)≥0 (a≥0);
(2)() = a(a≥0).
形如(a≥0)的式子叫做二次根式.
注意:在 中,a的取值必须满足a≥0,即二次根式的被开方数必须是非负数.
典例精析
x是怎样的实数时,二次根式 有意义
分析:要使二次根式有意义,被开方数必须是非负数.
解:被开方数≥0,即x≥1.
所以,当x≥1时,二次根式有意义.
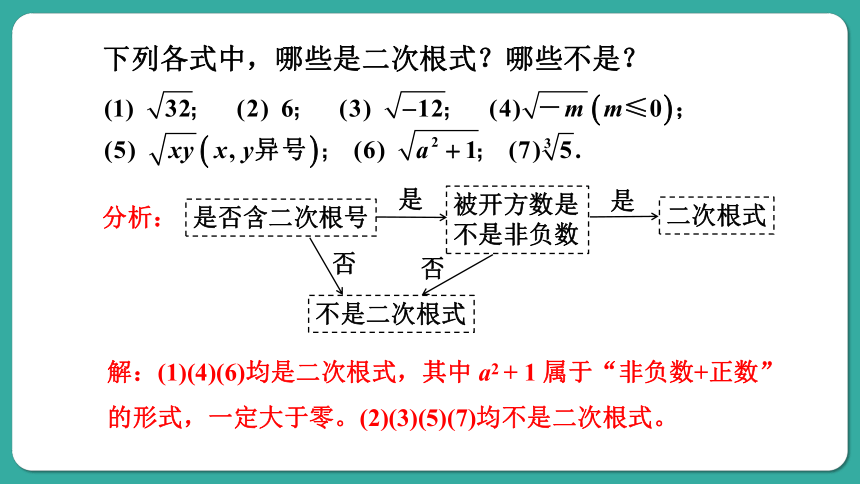
下列各式中,哪些是二次根式?哪些不是?
解:(1)(4)(6)均是二次根式,其中 a2 + 1 属于“非负数+正数”的形式,一定大于零。(2)(3)(5)(7)均不是二次根式。
是否含二次根号
被开方数是不是非负数
二次根式
不是二次根式
是
是
否
否
分析:
思考
等于什么
我们不妨取a的一些值,如2、-2、3、-3 等,
分别计算对应的的值,看看有什么规律:
==2;
==2;
==3;
==3;
这里a的取值有没有限制?取a的一些值,分别计算的值. 从中你能发现什么
这里a的取值没有限制,因为a 是非负数,所以a既可以取正数或0,也可以取负数如当a=3时, ==3;当a=0时, =0;当a=-3时, ==3……从中可以发现:当a取任意实数时,=|a|.
概括归纳
当a≥0时, =a;
当a<0时, =-a.
这是二次根式的又一重要性质. 如果二次根式的被开方数是一个完全平方数,运用这个性质,可以将它“开方”出来,从而达到化简的目的。
知识要点
=∣a∣
2.从取值范围来看,
a≥0
a 取任何实数
1.从运算顺序来看,
先开方,后平方
先平方,后开方
3.从运算结果来看:
=a
a (a≥0)
-a (a<0)
=
练一练
化简
解:
解:由 x-1≥0,得
x≥1
1. 当 x 取何值时, 二次根式有意义
当 x≥1 时, 在实数范围内有意义.
试求当 x = 5 时,二次根式 的值.
当 x = 5 时,
思考:当 x 是怎样的实数时, 在实数范围内有意义?
x为全体实数.
当堂练习
1.计算:
(1)() ; (2) () ; (3) ; (4)
=8
=9
=
=9
=10
2. x是怎样的实数时,下列二次根式有意义
(1);
∵有意义; ∴x+3≥0 ,∴ x≥-3,
∴当x≥-3时,二次根式有意义.
(2);
∵有意义; ∴ ≥0 ,∴ x≥,
∴当x≥时,二次根式有意义.
(3) ;
∵有意义; ∴ >0 ,∴ x>0,
∴当x>0时,二次根式有意义.
(4) ;
∵有意义; ∴ >0 ,∴ x<1,
∴当x<1时,二次根式有意义.
3. () 与是一样的吗?说说你的理由,并与同学交流。
() 与不一样。理由如下:
() 中a只能取非负数,但中a可以取任意实数;
() 表示数a的算术平方根的平方,而表示数a的平方的算术平方根。
5.(1)若 ,则 a - b + c =___ ;
解:(1)由题意可知 a - 2 = 0,b - 3 = 0,c - 4 = 0,
解得 a = 2,b = 3,c = 4.
所以 a - b + c = 2 - 3 + 4 = 3.
(2)由题意知 1 - x≥0,且 x - 1≥0,联立解得 x = 1.
从而知 y = 2022,
所以 x + 2y = 1+2×2022 = 4045.
3
课堂小结
二次根式
定义
性质
(a≥0)
(即 表示一个非负数)
谢谢观看
谢谢观看
第21章 二次根式
21.1 二次根式
学习目标
1. 理解二次根式的概念;
2. 会确定二次根式有意义时字母的取值范围; (重点)
3. 探索二次根式的性质; (难点)
4. 运用二次根式的性质进行化简计算. (难点)
导入新课
问题2 什么是一个数的算术平方根?如何表示?
正数的正的平方根叫做它的算术平方根.
问题1 什么叫做一个数的平方根?如何表示?
一般地,若一个数的平方等于 a,则这个数就叫做 a 的平方根.
0 的算术平方根是0.
a 的平方根是 .
用 (a≥0)表示.
正数有两个平方根且互为相反数;
0有一个平方根就是 0;
负数没有平方根.
问题3 平方根的性质:
正数和 0 都有算术平方根;
负数没有算术平方根.
问题4 所有实数都有算术平方根吗?
回顾
当a是正数时, 表示a的算术平方根,即正数a的正的平方根.
当a是零时, 等于0,它表示零的平方根,也叫做零的算术平方根.
当a是负数时,没有意义.
2. 二次根式实质上是非负数的算术平方根.
3. a 既可以是一个数,也可以是一个式子.
请你凭着自己已有的知识,说说对二次根式 的认识!
1. 既可表示开方运算,也可表示运算的结果.
概括归纳
(a>0)表示非负数a的算术平方根,也就是说(a≥0) 是一个非负数,它的平方等于a,即有:
(1)≥0 (a≥0);
(2)() = a(a≥0).
形如(a≥0)的式子叫做二次根式.
注意:在 中,a的取值必须满足a≥0,即二次根式的被开方数必须是非负数.
典例精析
x是怎样的实数时,二次根式 有意义
分析:要使二次根式有意义,被开方数必须是非负数.
解:被开方数≥0,即x≥1.
所以,当x≥1时,二次根式有意义.
下列各式中,哪些是二次根式?哪些不是?
解:(1)(4)(6)均是二次根式,其中 a2 + 1 属于“非负数+正数”的形式,一定大于零。(2)(3)(5)(7)均不是二次根式。
是否含二次根号
被开方数是不是非负数
二次根式
不是二次根式
是
是
否
否
分析:
思考
等于什么
我们不妨取a的一些值,如2、-2、3、-3 等,
分别计算对应的的值,看看有什么规律:
==2;
==2;
==3;
==3;
这里a的取值有没有限制?取a的一些值,分别计算的值. 从中你能发现什么
这里a的取值没有限制,因为a 是非负数,所以a既可以取正数或0,也可以取负数如当a=3时, ==3;当a=0时, =0;当a=-3时, ==3……从中可以发现:当a取任意实数时,=|a|.
概括归纳
当a≥0时, =a;
当a<0时, =-a.
这是二次根式的又一重要性质. 如果二次根式的被开方数是一个完全平方数,运用这个性质,可以将它“开方”出来,从而达到化简的目的。
知识要点
=∣a∣
2.从取值范围来看,
a≥0
a 取任何实数
1.从运算顺序来看,
先开方,后平方
先平方,后开方
3.从运算结果来看:
=a
a (a≥0)
-a (a<0)
=
练一练
化简
解:
解:由 x-1≥0,得
x≥1
1. 当 x 取何值时, 二次根式有意义
当 x≥1 时, 在实数范围内有意义.
试求当 x = 5 时,二次根式 的值.
当 x = 5 时,
思考:当 x 是怎样的实数时, 在实数范围内有意义?
x为全体实数.
当堂练习
1.计算:
(1)() ; (2) () ; (3) ; (4)
=8
=9
=
=9
=10
2. x是怎样的实数时,下列二次根式有意义
(1);
∵有意义; ∴x+3≥0 ,∴ x≥-3,
∴当x≥-3时,二次根式有意义.
(2);
∵有意义; ∴ ≥0 ,∴ x≥,
∴当x≥时,二次根式有意义.
(3) ;
∵有意义; ∴ >0 ,∴ x>0,
∴当x>0时,二次根式有意义.
(4) ;
∵有意义; ∴ >0 ,∴ x<1,
∴当x<1时,二次根式有意义.
3. () 与是一样的吗?说说你的理由,并与同学交流。
() 与不一样。理由如下:
() 中a只能取非负数,但中a可以取任意实数;
() 表示数a的算术平方根的平方,而表示数a的平方的算术平方根。
5.(1)若 ,则 a - b + c =___ ;
解:(1)由题意可知 a - 2 = 0,b - 3 = 0,c - 4 = 0,
解得 a = 2,b = 3,c = 4.
所以 a - b + c = 2 - 3 + 4 = 3.
(2)由题意知 1 - x≥0,且 x - 1≥0,联立解得 x = 1.
从而知 y = 2022,
所以 x + 2y = 1+2×2022 = 4045.
3
课堂小结
二次根式
定义
性质
(a≥0)
(即 表示一个非负数)
谢谢观看
谢谢观看
