2023-2024学年华师大版数学八年级上册11.2 实数 课件(共24张PPT)
文档属性
| 名称 | 2023-2024学年华师大版数学八年级上册11.2 实数 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-01 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
11.2 实数
做一 做
(1)用计算器求
(2)利用平方运算验算(1)中所得的结果
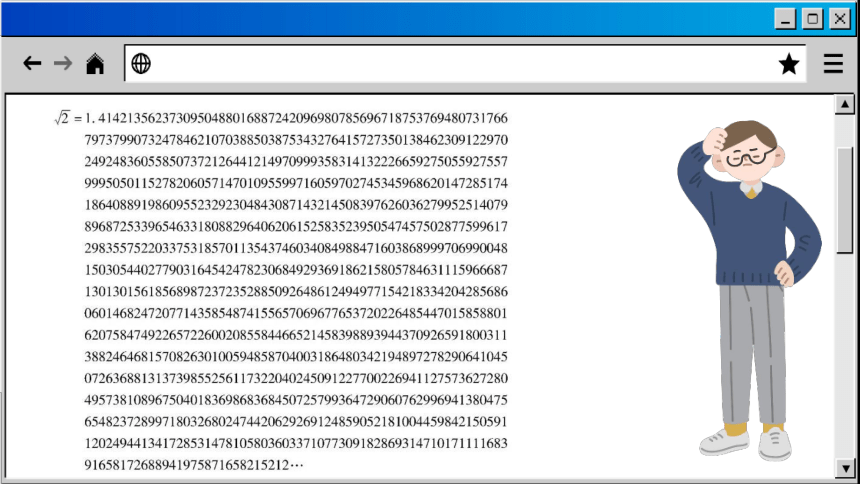
用计算器求显示结果为414 213562. 再用计算器计算 1.414 213 562 的平方,结果是 1.999 999 999,不是 2。这说明计算器求得的只是的近似值用计算机计算 ,你可能会大吃一惊
在数学上已经证明,没有一个有理数的平方等于 2也就是说,不是一个有理数.
那么,是怎样的数呢
我们知道,有理数包括整数和分数,而任何一个分数写成小数的形式,必定是有限小数或者无限循环小数,例如:
=0.25 =0.6=0.6666666666……
= 0. 142 857 =0.142 857 142 857...
不是个有理数,实际上,它是一个无限不循环小数.
类似地,、圆周率π等都不是有理数,它们都是无限不循环小数.
概括
无限不循环小数叫做无理数
上面所提到的、都是无理数。
有理数和无理数统称实数。
试一试
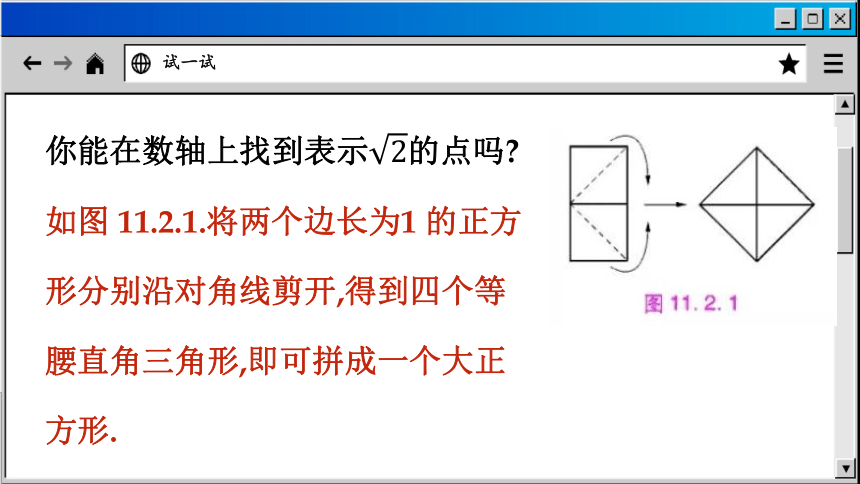
你能在数轴上找到表示的点吗
如图 11.2.1.将两个边长为1 的正方形分别沿对角线剪开,得到四个等腰直角三角形,即可拼成一个大正方形.
容易知道,这个大正方形的面积是 2所以大正方形的边长为
2.这就是说,边长为1的正方形的对角线长是2.
利用这个事实,我们容易在数轴上画出表示 2 的点,如图11.2.2 所示
概括
数学上可以证明,数轴上的每一点必定表示一个实数;反过来每一个实数(有理数或无理数)都可以用数轴上的一个点来表示。
换句话说,实数与数轴上的点一一对应这是数集从有理数集扩充到实数集的一大进步
在七年级上学期第2章学过的有关有理数的相反数和绝对值等概念、大小比较法则、运算法则以及运算律对于实数也适用.
从有理数扩充到实数以后,正数总可以开方。在实数范围内,任意一个正数有两个平方根,它们互为相反数
0的平方根是0
负数没有平方根任意一个实数有且仅有一个立方根.
涉及无理数的大小比较和运算,通常可以取它们的近似值来进行。
例题1
试比较+ 与π的大小。
解:用计算器求得:+ ≈3.146 264 37
而π≈3.141592654
因此: + >π
例题2
计算:(精确到0.01)
≈0.167-1.414=-1.247
于是 ≈1.247
≈1.571-1.247
=0.324≈0.32
注:由于 所以
=
原式=
由此算式,可直接将数据输入计算器进行计算
1.下列说法是否正确 为什么
(1) 两个整教相除,如果永远都除不尽,那么结果一定是一个无理数
(2)任意一个无理数的绝对值都是正数
2.计算:2+3.(精确到0.01)
3.比较下列各对数的大小:
(1)2和3 (2)-和-
1.完成下列表格
2.比较下列各对数的大小
(1)与 (2)-与-
< - < -
3.计算:+.(精确到0.01)
4.对于无理数试解答下列问题
(1)在数轴上位于哪两个相邻的整数之间
(2)借助计算器找出实数a与b,使a<若取a=2.645,由于b a=0.001,则有b=2.646.
11.2 实数
做一 做
(1)用计算器求
(2)利用平方运算验算(1)中所得的结果
用计算器求显示结果为414 213562. 再用计算器计算 1.414 213 562 的平方,结果是 1.999 999 999,不是 2。这说明计算器求得的只是的近似值用计算机计算 ,你可能会大吃一惊
在数学上已经证明,没有一个有理数的平方等于 2也就是说,不是一个有理数.
那么,是怎样的数呢
我们知道,有理数包括整数和分数,而任何一个分数写成小数的形式,必定是有限小数或者无限循环小数,例如:
=0.25 =0.6=0.6666666666……
= 0. 142 857 =0.142 857 142 857...
不是个有理数,实际上,它是一个无限不循环小数.
类似地,、圆周率π等都不是有理数,它们都是无限不循环小数.
概括
无限不循环小数叫做无理数
上面所提到的、都是无理数。
有理数和无理数统称实数。
试一试
你能在数轴上找到表示的点吗
如图 11.2.1.将两个边长为1 的正方形分别沿对角线剪开,得到四个等腰直角三角形,即可拼成一个大正方形.
容易知道,这个大正方形的面积是 2所以大正方形的边长为
2.这就是说,边长为1的正方形的对角线长是2.
利用这个事实,我们容易在数轴上画出表示 2 的点,如图11.2.2 所示
概括
数学上可以证明,数轴上的每一点必定表示一个实数;反过来每一个实数(有理数或无理数)都可以用数轴上的一个点来表示。
换句话说,实数与数轴上的点一一对应这是数集从有理数集扩充到实数集的一大进步
在七年级上学期第2章学过的有关有理数的相反数和绝对值等概念、大小比较法则、运算法则以及运算律对于实数也适用.
从有理数扩充到实数以后,正数总可以开方。在实数范围内,任意一个正数有两个平方根,它们互为相反数
0的平方根是0
负数没有平方根任意一个实数有且仅有一个立方根.
涉及无理数的大小比较和运算,通常可以取它们的近似值来进行。
例题1
试比较+ 与π的大小。
解:用计算器求得:+ ≈3.146 264 37
而π≈3.141592654
因此: + >π
例题2
计算:(精确到0.01)
≈0.167-1.414=-1.247
于是 ≈1.247
≈1.571-1.247
=0.324≈0.32
注:由于 所以
=
原式=
由此算式,可直接将数据输入计算器进行计算
1.下列说法是否正确 为什么
(1) 两个整教相除,如果永远都除不尽,那么结果一定是一个无理数
(2)任意一个无理数的绝对值都是正数
2.计算:2+3.(精确到0.01)
3.比较下列各对数的大小:
(1)2和3 (2)-和-
1.完成下列表格
2.比较下列各对数的大小
(1)与 (2)-与-
< - < -
3.计算:+.(精确到0.01)
4.对于无理数试解答下列问题
(1)在数轴上位于哪两个相邻的整数之间
(2)借助计算器找出实数a与b,使a<
