2023-2024学年华师大版数学八年级上册课件12.1 幂的运算 课件 (共41张PPT)
文档属性
| 名称 | 2023-2024学年华师大版数学八年级上册课件12.1 幂的运算 课件 (共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-01 00:00:00 | ||
图片预览





文档简介
(共41张PPT)
12.1 幂的运算
1. 同底数幂的乘法
试一试
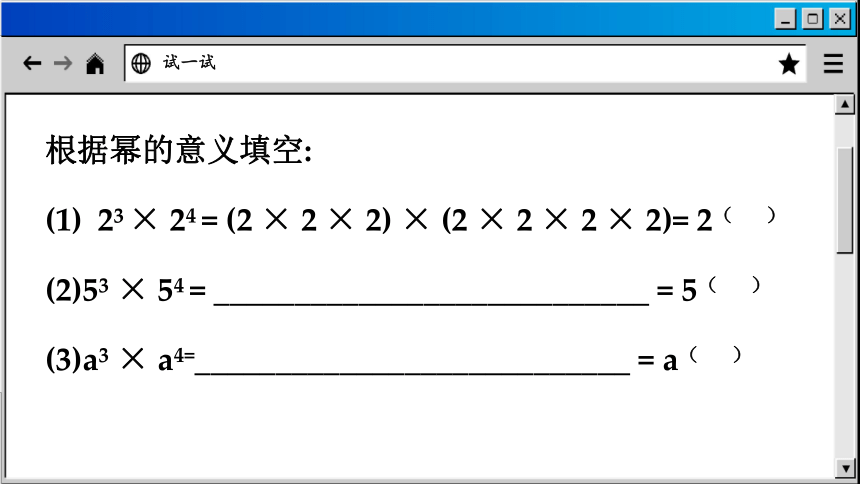
根据幂的意义填空:
23 × 24 = (2 × 2 × 2) × (2 × 2 × 2 × 2)= 2( )
(2)53 × 54 = ___________________________ = 5( )
(3)a3 × a4=___________________________ = a( )
概括
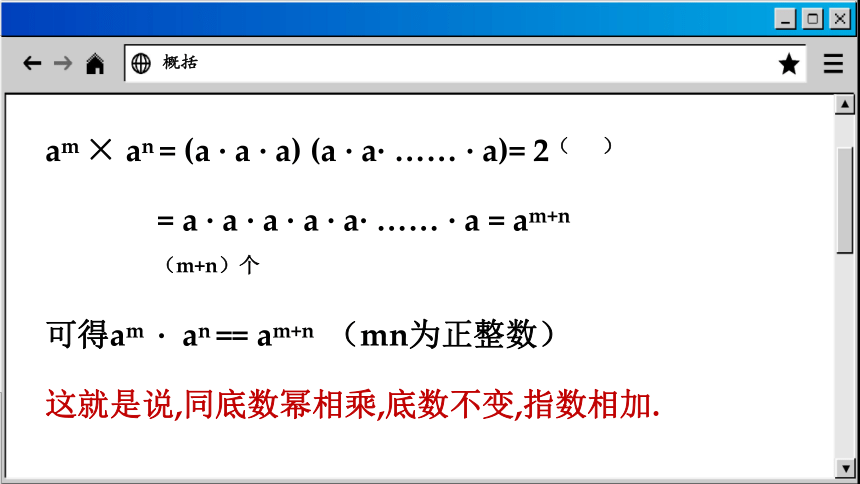
am × an = (a · a · a) (a · a· …… · a)= 2( )
= a · a · a · a · a· …… · a = am+n
(m+n)个
可得am · an == am+n (mn为正整数)
这就是说,同底数幂相乘,底数不变,指数相加.
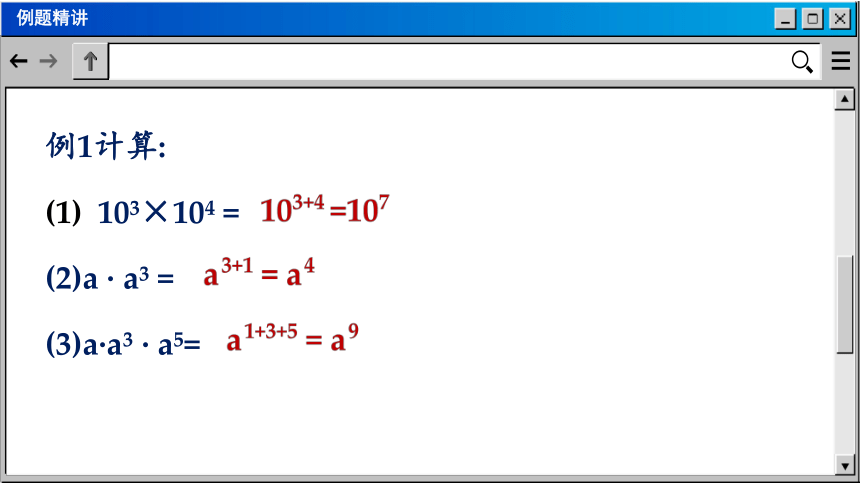
例1计算:
103×104 =
(2)a · a3 =
(3)a·a3 · a5=
1.判断下列计算是否正确,并说明理由:
(l)a·a2=a2 (3)a+a2=a3
(2)a3+a3 =a9 (4)a3+a3=a6
2.计算:
(1) 105×105 (2) a3×a7 (3) x·x5·x7
2.幂的乘方
试一试
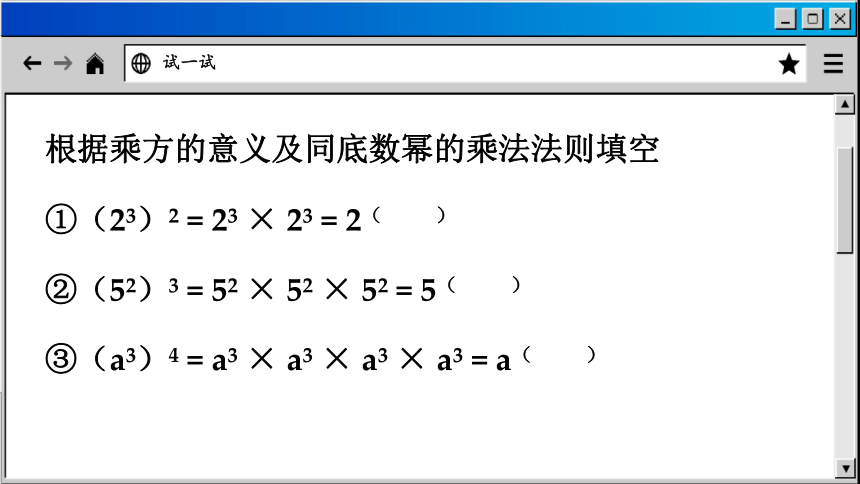
根据乘方的意义及同底数幂的乘法法则填空
①(23)2 = 23 × 23 = 2( )
②(52)3 = 52 × 52 × 52 = 5( )
③(a3)4 = a3 × a3 × a3 × a3 = a( )
概括
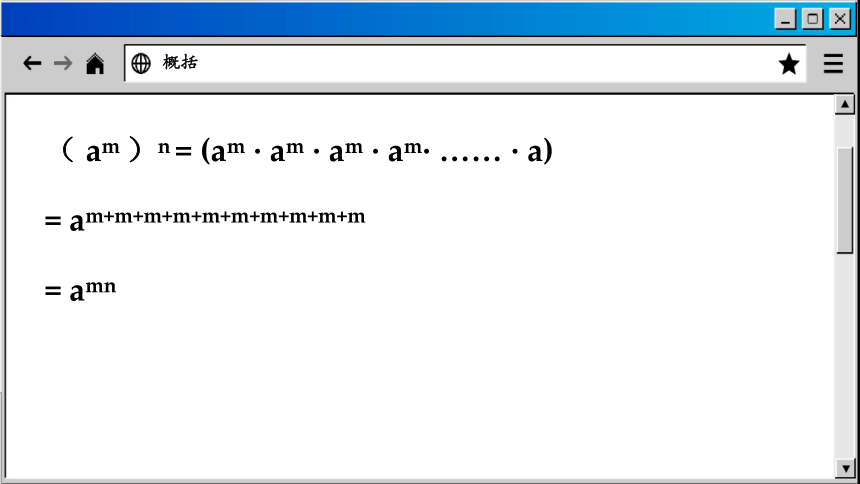
( am )n = (am · am · am · am· …… · a)
= am+m+m+m+m+m+m+m+m+m
= amn
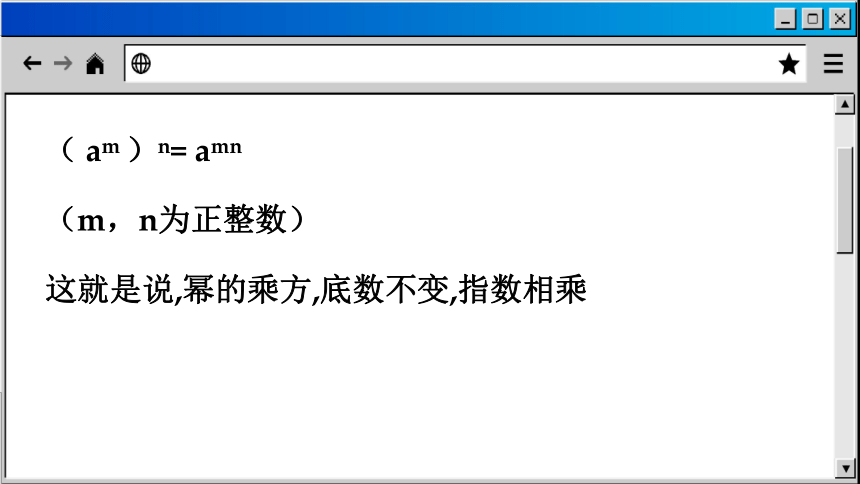
( am )n= amn
(m,n为正整数)
这就是说,幂的乘方,底数不变,指数相乘
例题2
计算
① ( 103 )5 = 103 ×5 = 1015
② ( b5 )4= b5×4 = b20
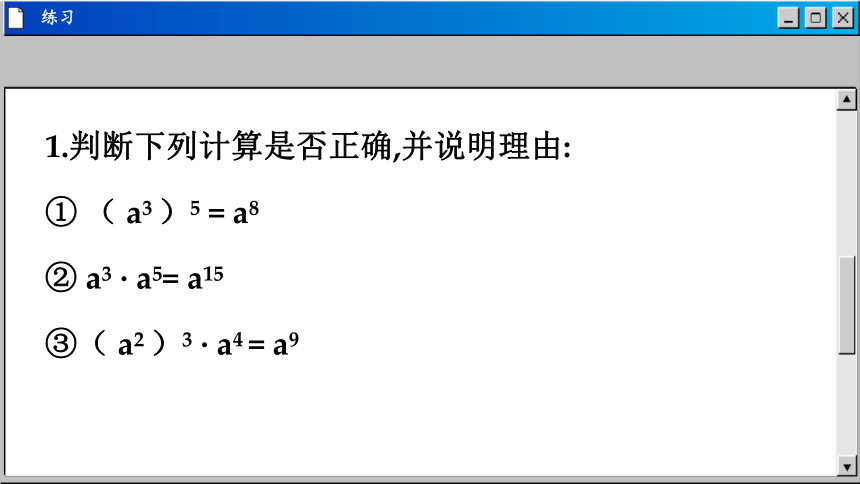
1.判断下列计算是否正确,并说明理由:
① ( a3 )5 = a8
② a3 · a5= a15
③( a2 )3 · a4 = a9
练习
2.计算
①( 22 )2 = ② ( y2 )5 =
③ ( x4 )3 = ④ ( y3 )2 ·( y2) 3 =
练习
3.积的乘方
试一试
根据乘方的意义和乘法运算律填空:
(1)(ab) 2 =(ab)·(ab) (2)(ab) 3
=(aa)·(bb) =__________________
=a( )b( ) =a( )b( )
(3)(ab) 4
=__________________
=a( )b( )
概括
(ab) n
= (ab) · (ab) ·…… · (ab)
= (a · a · a · a) · (b · b · b · b · b)
=a n b n
可得 (ab) n =a n b n (n为正整数)
这就是说,积的乘方,把积的每一个因式分别乘方再把所得的幕相乘。
例题3
例3计算:
(1)(2b) 3 =
(2)(2a 3 ) 2 =
(3)(-a) 3 =
(4)(-3x) 4 =
1.判断下列计算是否正确,并说明理由:
(1)(xy 3) 2 =xy 6
(2)(-2x ) 3 =-6x3
练习 课本第21页
2.计算:
(1)(3a) 2 =
(2)(-3a) 3 =
(3) (ab 2 ) 2 =
(4)(-2×10 3 ) 3 =
练习 课本第21页
4.同底数幂的除法
我们已经知道同底数幂的乘法法则:a m ·a n =a m +n ,那么同底数幂怎么相除呢
用你熟悉的方法计算:
①2 5 ÷2 2 =_____ ②10 7 ÷103 = _____
③ a 7 ÷ a 3 =_________ (a≠0).
由上面的计算,我们发现:
①2 5 ÷2 2 =
②10 7 ÷103 =
③ a 7 ÷ a 3 = (a≠0).
概括
般地设m、n为正整数,m>n,a≠0,有
这就是说,同底数幂相除,底数不变,指数相减
读一读
根据除法的意义推导同底数幂的除法法则前面我们通过一些计算,归纳、探索出同底数幂的除法法则.下面我们根据除法的意义来推导同底数幂的除法法则:
因为除法是乘法的逆运算,计算a m ÷a n (m、n都是正整数,且m>n,a≠0)实际上是要求一个式子,使
a m · ( )=a n
假设这个式子是a(是正整数,待定),即应有
a n · a k = a m
即a n +k = a m
所以n+k=m
得k=m-n
因此,要求的式子应该是a m-n
由同底数幂的乘法法则,可知
a n · a m-n = a n+(m-n) = a m
所以a m-n满足要求,从而有
a m÷a n=a m-n (m、n都是正整数,且m>n,a≠0)
例题4
计算
思考 你能用(a+b)的幂表示 (a+b) 5 ÷ (a +b) 2的结果吗
1.填空
① a 5 · ( )= a 9
② ( )· ( -b )2 = ( -b )7
③ x 6 ÷( )=x
④ ( ) ÷ ( -y )3 = ( -y )7
练习 课本第24页
2.计算
① a 10 ÷a 2
② ( ) · (-b) 2 = (-b)7
③ x 6 ÷ ( )=x
④ ( ) ÷ (-y)3 = (-y)7
1.计算
① 9 3 × 9 5 =
② 3 5 ×27 =
③ a 7 · a 8 =
④ x 2 · x 3 · x 4 =
习题12.4 课本第24页
2.计算
① (10 3 )5 =
② (a 3 )7 =
③ (x 2 )4 =
④ (a 2 )3 · a 5 =
3.判断下列等式是否正确,并说明理由
①(a 2 )3 = a 5
② a 2 · b 2 =(ab)4
③ a 12 = (a 2 )6 = (a 3 )4= (a 5 )7
4.计算
①(3 ×10 5) 2 ②(2x) 2
③(-2x) 3 ④a 2 · (ab) 3
⑤(ab) 3 ·(ac) 4
5.计算:
① (2x) 2
② (-a) 6÷(-a) 4
③(p3) 2÷p5
④ a10÷(-a2) 3
6.判断下列计算是否正确,如果不正确,请予以改正:
(1)(a 2 b) 2 =a 2 b 2
(2)a 6 ÷a 2 =a 3
(3)(3xy 2) 2÷6x 2 y 4
(4)(-m) 7 ÷(-m) 2 =m 5.
7.计算:
(1)(a 3) 6 ÷(a 4) 2
(2)(x 6 y) 6 ÷(x 2 y) 3
(3)x 2 · ( y 2 ) 6 ÷ x 5
(4) ( y 3 ) 3 ÷ y 3 ÷(- y 2) 2
8.用多少张边长为a的正方形硬纸卡片,能出个新的正方形 试写出三个答案,并用两种方法表示新正方形的面积从不同的表示方法中,你能发现什么
12.1 幂的运算
1. 同底数幂的乘法
试一试
根据幂的意义填空:
23 × 24 = (2 × 2 × 2) × (2 × 2 × 2 × 2)= 2( )
(2)53 × 54 = ___________________________ = 5( )
(3)a3 × a4=___________________________ = a( )
概括
am × an = (a · a · a) (a · a· …… · a)= 2( )
= a · a · a · a · a· …… · a = am+n
(m+n)个
可得am · an == am+n (mn为正整数)
这就是说,同底数幂相乘,底数不变,指数相加.
例1计算:
103×104 =
(2)a · a3 =
(3)a·a3 · a5=
1.判断下列计算是否正确,并说明理由:
(l)a·a2=a2 (3)a+a2=a3
(2)a3+a3 =a9 (4)a3+a3=a6
2.计算:
(1) 105×105 (2) a3×a7 (3) x·x5·x7
2.幂的乘方
试一试
根据乘方的意义及同底数幂的乘法法则填空
①(23)2 = 23 × 23 = 2( )
②(52)3 = 52 × 52 × 52 = 5( )
③(a3)4 = a3 × a3 × a3 × a3 = a( )
概括
( am )n = (am · am · am · am· …… · a)
= am+m+m+m+m+m+m+m+m+m
= amn
( am )n= amn
(m,n为正整数)
这就是说,幂的乘方,底数不变,指数相乘
例题2
计算
① ( 103 )5 = 103 ×5 = 1015
② ( b5 )4= b5×4 = b20
1.判断下列计算是否正确,并说明理由:
① ( a3 )5 = a8
② a3 · a5= a15
③( a2 )3 · a4 = a9
练习
2.计算
①( 22 )2 = ② ( y2 )5 =
③ ( x4 )3 = ④ ( y3 )2 ·( y2) 3 =
练习
3.积的乘方
试一试
根据乘方的意义和乘法运算律填空:
(1)(ab) 2 =(ab)·(ab) (2)(ab) 3
=(aa)·(bb) =__________________
=a( )b( ) =a( )b( )
(3)(ab) 4
=__________________
=a( )b( )
概括
(ab) n
= (ab) · (ab) ·…… · (ab)
= (a · a · a · a) · (b · b · b · b · b)
=a n b n
可得 (ab) n =a n b n (n为正整数)
这就是说,积的乘方,把积的每一个因式分别乘方再把所得的幕相乘。
例题3
例3计算:
(1)(2b) 3 =
(2)(2a 3 ) 2 =
(3)(-a) 3 =
(4)(-3x) 4 =
1.判断下列计算是否正确,并说明理由:
(1)(xy 3) 2 =xy 6
(2)(-2x ) 3 =-6x3
练习 课本第21页
2.计算:
(1)(3a) 2 =
(2)(-3a) 3 =
(3) (ab 2 ) 2 =
(4)(-2×10 3 ) 3 =
练习 课本第21页
4.同底数幂的除法
我们已经知道同底数幂的乘法法则:a m ·a n =a m +n ,那么同底数幂怎么相除呢
用你熟悉的方法计算:
①2 5 ÷2 2 =_____ ②10 7 ÷103 = _____
③ a 7 ÷ a 3 =_________ (a≠0).
由上面的计算,我们发现:
①2 5 ÷2 2 =
②10 7 ÷103 =
③ a 7 ÷ a 3 = (a≠0).
概括
般地设m、n为正整数,m>n,a≠0,有
这就是说,同底数幂相除,底数不变,指数相减
读一读
根据除法的意义推导同底数幂的除法法则前面我们通过一些计算,归纳、探索出同底数幂的除法法则.下面我们根据除法的意义来推导同底数幂的除法法则:
因为除法是乘法的逆运算,计算a m ÷a n (m、n都是正整数,且m>n,a≠0)实际上是要求一个式子,使
a m · ( )=a n
假设这个式子是a(是正整数,待定),即应有
a n · a k = a m
即a n +k = a m
所以n+k=m
得k=m-n
因此,要求的式子应该是a m-n
由同底数幂的乘法法则,可知
a n · a m-n = a n+(m-n) = a m
所以a m-n满足要求,从而有
a m÷a n=a m-n (m、n都是正整数,且m>n,a≠0)
例题4
计算
思考 你能用(a+b)的幂表示 (a+b) 5 ÷ (a +b) 2的结果吗
1.填空
① a 5 · ( )= a 9
② ( )· ( -b )2 = ( -b )7
③ x 6 ÷( )=x
④ ( ) ÷ ( -y )3 = ( -y )7
练习 课本第24页
2.计算
① a 10 ÷a 2
② ( ) · (-b) 2 = (-b)7
③ x 6 ÷ ( )=x
④ ( ) ÷ (-y)3 = (-y)7
1.计算
① 9 3 × 9 5 =
② 3 5 ×27 =
③ a 7 · a 8 =
④ x 2 · x 3 · x 4 =
习题12.4 课本第24页
2.计算
① (10 3 )5 =
② (a 3 )7 =
③ (x 2 )4 =
④ (a 2 )3 · a 5 =
3.判断下列等式是否正确,并说明理由
①(a 2 )3 = a 5
② a 2 · b 2 =(ab)4
③ a 12 = (a 2 )6 = (a 3 )4= (a 5 )7
4.计算
①(3 ×10 5) 2 ②(2x) 2
③(-2x) 3 ④a 2 · (ab) 3
⑤(ab) 3 ·(ac) 4
5.计算:
① (2x) 2
② (-a) 6÷(-a) 4
③(p3) 2÷p5
④ a10÷(-a2) 3
6.判断下列计算是否正确,如果不正确,请予以改正:
(1)(a 2 b) 2 =a 2 b 2
(2)a 6 ÷a 2 =a 3
(3)(3xy 2) 2÷6x 2 y 4
(4)(-m) 7 ÷(-m) 2 =m 5.
7.计算:
(1)(a 3) 6 ÷(a 4) 2
(2)(x 6 y) 6 ÷(x 2 y) 3
(3)x 2 · ( y 2 ) 6 ÷ x 5
(4) ( y 3 ) 3 ÷ y 3 ÷(- y 2) 2
8.用多少张边长为a的正方形硬纸卡片,能出个新的正方形 试写出三个答案,并用两种方法表示新正方形的面积从不同的表示方法中,你能发现什么
