2023-2024学年华师大版数学八年级上册课件12.2 整式的乘法课件 58张PPT
文档属性
| 名称 | 2023-2024学年华师大版数学八年级上册课件12.2 整式的乘法课件 58张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 1016.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-01 07:16:51 | ||
图片预览




文档简介
(共58张PPT)
12.2 整式的乘法
1.单项式与单项式机乘
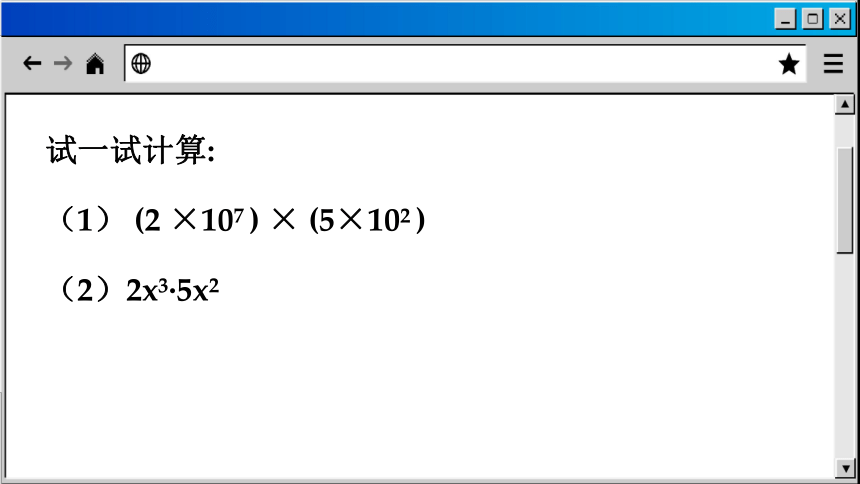
试一试计算:
(1) (2 ×107 ) × (5×102 )
(2)2x3·5x2
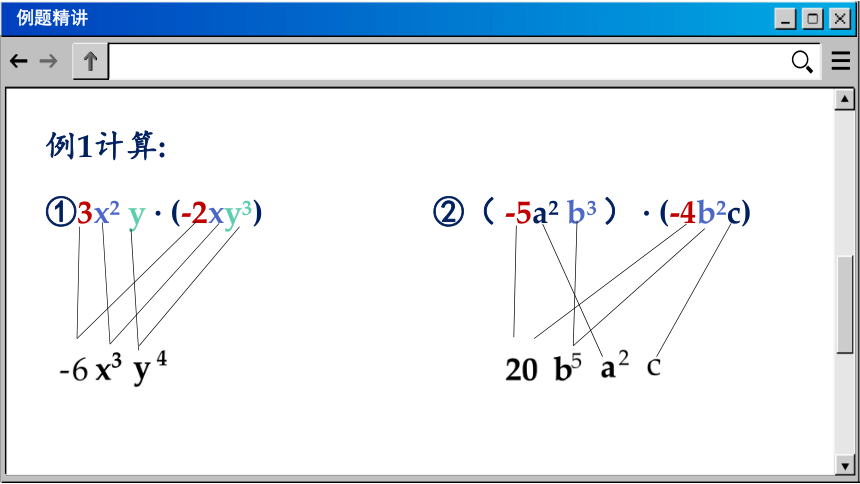
例1计算:
①3x2 y · (-2xy3) ②( -5a2 b3 ) · (-4b2c)
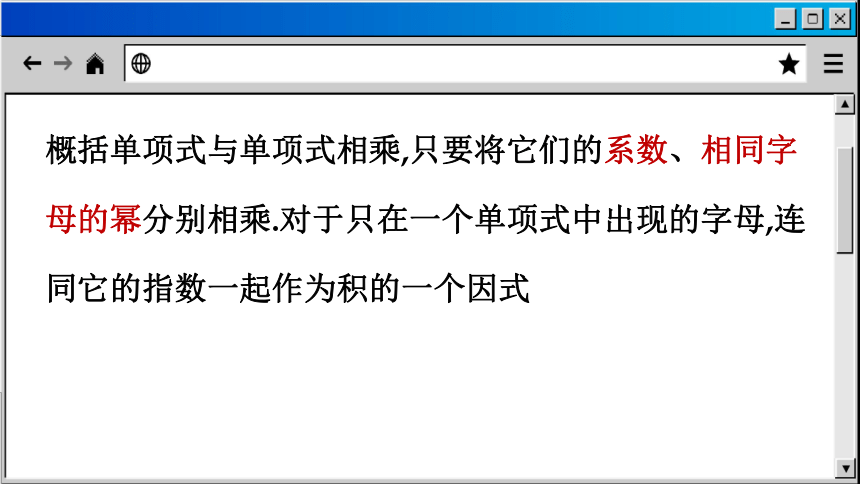
概括单项式与单项式相乘,只要将它们的系数、相同字母的幂分别相乘.对于只在一个单项式中出现的字母,连同它的指数一起作为积的一个因式
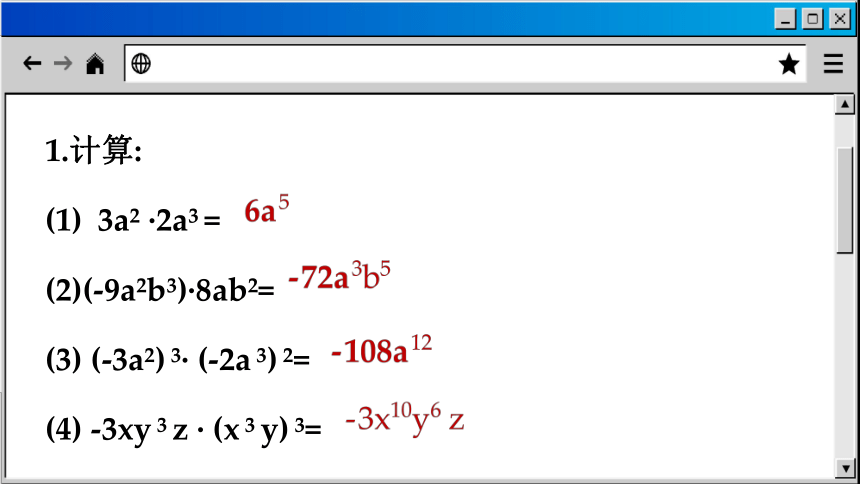
1.计算:
3a2 ·2a3 =
(2)(-9a2b3)·8ab2=
(3) (-3a2) 3· (-2a 3) 2=
(4) -3xy 3 z · (x 3 y) 3=
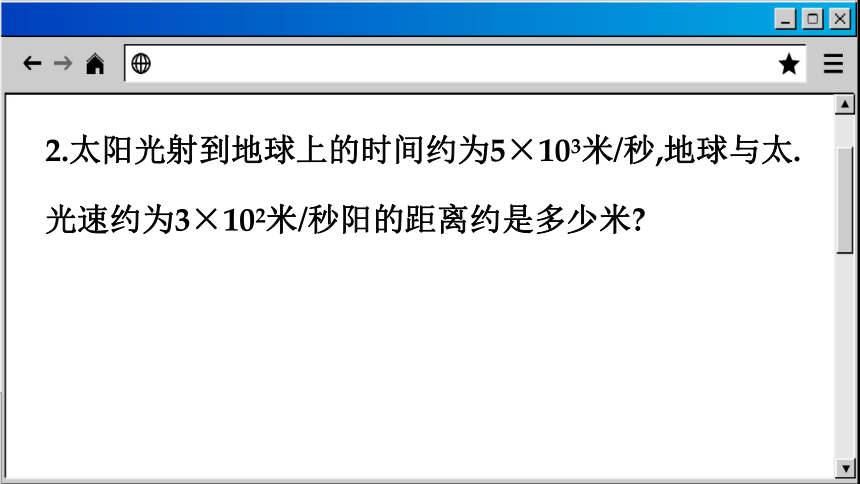
2.太阳光射到地球上的时间约为5×103米/秒,地球与太.光速约为3×102米/秒阳的距离约是多少米
3.小明的步长为a厘米,他量得一间屋子长15 步、宽 14 步,这间屋子的面积是多少平方厘米
2.单项式与多项式相乘
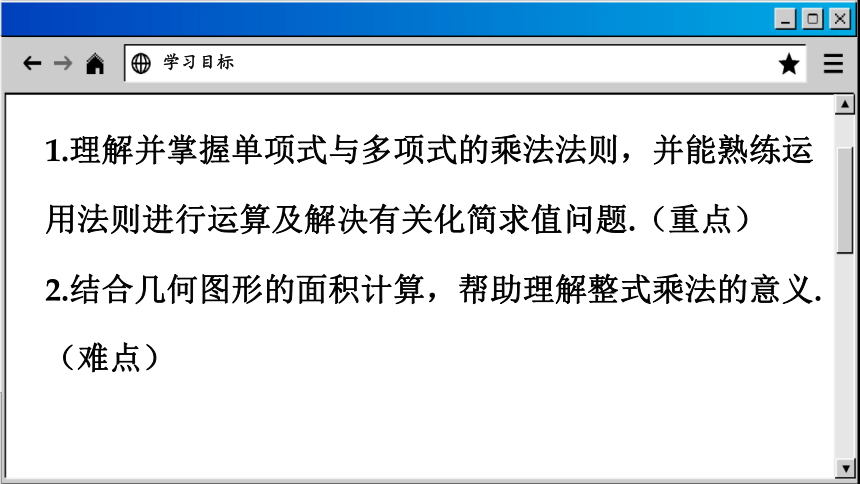
1.理解并掌握单项式与多项式的乘法法则,并能熟练运用法则进行运算及解决有关化简求值问题.(重点)
2.结合几何图形的面积计算,帮助理解整式乘法的意义.(难点)
学习目标
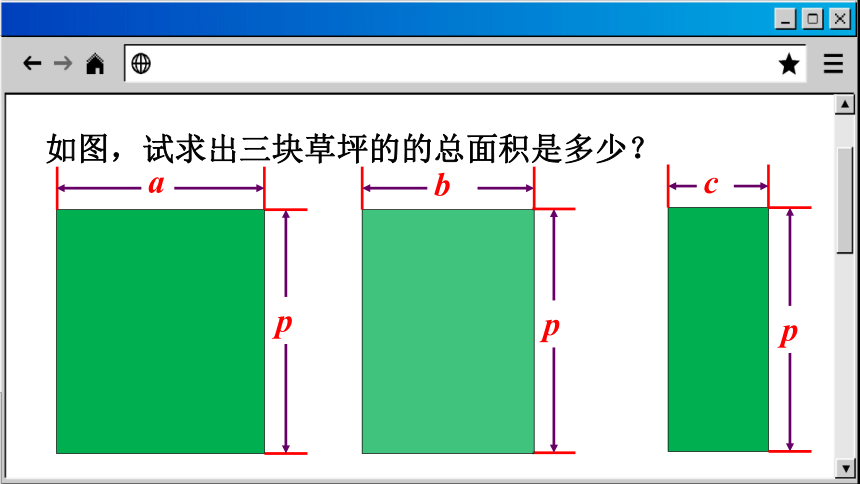
如图,试求出三块草坪的的总面积是多少?
p
p
a
b
p
c
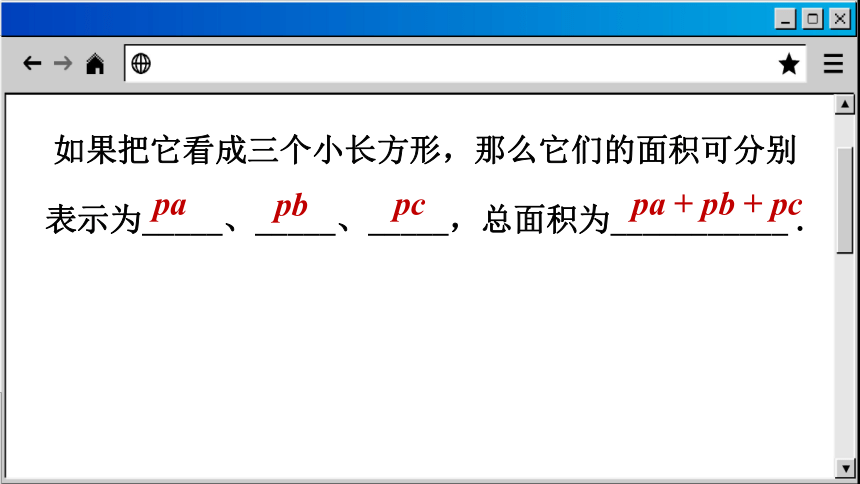
如果把它看成三个小长方形,那么它们的面积可分别
表示为_____、_____、_____,总面积为___________ .
pa
pc
pb
pa + pb + pc
p
a
p
p
c
b
如果把三个小长方形拼成一个大长方形,那么它们的总面积可以表示为________________.
p(a + b + c)
pa + pb + pc
p (a + b + c)
p ( a + b + c )
pb
+
pc
pa
+
根据乘法的分配律
试一试
计算:2a2 · (3a2-5b).
解:原式 = 2a2·3a2 + 2a2· (-5b)
= 6a4 -10a2b.
方法总结:根据乘法分配律,将单项式乘多项式的每一项,然后求和.
单项式与多项式相乘
单项式与多项式的乘法法则
单项式与多项式相乘,用单项式分别乘以多项式的每一项,再将所得的积相加.
p
b
p
a
p
c
p (a + b + c) = pa + pb + pc
注意
(1)依据是乘法分配律;
(2)积的项数与多项式的项数相同.
例题1
计算:
(1) 2ab (5ab2 + 3a2b); (2) (ab2-2ab) · ab
= 2ab · 5ab2 + 2ab · 3a2b
= 10a2b3 + 6a3b2.
(3) 5m2n (2n + 3m- n2);
(4) 2( x + y2z + xy2z3 ) · xyz.
= 5m2n · 2n + 5m2n · 3m + 5m2n · (-n2)
=10m2n2 + 15m3n- 5m2n3.
= (2x + 2y2z + 2xy2z3) · xyz
= 2x2yz+2xy3z2+2x2y3z4.
例2 一条防洪堤坝,其横断面是梯形,上底宽 a m,
下底宽 (a+2b) m,坝高a m.
(1) 求防洪堤坝的横断面面积;
解:(1) [ a+(a+2b) ]× a
= a (2a+2b)
= a2+ ab (m2).
故防洪堤坝的横断面面积为 a2+ ab m2.
(2) 如果防洪堤坝长 100 m,那么这段防洪堤坝的体
积是多少 m3?
( a2+ ab)×100=50a2+50ab (m3).
故这段防洪堤坝的体积为 50a2+50ab m3.
例3 先化简,再求值:
5a(2a2-5a+3)-2a2(5a+5)+7a2,其中 a=2.
解:5a(2a2-5a+3)-2a2(5a+5)+7a2
=10a3-25a2+15a-10a3-10a2+7a2
=-28a2+15a
当 a=2 时,原式=-82.
方法总结:
在计算时要注意先化简然后再代值计算.
整式的加减运算实际上就是去括号与合并同类项.
1.单项式与多项式相乘,就是用单项式分别乘以多项式的________,再将所得的积________.
2. 4(a - b + 1) =____________.
3. 3x(2x - y2) =____________.
4. (2x - 5y + 6z)(-3x) =__________________.
5. (-2a2)2 (-a - 2b + c) =_________________.
每一项
相加
4a - 4b + 4
6x2 - 3xy2
-6x2 + 15xy - 18xz
-4a5 - 8a4b + 4a4c
6. 计算:- 2x2 · ( xy + y2 ) - 5x(x2y - xy2).
解: = ( -2x2)·xy + (-2x2)·y2 + (-5x)·x2y + (-5x)·(-xy2)
= -2x3y + (-2x2y2) + (-5x3y) + 5x2y2
= -7x3y + 3x2y2.
注意
(1) 2x2 与 5x 前面的“ - ”不能看漏;
(2) 单项式与多项式相乘的结果中,应将 同类项 合并.
7.先化简,再求值 3a(2a2 - 4a + 3) - 2a2(3a + 4),
其中 a = -2.
解:3a(2a2 - 4a + 3) - 2a2(3a + 4)
= 6a3 - 12a2 + 9a - 6a3 - 8a2
= -20a2 + 9a.
当 a = -2 时,原式 = -20×(-2)2 + 9×(-2) = -98.
8. 如图,一块长方形地用来建造住宅、广场、商厦,求这块地的总面积.
解:4a [(3a + 2b) + (2a-b)]
= 4a (5a + b)
= 4a · 5a + 4a · b
= 20a2 + 4ab. 答:这块地的总面积为20a2 + 4ab.
住宅用地
人民广场
商业用地
3a
3a + 2b
2a-b
4a
3.多项式与多项式相乘
1.理解并掌握多项式与多项式的乘法运算法则.(重点)
2.能够用多项式与多项式的乘法运算法则进行计算.(难点)
学习目标
1. 如何进行单项式与多项式乘法的运算?
① 将单项式分别乘以多项式的各项;
② 再将所得的积相加.
复习引入
2. 进行单项式与多项式乘法运算时,要注意什么
① 不能漏乘:
即单项式要乘遍多项式的每一项;
② 去括号时注意符号的确定.
提出问题
问题1 (a + b) X =
当 X = m + n 时,(a + b) X =
(a + b) X = aX + bX
(a + b) X = (a + b) (m + n)
多项式乘多项式
问题2 某地区在退耕还林期间,有一块原长 m 米,宽为 a 米的长方形林区增长了 n 米,加宽了 b 米,请你表示这块林区现在的面积.
a
m
b
n
你能用不同的形式表示所拼图的面积吗?
ma
na
mb
nb
a
m
b
n
这块林区现在长为
(m + n) 米,
宽为 (a + b) 米.
由于 (m + n)(a + b) 和 (ma + mb + na + nb) 表示同一块地的面积,故有:
(m + n)(a + b) =
ma
+ mb
+ na
+ nb.
如何进行多项式与多项式相乘的运算?
实际上,把 (m + n) 看成一个整体,有:
= ma + mb + na + nb.
(m + n)(a + b)
= (m + n)a + (m + n)b
多项式乘多项式
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
1
2
3
4
(a + b)(m + n)
=
am
1
2
3
4
+ an
+ bm
+ bn
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
例 计算:
(1)( 3x + 1 )( x + 2 )
(2)( x - 8 )( x - y )
= x · x - xy - 8x + 8y = x2 - xy - 8x + 8y.
= 3x · x + 2×3x + 1 · x + 1×2
= 3x2 + 6x + x + 2 = 3x2 + 7x + 2.
(3) ( x + y )( x2 - xy + y2 ).
= x·x2 - x · xy + xy2 + x2y - xy2 + y · y2
= x3 - x2y + xy2 + x2y - xy2 + y3 = x3 + y3.
注意
需要注意的几个问题:
(1)漏乘;(2)符号问题;(3)最后结果应化成最简形式.
1.判断下列解法是否正确,若不正确请说出理由.
解:原式
当堂练习
解:原式
2.计算:(1) (x 3y)(x + 7y); (2) (2x + 5y)(3x 2y).
= x2 + 4xy 21y2.
解:(1) 原式 = x2 + 7xy 3yx 21y2
(2) 原式 = 2x 3x 2x 2y + 5 y 3x 5y 2y
= 6x2 4xy + 15xy 10y2
= 6x2 + 11xy 10y2.
3. 化简求值:(4x + 3y)(4x-3y) + (2x + y)(3x-5y),其中 x = 1,y =-2.
解:原式 =
当 x = 1,y = -2 时,原式 = 22×12-7×1×(-2)
-14×(-2)2 = 22 + 14-56 = -20.
4. 计算:
5 6
(-3) (-4)
2 (-8)
(-5) 6
观察上面四个等式,你能发现什么规律?并应用这个规律解决下面的问题.
口答:
七年级(下)
姓名:__________
数学
c
b
a
5. 小东找来一张挂历画包数学课本.已知课本长 a 厘米,宽 b 厘米,厚 c 厘米,小东想将课本封面与封底的每一边都包进去 m 厘米,问小东应在挂历画上裁下一块多大面积的长方形?
a
b
c
m
b
m
面积:
(2m + 2b + c)(2m + a)
解:(2m + 2b + c)(2m + a)
= 4m2 + 2ma + 4bm + 2ab + 2cm + ca.
答:小东应在挂历画上裁下一块 (4m2 + 2ma + 4bm
+ 2ab + 2cm + ca) 平方厘米的长方形.
整式的乘法
单项式乘以多项式
注意
课堂小结
多项式乘多项式
运算法则
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加
(a + b)(m + n) = am + an + bm + bn
注意
不要漏乘,正确确定各项符号;结果要最简
实质上是转化为单项式×多项式的运算
(x-1)2=(x-1)(x-1),而不是x2-12
课堂小结
12.2 整式的乘法
1.单项式与单项式机乘
试一试计算:
(1) (2 ×107 ) × (5×102 )
(2)2x3·5x2
例1计算:
①3x2 y · (-2xy3) ②( -5a2 b3 ) · (-4b2c)
概括单项式与单项式相乘,只要将它们的系数、相同字母的幂分别相乘.对于只在一个单项式中出现的字母,连同它的指数一起作为积的一个因式
1.计算:
3a2 ·2a3 =
(2)(-9a2b3)·8ab2=
(3) (-3a2) 3· (-2a 3) 2=
(4) -3xy 3 z · (x 3 y) 3=
2.太阳光射到地球上的时间约为5×103米/秒,地球与太.光速约为3×102米/秒阳的距离约是多少米
3.小明的步长为a厘米,他量得一间屋子长15 步、宽 14 步,这间屋子的面积是多少平方厘米
2.单项式与多项式相乘
1.理解并掌握单项式与多项式的乘法法则,并能熟练运用法则进行运算及解决有关化简求值问题.(重点)
2.结合几何图形的面积计算,帮助理解整式乘法的意义.(难点)
学习目标
如图,试求出三块草坪的的总面积是多少?
p
p
a
b
p
c
如果把它看成三个小长方形,那么它们的面积可分别
表示为_____、_____、_____,总面积为___________ .
pa
pc
pb
pa + pb + pc
p
a
p
p
c
b
如果把三个小长方形拼成一个大长方形,那么它们的总面积可以表示为________________.
p(a + b + c)
pa + pb + pc
p (a + b + c)
p ( a + b + c )
pb
+
pc
pa
+
根据乘法的分配律
试一试
计算:2a2 · (3a2-5b).
解:原式 = 2a2·3a2 + 2a2· (-5b)
= 6a4 -10a2b.
方法总结:根据乘法分配律,将单项式乘多项式的每一项,然后求和.
单项式与多项式相乘
单项式与多项式的乘法法则
单项式与多项式相乘,用单项式分别乘以多项式的每一项,再将所得的积相加.
p
b
p
a
p
c
p (a + b + c) = pa + pb + pc
注意
(1)依据是乘法分配律;
(2)积的项数与多项式的项数相同.
例题1
计算:
(1) 2ab (5ab2 + 3a2b); (2) (ab2-2ab) · ab
= 2ab · 5ab2 + 2ab · 3a2b
= 10a2b3 + 6a3b2.
(3) 5m2n (2n + 3m- n2);
(4) 2( x + y2z + xy2z3 ) · xyz.
= 5m2n · 2n + 5m2n · 3m + 5m2n · (-n2)
=10m2n2 + 15m3n- 5m2n3.
= (2x + 2y2z + 2xy2z3) · xyz
= 2x2yz+2xy3z2+2x2y3z4.
例2 一条防洪堤坝,其横断面是梯形,上底宽 a m,
下底宽 (a+2b) m,坝高a m.
(1) 求防洪堤坝的横断面面积;
解:(1) [ a+(a+2b) ]× a
= a (2a+2b)
= a2+ ab (m2).
故防洪堤坝的横断面面积为 a2+ ab m2.
(2) 如果防洪堤坝长 100 m,那么这段防洪堤坝的体
积是多少 m3?
( a2+ ab)×100=50a2+50ab (m3).
故这段防洪堤坝的体积为 50a2+50ab m3.
例3 先化简,再求值:
5a(2a2-5a+3)-2a2(5a+5)+7a2,其中 a=2.
解:5a(2a2-5a+3)-2a2(5a+5)+7a2
=10a3-25a2+15a-10a3-10a2+7a2
=-28a2+15a
当 a=2 时,原式=-82.
方法总结:
在计算时要注意先化简然后再代值计算.
整式的加减运算实际上就是去括号与合并同类项.
1.单项式与多项式相乘,就是用单项式分别乘以多项式的________,再将所得的积________.
2. 4(a - b + 1) =____________.
3. 3x(2x - y2) =____________.
4. (2x - 5y + 6z)(-3x) =__________________.
5. (-2a2)2 (-a - 2b + c) =_________________.
每一项
相加
4a - 4b + 4
6x2 - 3xy2
-6x2 + 15xy - 18xz
-4a5 - 8a4b + 4a4c
6. 计算:- 2x2 · ( xy + y2 ) - 5x(x2y - xy2).
解: = ( -2x2)·xy + (-2x2)·y2 + (-5x)·x2y + (-5x)·(-xy2)
= -2x3y + (-2x2y2) + (-5x3y) + 5x2y2
= -7x3y + 3x2y2.
注意
(1) 2x2 与 5x 前面的“ - ”不能看漏;
(2) 单项式与多项式相乘的结果中,应将 同类项 合并.
7.先化简,再求值 3a(2a2 - 4a + 3) - 2a2(3a + 4),
其中 a = -2.
解:3a(2a2 - 4a + 3) - 2a2(3a + 4)
= 6a3 - 12a2 + 9a - 6a3 - 8a2
= -20a2 + 9a.
当 a = -2 时,原式 = -20×(-2)2 + 9×(-2) = -98.
8. 如图,一块长方形地用来建造住宅、广场、商厦,求这块地的总面积.
解:4a [(3a + 2b) + (2a-b)]
= 4a (5a + b)
= 4a · 5a + 4a · b
= 20a2 + 4ab. 答:这块地的总面积为20a2 + 4ab.
住宅用地
人民广场
商业用地
3a
3a + 2b
2a-b
4a
3.多项式与多项式相乘
1.理解并掌握多项式与多项式的乘法运算法则.(重点)
2.能够用多项式与多项式的乘法运算法则进行计算.(难点)
学习目标
1. 如何进行单项式与多项式乘法的运算?
① 将单项式分别乘以多项式的各项;
② 再将所得的积相加.
复习引入
2. 进行单项式与多项式乘法运算时,要注意什么
① 不能漏乘:
即单项式要乘遍多项式的每一项;
② 去括号时注意符号的确定.
提出问题
问题1 (a + b) X =
当 X = m + n 时,(a + b) X =
(a + b) X = aX + bX
(a + b) X = (a + b) (m + n)
多项式乘多项式
问题2 某地区在退耕还林期间,有一块原长 m 米,宽为 a 米的长方形林区增长了 n 米,加宽了 b 米,请你表示这块林区现在的面积.
a
m
b
n
你能用不同的形式表示所拼图的面积吗?
ma
na
mb
nb
a
m
b
n
这块林区现在长为
(m + n) 米,
宽为 (a + b) 米.
由于 (m + n)(a + b) 和 (ma + mb + na + nb) 表示同一块地的面积,故有:
(m + n)(a + b) =
ma
+ mb
+ na
+ nb.
如何进行多项式与多项式相乘的运算?
实际上,把 (m + n) 看成一个整体,有:
= ma + mb + na + nb.
(m + n)(a + b)
= (m + n)a + (m + n)b
多项式乘多项式
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
1
2
3
4
(a + b)(m + n)
=
am
1
2
3
4
+ an
+ bm
+ bn
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
例 计算:
(1)( 3x + 1 )( x + 2 )
(2)( x - 8 )( x - y )
= x · x - xy - 8x + 8y = x2 - xy - 8x + 8y.
= 3x · x + 2×3x + 1 · x + 1×2
= 3x2 + 6x + x + 2 = 3x2 + 7x + 2.
(3) ( x + y )( x2 - xy + y2 ).
= x·x2 - x · xy + xy2 + x2y - xy2 + y · y2
= x3 - x2y + xy2 + x2y - xy2 + y3 = x3 + y3.
注意
需要注意的几个问题:
(1)漏乘;(2)符号问题;(3)最后结果应化成最简形式.
1.判断下列解法是否正确,若不正确请说出理由.
解:原式
当堂练习
解:原式
2.计算:(1) (x 3y)(x + 7y); (2) (2x + 5y)(3x 2y).
= x2 + 4xy 21y2.
解:(1) 原式 = x2 + 7xy 3yx 21y2
(2) 原式 = 2x 3x 2x 2y + 5 y 3x 5y 2y
= 6x2 4xy + 15xy 10y2
= 6x2 + 11xy 10y2.
3. 化简求值:(4x + 3y)(4x-3y) + (2x + y)(3x-5y),其中 x = 1,y =-2.
解:原式 =
当 x = 1,y = -2 时,原式 = 22×12-7×1×(-2)
-14×(-2)2 = 22 + 14-56 = -20.
4. 计算:
5 6
(-3) (-4)
2 (-8)
(-5) 6
观察上面四个等式,你能发现什么规律?并应用这个规律解决下面的问题.
口答:
七年级(下)
姓名:__________
数学
c
b
a
5. 小东找来一张挂历画包数学课本.已知课本长 a 厘米,宽 b 厘米,厚 c 厘米,小东想将课本封面与封底的每一边都包进去 m 厘米,问小东应在挂历画上裁下一块多大面积的长方形?
a
b
c
m
b
m
面积:
(2m + 2b + c)(2m + a)
解:(2m + 2b + c)(2m + a)
= 4m2 + 2ma + 4bm + 2ab + 2cm + ca.
答:小东应在挂历画上裁下一块 (4m2 + 2ma + 4bm
+ 2ab + 2cm + ca) 平方厘米的长方形.
整式的乘法
单项式乘以多项式
注意
课堂小结
多项式乘多项式
运算法则
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加
(a + b)(m + n) = am + an + bm + bn
注意
不要漏乘,正确确定各项符号;结果要最简
实质上是转化为单项式×多项式的运算
(x-1)2=(x-1)(x-1),而不是x2-12
课堂小结
