等边三角形[上学期]
图片预览




文档简介
课件20张PPT。14.3.2 等边三角形义务教育课程标准实验教科书
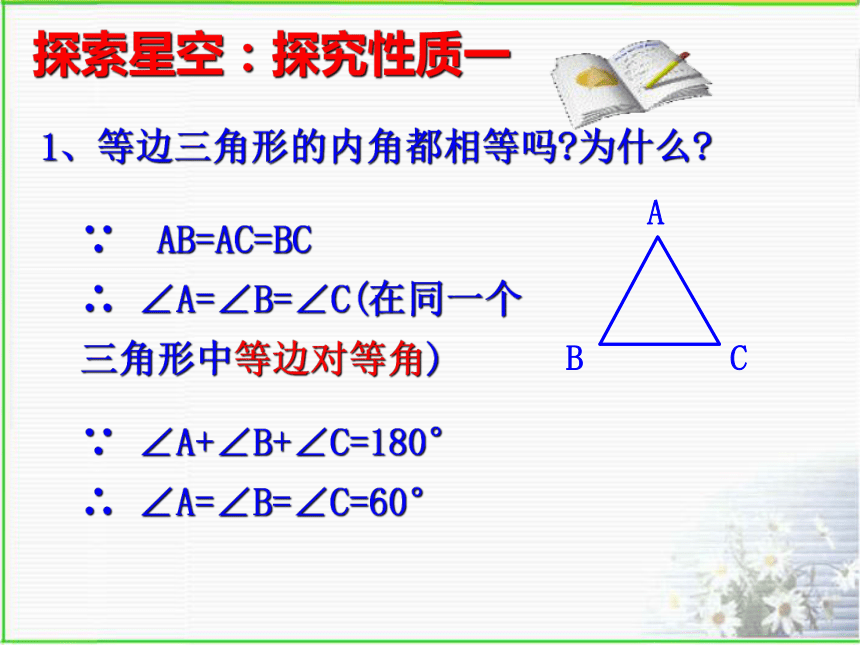
人教版《数学》八年级上册主讲:张佐香等边对等角三线合一等角对等边两边相等两腰相等轴对称图形知识回顾等边三角形:(正三角形)三条边都相等的三角形.等边三角形是特殊的等腰三角形.学习园地1、等边三角形的内角都相等吗?为什么?∵ AB=AC=BC
∴ ∠A=∠B=∠C(在同一个三角形中等边对等角)
∵ ∠A+∠B+∠C=180°
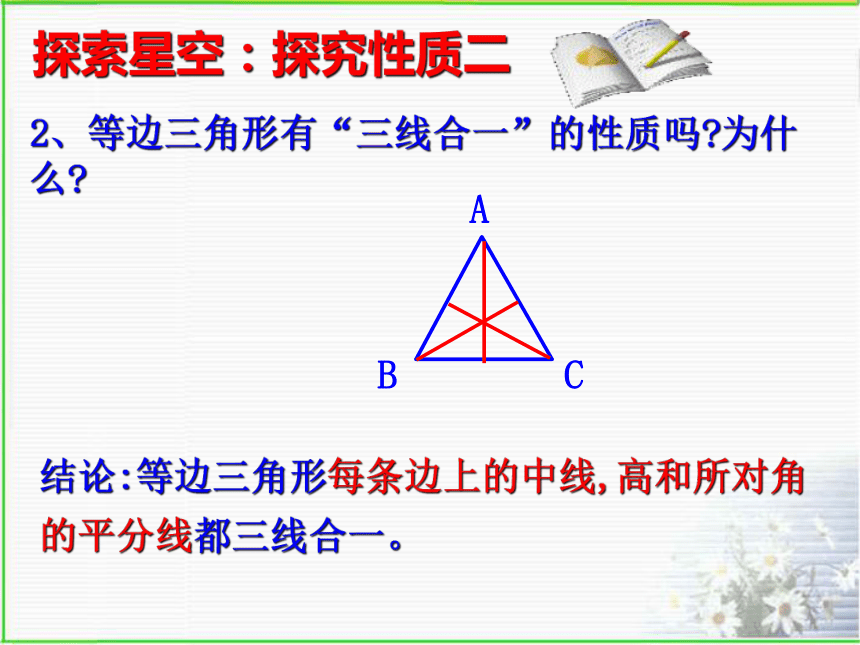
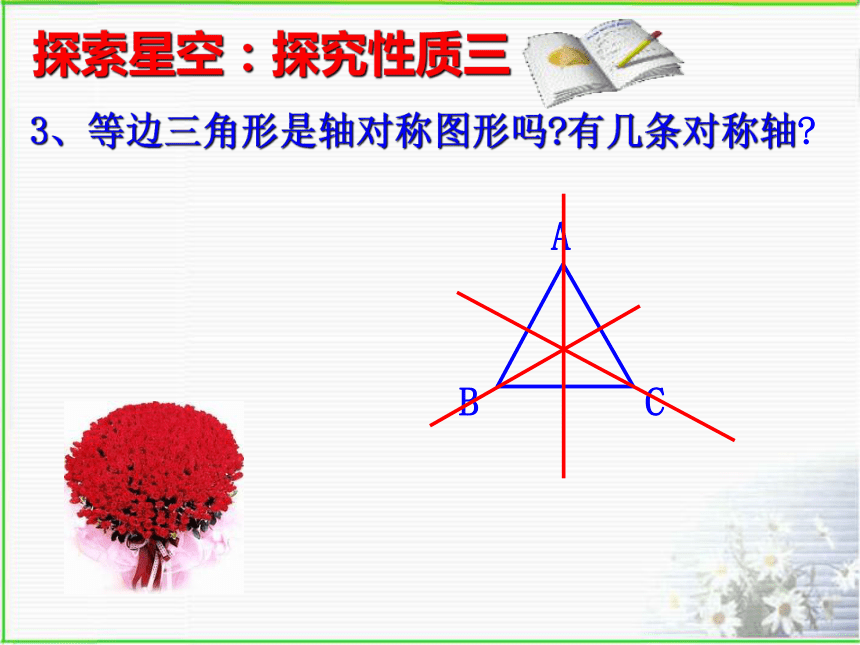
∴ ∠A=∠B=∠C=60°探索星空:探究性质一2、等边三角形有“三线合一”的性质吗?为什么?结论:等边三角形每条边上的中线,高和所对角的平分线都三线合一。探索星空:探究性质二3、等边三角形是轴对称图形吗?有几条对称轴?探索星空:探究性质三等边三角形的性质2.等边三角形的内角都相等,且等于60 °
3.等边三角形各边上中线,高和所对角的平分线都三线合一.4.等边三角形是轴对称图形,有三条对称轴.
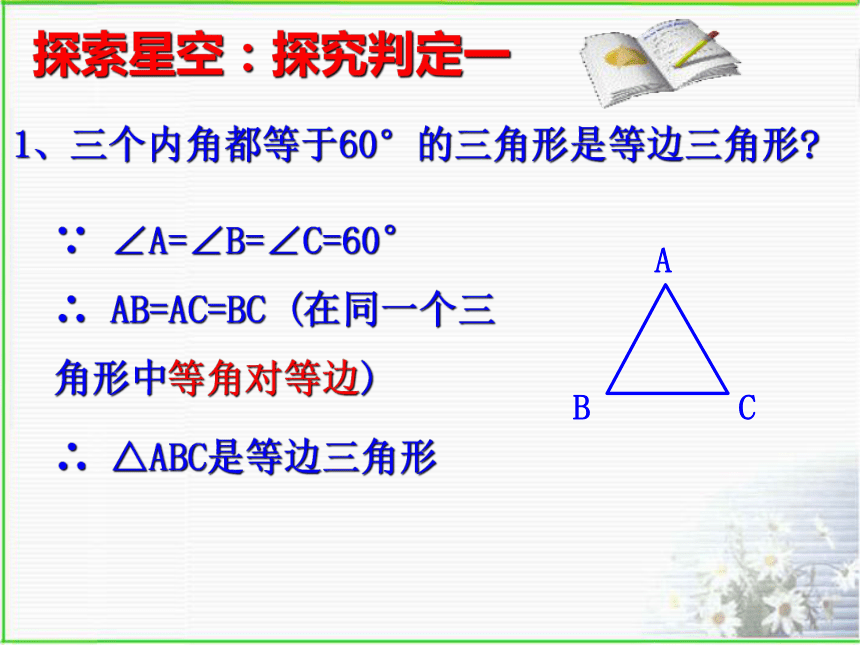
1 .三条边相等∵ ∠A=∠B=∠C=60°
∴ AB=AC=BC (在同一个三角形中等角对等边)探索星空:探究判定一1、三个内角都等于60°的三角形是等边三角形?∴ △ABC是等边三角形 2、有一个内角等于60°的等腰三角形是等边三角形?探索星空:探究判定二当顶角为60°时,两个底角各为60°.当底角为60°时,顶角为60°.等边三角形的判定方法:1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
尝试舞台例4 等边三角形ABC的周长等于21㎝,
求:(1)各边的长;
(2)各角的度数。
解:(1)∵AB=BC=CA,
又 ∵AB+BC+CA=21㎝(已知)
∴AB=BC=CA=21/3=7(㎝)
(2)∵AB=BC=CA,(已知)
∴∠A =∠B=∠C=60°
(等边三角形的每个内角都等于60°) ABC试一试你能行 1、下列四个说法中,不正确的有( )
(A)0个(B)1个(C)2个(D)3个
三个角都相等的三角形是等边三角形。
有两个角等于60°的三角形是等边三角形。
有一个是60°的等腰三角形是等边三角形。
有两个角相等的等腰三角形是等边三角形。
2、等边三角形的对称轴有( )
(A)1条(B)2条(C)3条(D)4条
3、等边三角形中,高、中线、角平分线共有( )
(A)3条(B)6条(C)9条(D)7条
?
(选择)BCA探究:如图,等边三角形ABC,以下三种方法分别得到的三角形ADE都是等边三角形吗?为什么?(1)在边AB,AC,分别截取AD=AE
(2)∠ADE=60°,D,E分别在边AB,AC上
(3)过边AB上D点,作DE∥BC,交
AC于E点体会.分享请你说一说这节课的收获和体验让大家与你一起分享 ?等边三角形的性质:三个角都相等,且都为60°三线合一三条边都相等轴对称图形,有三条对称轴等边三角形的判定:三个角都等于60°的三角形三条边都相等的三角形有一个角等于60°的等腰三角形教师寄语愿你用勤奋的汗水
浇灌智慧的花朵自主实践温顾所学作业:
教材p147—2题选做题:P150—11题反馈练习:等边三角形ABC的周长等于12㎝,
求:(1)各边的长;
(2)各角的度数。
人教版《数学》八年级上册主讲:张佐香等边对等角三线合一等角对等边两边相等两腰相等轴对称图形知识回顾等边三角形:(正三角形)三条边都相等的三角形.等边三角形是特殊的等腰三角形.学习园地1、等边三角形的内角都相等吗?为什么?∵ AB=AC=BC
∴ ∠A=∠B=∠C(在同一个三角形中等边对等角)
∵ ∠A+∠B+∠C=180°
∴ ∠A=∠B=∠C=60°探索星空:探究性质一2、等边三角形有“三线合一”的性质吗?为什么?结论:等边三角形每条边上的中线,高和所对角的平分线都三线合一。探索星空:探究性质二3、等边三角形是轴对称图形吗?有几条对称轴?探索星空:探究性质三等边三角形的性质2.等边三角形的内角都相等,且等于60 °
3.等边三角形各边上中线,高和所对角的平分线都三线合一.4.等边三角形是轴对称图形,有三条对称轴.
1 .三条边相等∵ ∠A=∠B=∠C=60°
∴ AB=AC=BC (在同一个三角形中等角对等边)探索星空:探究判定一1、三个内角都等于60°的三角形是等边三角形?∴ △ABC是等边三角形 2、有一个内角等于60°的等腰三角形是等边三角形?探索星空:探究判定二当顶角为60°时,两个底角各为60°.当底角为60°时,顶角为60°.等边三角形的判定方法:1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
尝试舞台例4 等边三角形ABC的周长等于21㎝,
求:(1)各边的长;
(2)各角的度数。
解:(1)∵AB=BC=CA,
又 ∵AB+BC+CA=21㎝(已知)
∴AB=BC=CA=21/3=7(㎝)
(2)∵AB=BC=CA,(已知)
∴∠A =∠B=∠C=60°
(等边三角形的每个内角都等于60°) ABC试一试你能行 1、下列四个说法中,不正确的有( )
(A)0个(B)1个(C)2个(D)3个
三个角都相等的三角形是等边三角形。
有两个角等于60°的三角形是等边三角形。
有一个是60°的等腰三角形是等边三角形。
有两个角相等的等腰三角形是等边三角形。
2、等边三角形的对称轴有( )
(A)1条(B)2条(C)3条(D)4条
3、等边三角形中,高、中线、角平分线共有( )
(A)3条(B)6条(C)9条(D)7条
?
(选择)BCA探究:如图,等边三角形ABC,以下三种方法分别得到的三角形ADE都是等边三角形吗?为什么?(1)在边AB,AC,分别截取AD=AE
(2)∠ADE=60°,D,E分别在边AB,AC上
(3)过边AB上D点,作DE∥BC,交
AC于E点体会.分享请你说一说这节课的收获和体验让大家与你一起分享 ?等边三角形的性质:三个角都相等,且都为60°三线合一三条边都相等轴对称图形,有三条对称轴等边三角形的判定:三个角都等于60°的三角形三条边都相等的三角形有一个角等于60°的等腰三角形教师寄语愿你用勤奋的汗水
浇灌智慧的花朵自主实践温顾所学作业:
教材p147—2题选做题:P150—11题反馈练习:等边三角形ABC的周长等于12㎝,
求:(1)各边的长;
(2)各角的度数。
