三角形的中位线[上学期]
图片预览




文档简介
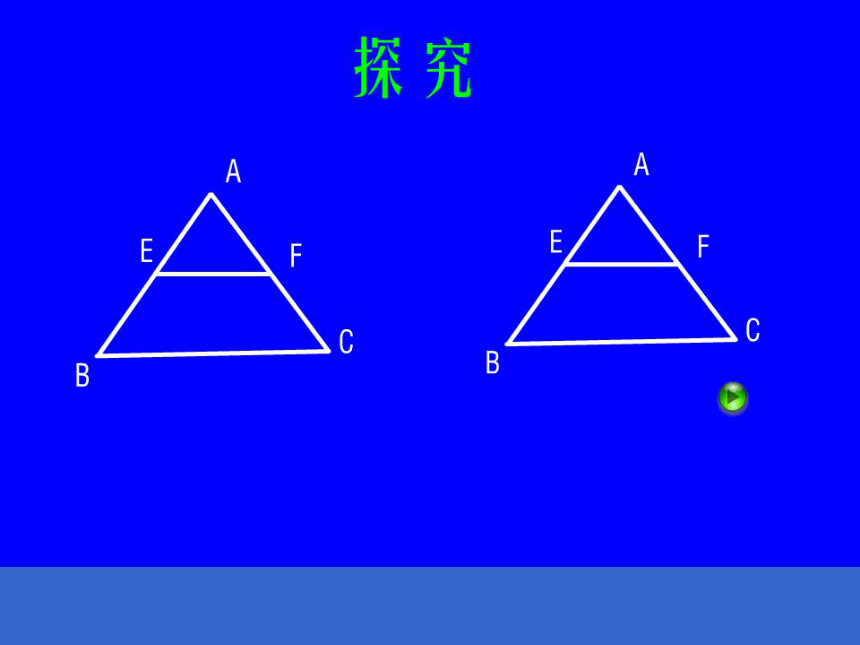
课件16张PPT。三角形的中位线义务教育课程标准实验教科书六都寨镇中学三角形的中位线定义:连结三角形两边中点的线段
叫做三角形的中位线D一个三角形有______条中位线三中位线的作法:先求得两边的中点,再作出这两点间的线段。E?三角形的中位线与三角形中线有什么区别? 中位线是连结三角形两边中点的线段中线是连结三角形一个顶点和它对边中点的线段 DE对比:三角形有三条中位线,它们组成一个三角形;
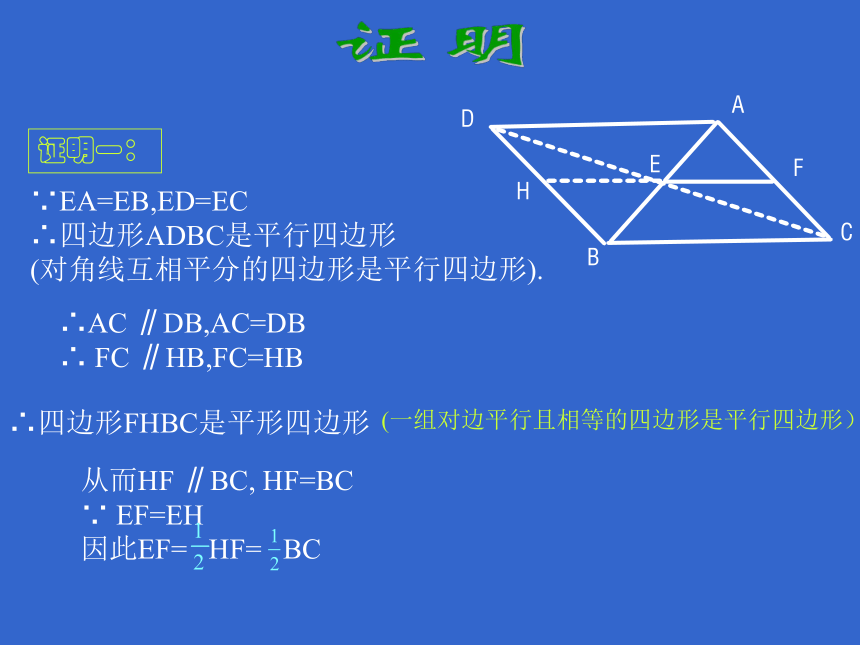
三角形有三条中线,它们相交于一点。证明证明一:∴AC ∥DB,AC=DB
∴ FC ∥HB,FC=HB(一组对边平行且相等的四边形是平行四边形)∵EA=EB,ED=EC
∴四边形ADBC是平行四边形
(对角线互相平分的四边形是平行四边形).∴四边形FHBC是平形四边形从而HF ∥BC, HF=BC
∵ EF=EH
因此EF= HF= BC
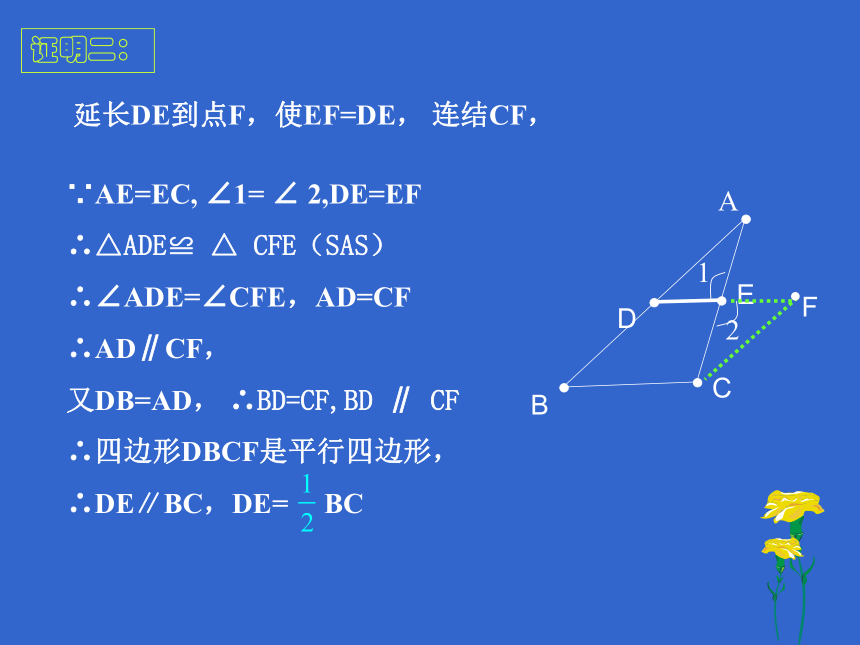
延长DE到点F,使EF=DE,2连结CF,∵AE=EC, ∠1= ∠ 2,DE=EF
∴△ADE≌ △ CFE(SAS)
∴∠ADE=∠CFE,AD=CF
∴AD∥CF,
又DB=AD, ∴BD=CF,BD ∥ CF
∴四边形DBCF是平行四边形,
∴DE∥BC,DE= BC 1 证明二:结论 三角形的中位线平行于第三边,
并且等于第三边的一半。例3、如图:顺次连结四边形ABCD各边中点E,F,H,M,得到的四边形EFHM是平行四边形吗?为什么?
例题讲解1、在例3中,设四边形ABCD的两条对角线AC,BD的长分别为5cm,4.4cm,点E,F,H,M分别是边AB,BC,CD,DA的中点,求平行四边形EFHM的周长?练习答案:∴平行四边形EFHM的周长=AC+DB=5+4.4=9.4(CM)∵ME=HF= DB;
MH=EF= AC;
2、已知△ABC的各边长度分别为3cm,3.4cm,4cm,则连结各边中点所成△DEF的周长等于 cm。练习答案:三角形各边中点所成的三角形的周长
是原三角形周长的一半5.2结论:3、如图,△ABC的边BC,CA,AB的中点分别是D,E,F。练习(1)四边形AFDE是平行四边形吗?为什么?
(2)四边形AFDE的周长等于AB+AC吗?为什么?练习答案:(1)四边形AFDE是平行四边形。
∵ DF= AC= AE, DE= AB=AF;
∴四边形AFDE是平行四边形。 3、如图,△ABC的边BC,CA,AB的中点分别是D,E,F。(1)四边形AFDE是平行四边形吗?为什么?
(2)四边形AFDE的周长等于AB+AC吗?为什么?(2)是。
∵DF+AE+DE+AF= AC+ AC+ AB+ AB=AC+AB。1、三角形中位线的概念。3、三角形中位线定理。2、三角形中位线与中线的区别。小结中位线是连结三角形两边中点的线段中位线是连结三角形两边中点的线段
中线是连结三角形一个顶点和它对边中点的线段三角形的中位线平行于第三边,并且等于第三边
的一半。作业1、习题3.1A组第13题
2、习题3.1 B组第 4 题谢 谢 指 导 !
叫做三角形的中位线D一个三角形有______条中位线三中位线的作法:先求得两边的中点,再作出这两点间的线段。E?三角形的中位线与三角形中线有什么区别? 中位线是连结三角形两边中点的线段中线是连结三角形一个顶点和它对边中点的线段 DE对比:三角形有三条中位线,它们组成一个三角形;
三角形有三条中线,它们相交于一点。证明证明一:∴AC ∥DB,AC=DB
∴ FC ∥HB,FC=HB(一组对边平行且相等的四边形是平行四边形)∵EA=EB,ED=EC
∴四边形ADBC是平行四边形
(对角线互相平分的四边形是平行四边形).∴四边形FHBC是平形四边形从而HF ∥BC, HF=BC
∵ EF=EH
因此EF= HF= BC
延长DE到点F,使EF=DE,2连结CF,∵AE=EC, ∠1= ∠ 2,DE=EF
∴△ADE≌ △ CFE(SAS)
∴∠ADE=∠CFE,AD=CF
∴AD∥CF,
又DB=AD, ∴BD=CF,BD ∥ CF
∴四边形DBCF是平行四边形,
∴DE∥BC,DE= BC 1 证明二:结论 三角形的中位线平行于第三边,
并且等于第三边的一半。例3、如图:顺次连结四边形ABCD各边中点E,F,H,M,得到的四边形EFHM是平行四边形吗?为什么?
例题讲解1、在例3中,设四边形ABCD的两条对角线AC,BD的长分别为5cm,4.4cm,点E,F,H,M分别是边AB,BC,CD,DA的中点,求平行四边形EFHM的周长?练习答案:∴平行四边形EFHM的周长=AC+DB=5+4.4=9.4(CM)∵ME=HF= DB;
MH=EF= AC;
2、已知△ABC的各边长度分别为3cm,3.4cm,4cm,则连结各边中点所成△DEF的周长等于 cm。练习答案:三角形各边中点所成的三角形的周长
是原三角形周长的一半5.2结论:3、如图,△ABC的边BC,CA,AB的中点分别是D,E,F。练习(1)四边形AFDE是平行四边形吗?为什么?
(2)四边形AFDE的周长等于AB+AC吗?为什么?练习答案:(1)四边形AFDE是平行四边形。
∵ DF= AC= AE, DE= AB=AF;
∴四边形AFDE是平行四边形。 3、如图,△ABC的边BC,CA,AB的中点分别是D,E,F。(1)四边形AFDE是平行四边形吗?为什么?
(2)四边形AFDE的周长等于AB+AC吗?为什么?(2)是。
∵DF+AE+DE+AF= AC+ AC+ AB+ AB=AC+AB。1、三角形中位线的概念。3、三角形中位线定理。2、三角形中位线与中线的区别。小结中位线是连结三角形两边中点的线段中位线是连结三角形两边中点的线段
中线是连结三角形一个顶点和它对边中点的线段三角形的中位线平行于第三边,并且等于第三边
的一半。作业1、习题3.1A组第13题
2、习题3.1 B组第 4 题谢 谢 指 导 !
