三角形的中位线[下学期]
图片预览



文档简介
课件15张PPT。平行四边形的判定
A 。。BC 。D。。
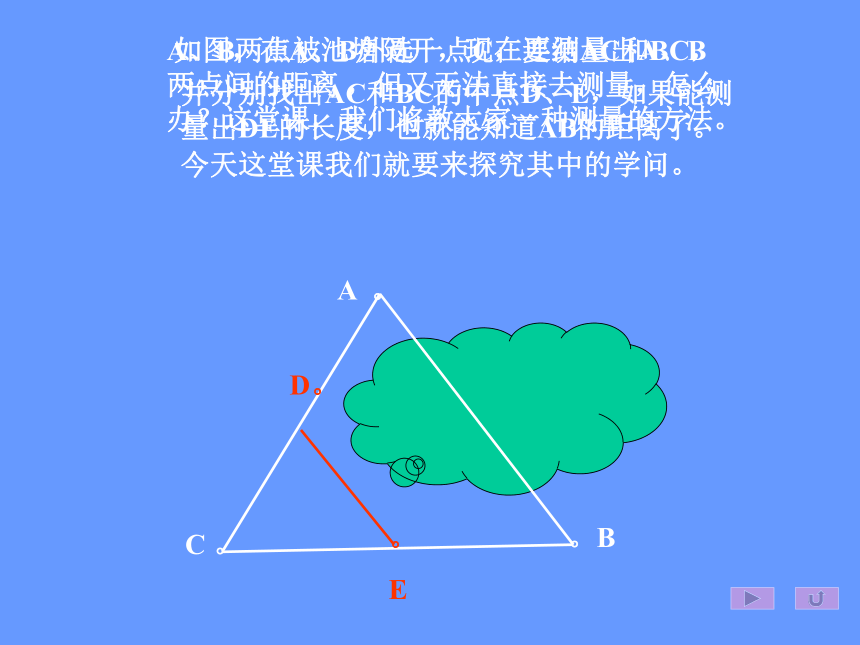
E如图,在A、B外选一点C,连结AC和BC,A、B两点被池塘隔开,现在要测量出A、B两点间的距离 ,但又无法直接去测量,怎么办?这堂课,我们将教大家一种测量的方法。并分别找出AC和BC的中点D、E,如果能测量出DE的长度,也就能知道AB的距离了。今天这堂课我们就要来探究其中的学问。
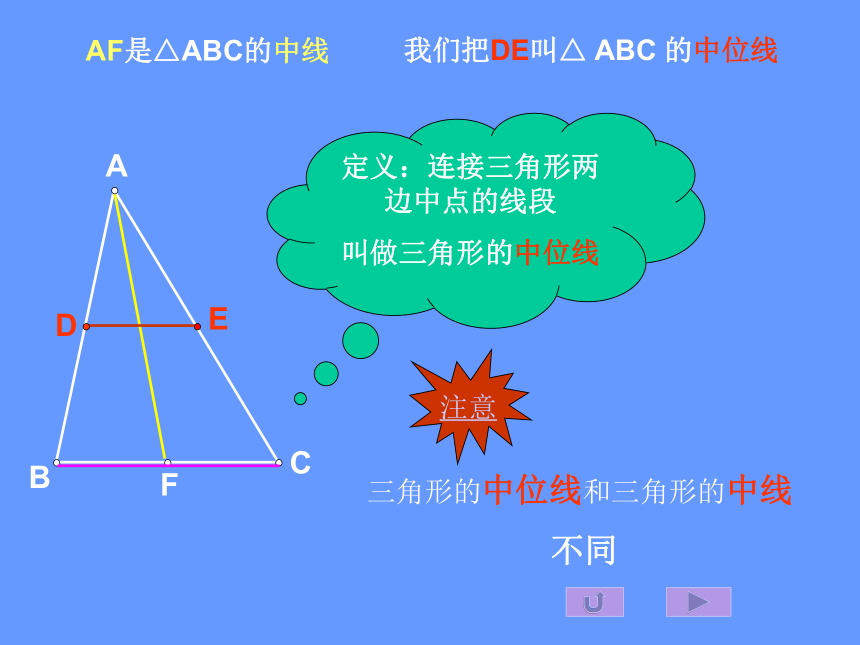
三角形的中位线和三角形的中线
不同CBAFED定义:连接三角形两边中点的线段
叫做三角形的中位线
AF是△ABC的中线我们把DE叫△ ABC 的中位线 注意:三角形的中位线是连结三角形两边中点的线段三角形的中线是连结一个顶点和它的对边中点的线段 区分三角形的中位线和中线: 理解三角形的中位线定义的两层含义:② ∵ DE为△ABC的中位线 ① ∵D、E分别为AB、AC的中点 ∴DE为△ABC的中位线∴ D、E分别为AB、AC的中点 一个三角形共有三条中位线。定义ABCD。。E。FABCDEF已知:在△ABC 中,DE是△ABC 的中位线
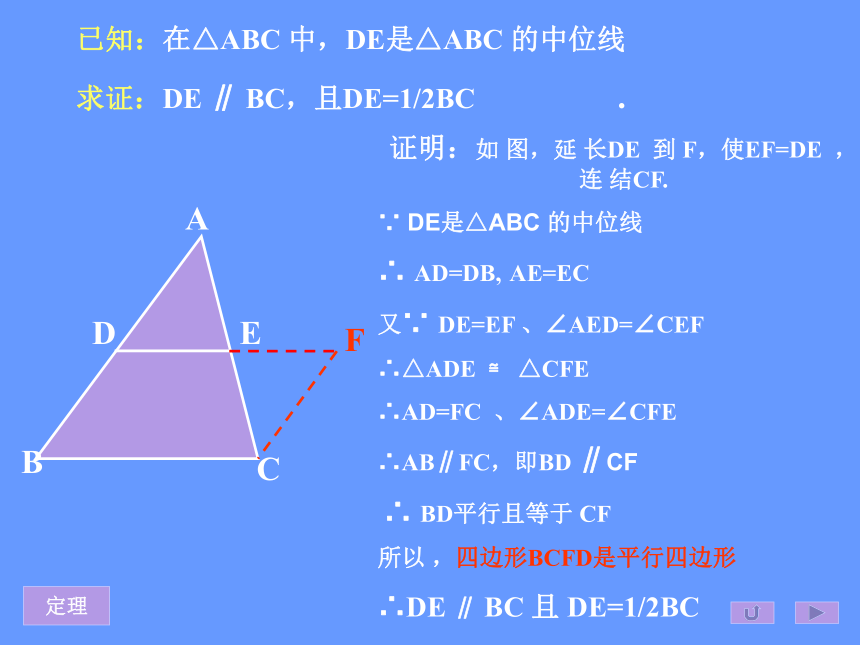
求证:DE ∥ BC,且DE=1/2BC . 证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.
∵ DE是△ABC 的中位线
∴ AD=DB, AE=EC
又∵ DE=EF 、∠AED=∠CEF
∴△ADE ≌ △CFE
∴AD=FC 、∠ADE=∠CFE
∴AB∥FC,即BD ∥CF
∴ BD平行且等于 CF
所以 ,四边形BCFD是平行四边形
∴DE ∥ BC 且 DE=1/2BC
定理
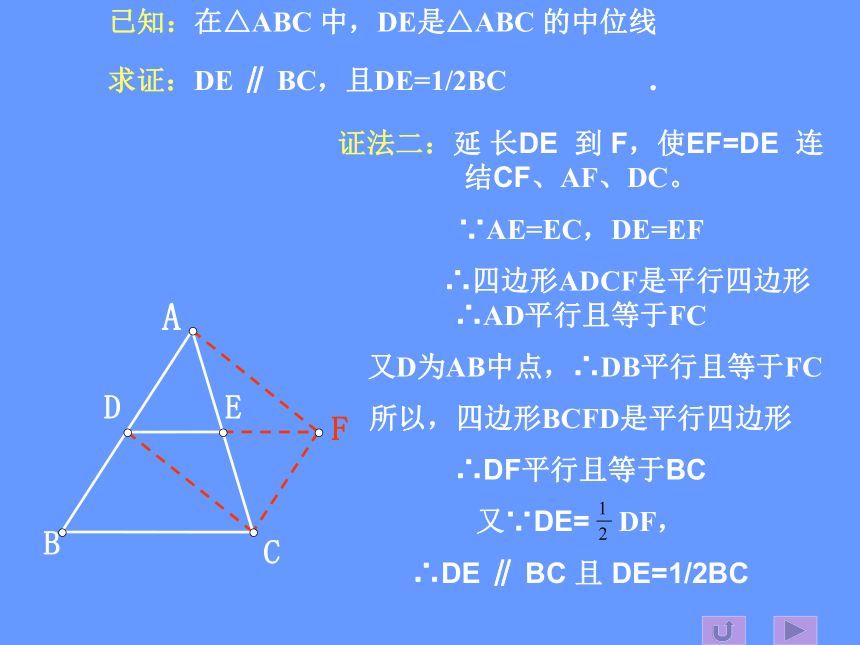
证法二:延 长DE 到 F,使EF=DE 连 结CF、AF、DC。
∵AE=EC,DE=EF
∴四边形ADCF是平行四边形∴AD平行且等于FC
又D为AB中点,∴DB平行且等于FC
所以,四边形BCFD是平行四边形
∴DF平行且等于BC
又∵DE=? DF,
∴DE ∥ BC 且 DE=1/2BC
ABCEDF已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE=1/2BC . 三角形中位线定理三角形的中位线平行于第三边,并且等于第三边的一半。如果 DE是△ABC的中位线
那么 ⑴ DE∥BC,
⑵ DE=1/2BC① 证明平行问题
② 证明一条线段是另一条线段的2倍或1/2用 途ABCDE1.如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么? 2.如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm图1图260412ABCD。。EBACD 。。E。F543A 。。BC 。D。。
E4. 在A、B外选一点C,连结AC和BC,并分别找出
AC和BC的中点D、E,如果能测量出DE的长度,
也就能知道AB的距离了。为什么?如果测的DE
=20m,那么A、B两点间的距离是多少?为什么?
2040随着学习的不断深入,同学们将会有更多的办法来解决这个问题1. 如图,AF=FD=DB,AG=GB=EC,FG∥DE∥BC,PE=1.5,则BC= ———34.59小 结三角形中位线定义三角形中位线定理三角形中位线定理应用END三角形的中位线是连结三角形两边中点的线段三角形的中线是连结一个顶点和它的对边中点的线段①三角形的中位线是三角形中一种重要的线段,它与三角形的中线不同:②理解三角形的中位线定义的两层含义:⑵∵ DE为△ABC的中位线 ⑴∵D、E分别为AB、AC的中点 ∴DE为△ABC的中位线∴ D、E分别为AB、AC的中点③一个三角形共有三条中位线。定义 如果 DE是△ABC的中位线
那么 ⑴ DE∥BC,
⑵ DE=1/2BC① 证明平行
② 证明一条线段是另一条线段的2倍或1/2ABCDE 三角形的中位线定理 是三 角形 的一个重要性质定理:
三角形的中位线平行于第三边,并且等于第三边的 一半.
.
定理的主要用途:例1例1.求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形求证:四边形EFGH是平行四边形证明:连结AC∵AH=HD CG=GD∴HG∥AC(三角形的中位线平行于第三边,并且等于它的一半)同理EF∥AC∴HG∥EF且HG=EF∴四边形EFGH是平行四边形
A 。。BC 。D。。
E如图,在A、B外选一点C,连结AC和BC,A、B两点被池塘隔开,现在要测量出A、B两点间的距离 ,但又无法直接去测量,怎么办?这堂课,我们将教大家一种测量的方法。并分别找出AC和BC的中点D、E,如果能测量出DE的长度,也就能知道AB的距离了。今天这堂课我们就要来探究其中的学问。
三角形的中位线和三角形的中线
不同CBAFED定义:连接三角形两边中点的线段
叫做三角形的中位线
AF是△ABC的中线我们把DE叫△ ABC 的中位线 注意:三角形的中位线是连结三角形两边中点的线段三角形的中线是连结一个顶点和它的对边中点的线段 区分三角形的中位线和中线: 理解三角形的中位线定义的两层含义:② ∵ DE为△ABC的中位线 ① ∵D、E分别为AB、AC的中点 ∴DE为△ABC的中位线∴ D、E分别为AB、AC的中点 一个三角形共有三条中位线。定义ABCD。。E。FABCDEF已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE=1/2BC . 证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.
∵ DE是△ABC 的中位线
∴ AD=DB, AE=EC
又∵ DE=EF 、∠AED=∠CEF
∴△ADE ≌ △CFE
∴AD=FC 、∠ADE=∠CFE
∴AB∥FC,即BD ∥CF
∴ BD平行且等于 CF
所以 ,四边形BCFD是平行四边形
∴DE ∥ BC 且 DE=1/2BC
定理
证法二:延 长DE 到 F,使EF=DE 连 结CF、AF、DC。
∵AE=EC,DE=EF
∴四边形ADCF是平行四边形∴AD平行且等于FC
又D为AB中点,∴DB平行且等于FC
所以,四边形BCFD是平行四边形
∴DF平行且等于BC
又∵DE=? DF,
∴DE ∥ BC 且 DE=1/2BC
ABCEDF已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE=1/2BC . 三角形中位线定理三角形的中位线平行于第三边,并且等于第三边的一半。如果 DE是△ABC的中位线
那么 ⑴ DE∥BC,
⑵ DE=1/2BC① 证明平行问题
② 证明一条线段是另一条线段的2倍或1/2用 途ABCDE1.如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么? 2.如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm图1图260412ABCD。。EBACD 。。E。F543A 。。BC 。D。。
E4. 在A、B外选一点C,连结AC和BC,并分别找出
AC和BC的中点D、E,如果能测量出DE的长度,
也就能知道AB的距离了。为什么?如果测的DE
=20m,那么A、B两点间的距离是多少?为什么?
2040随着学习的不断深入,同学们将会有更多的办法来解决这个问题1. 如图,AF=FD=DB,AG=GB=EC,FG∥DE∥BC,PE=1.5,则BC= ———34.59小 结三角形中位线定义三角形中位线定理三角形中位线定理应用END三角形的中位线是连结三角形两边中点的线段三角形的中线是连结一个顶点和它的对边中点的线段①三角形的中位线是三角形中一种重要的线段,它与三角形的中线不同:②理解三角形的中位线定义的两层含义:⑵∵ DE为△ABC的中位线 ⑴∵D、E分别为AB、AC的中点 ∴DE为△ABC的中位线∴ D、E分别为AB、AC的中点③一个三角形共有三条中位线。定义 如果 DE是△ABC的中位线
那么 ⑴ DE∥BC,
⑵ DE=1/2BC① 证明平行
② 证明一条线段是另一条线段的2倍或1/2ABCDE 三角形的中位线定理 是三 角形 的一个重要性质定理:
三角形的中位线平行于第三边,并且等于第三边的 一半.
.
定理的主要用途:例1例1.求证:顺次连结四边形四条边的中点,所得的四边形是平行四边形求证:四边形EFGH是平行四边形证明:连结AC∵AH=HD CG=GD∴HG∥AC(三角形的中位线平行于第三边,并且等于它的一半)同理EF∥AC∴HG∥EF且HG=EF∴四边形EFGH是平行四边形
