湖南省永州市绍基学校2023学年湘教版八年级上册数学第二章 三角形 检测试题(无答案)
文档属性
| 名称 | 湖南省永州市绍基学校2023学年湘教版八年级上册数学第二章 三角形 检测试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 471.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-01 08:47:59 | ||
图片预览


文档简介
绍基学校2023年八年级上数学第二章检测试题(一)
一.选择题(每小题3分,共30分)
1.如图,已知,,,则的度数为( )
A. B. C. D.
2.在如图所示的图形中,三角形的个数为( )
A.3 B.4 C.5 D.6
3.在中,若,则是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
4.下列说法中错误的是( )
A.三角形的三个内角中至少有两个角是锐角
B.有一个角是锐角的三角形是锐角三角形
C.一个三角形的三个内角中至少有一个内角不大于
D.如果三角形的两个内角之和小于,那么这个三角形是钝角三角形
5.如图,盖房子时,在窗框没有安装之前,木工师傅常常先在窗框上斜钉一根木条让其固定,其所运用的几何原理是( )
A.三角形的稳定性 B.垂线段最短
C.两点确定一条直线 D.两点之间,线段最短
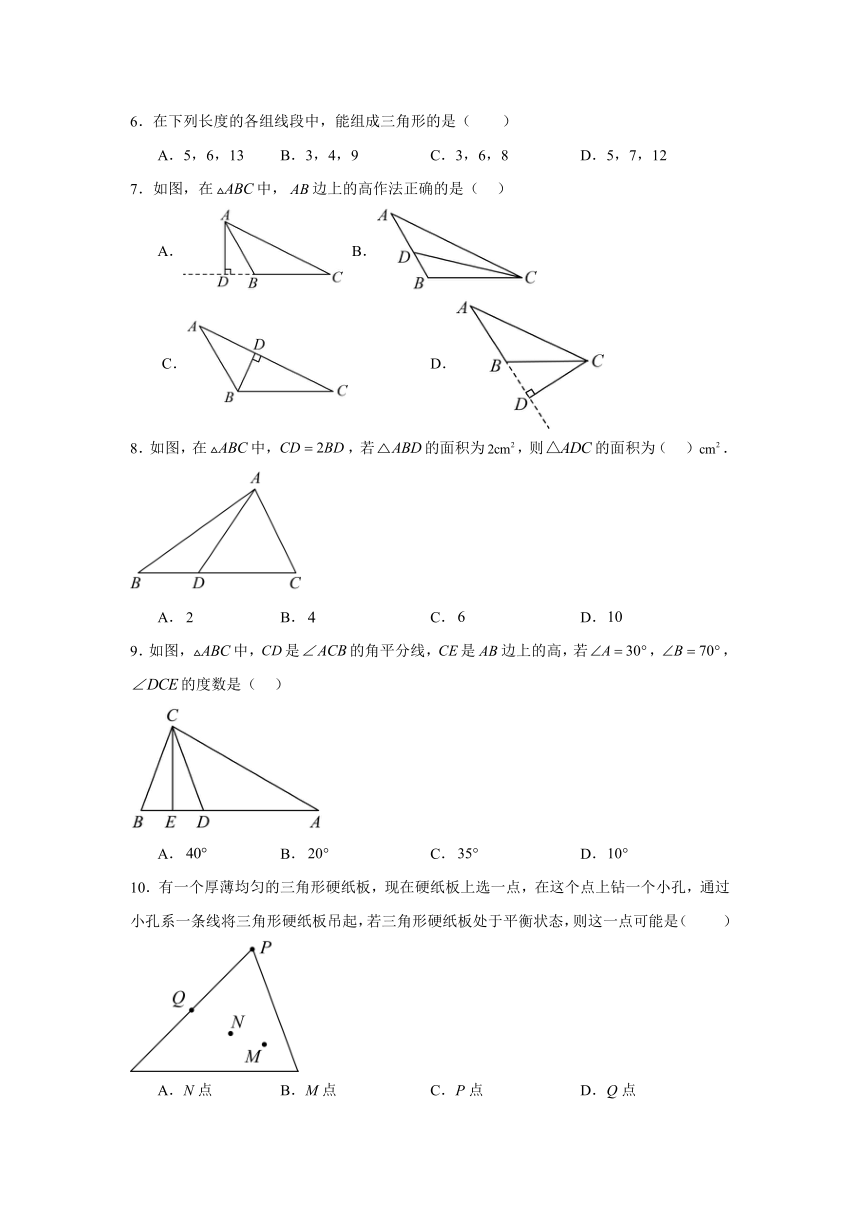
6.在下列长度的各组线段中,能组成三角形的是( )
A.5,6,13 B.3,4,9 C.3,6,8 D.5,7,12
7.如图,在中,边上的高作法正确的是( )
A. B.
C. D.
8.如图,在中,,若的面积为,则的面积为( ).
A. B. C. D.
9.如图,中,是的角平分线,是边上的高,若,,的度数是( )
A. B. C. D.
10.有一个厚薄均匀的三角形硬纸板,现在硬纸板上选一点,在这个点上钻一个小孔,通过小孔系一条线将三角形硬纸板吊起,若三角形硬纸板处于平衡状态,则这一点可能是( )
A.N点 B.M点 C.P点 D.Q点
二.填空题(每小题3分,共18分)
11.一个三角形的周长为81cm,三边长的比为,则最长边是 .
12.,垂足为.BD=DC,以为中线的三角形是 ;以为高线的三角形有 个.
13.如图,和分别是的中线和高,且,,则=
14.如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是 .
15.如图,在中,点D、E分别为边、上的点,连接,将沿翻折得到,使.若,,则的大小为 .
16.如图,在中E是上的一点,,点D是的中点,与相交于点F,设,,的面积分别为,,,且,则 .
三.解答题(共72分)
17.(9分)如果一个三角形的一边长为,另一边长为,若第三边长为.
(1)第三边的范围为______.
(2)当第三边长为奇数时,求出这个三角形的周长,并指出它是什么三角形(按边分类).
18.(12分)在正方形网格中,每个小正方形的边长均为1个单位长度,的三个顶点的位置如图所示.现将平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的.
(2)画出的边上的高.
(3)画出边上的中线.
(4)若连接、,则这两条线段之间的关系是______.
19.(6分)如图,在中,,,为的平分线,,垂足为,求的度数.
20.(6分)如图,在中,是的平分线,且,.
(1)求各内角的度数;
(2)求的度数.
21.(9分)常用的分解因式方法有提取公因式法、公式法等,但有的多项式只用上述方法就无法分解,细心观察这个公式发现,前两项符合平方差公式,分解因式后产生公因式,然后提取公因式就可以完成整个式子的分解因式;过程如下:
这种分解因式的方法叫做分组分解法,利用这种方法解决下列问题:
(1)试用“分组分解法”分解因式:;
(2)三边满足,判断的形状.
(3)已知,求a+b的值.
22.(10分)如图,已知,点分别在上,,.
(1)求证:;
(2)求证:.
23.(10分)已知:如图,在中,是边上的中线.
求证:(填空).
证明:在三角形中,
∵,
∴ ( ).
∴= (全等三角形的对应角相等).
∴(平角的意义).
∴ (垂直的意义).
24.(10分)如图,在和中,,,,连接.
(1)求证:.
(2)图中和有怎样的关系?试证明你的结论.
一.选择题(每小题3分,共30分)
1.如图,已知,,,则的度数为( )
A. B. C. D.
2.在如图所示的图形中,三角形的个数为( )
A.3 B.4 C.5 D.6
3.在中,若,则是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
4.下列说法中错误的是( )
A.三角形的三个内角中至少有两个角是锐角
B.有一个角是锐角的三角形是锐角三角形
C.一个三角形的三个内角中至少有一个内角不大于
D.如果三角形的两个内角之和小于,那么这个三角形是钝角三角形
5.如图,盖房子时,在窗框没有安装之前,木工师傅常常先在窗框上斜钉一根木条让其固定,其所运用的几何原理是( )
A.三角形的稳定性 B.垂线段最短
C.两点确定一条直线 D.两点之间,线段最短
6.在下列长度的各组线段中,能组成三角形的是( )
A.5,6,13 B.3,4,9 C.3,6,8 D.5,7,12
7.如图,在中,边上的高作法正确的是( )
A. B.
C. D.
8.如图,在中,,若的面积为,则的面积为( ).
A. B. C. D.
9.如图,中,是的角平分线,是边上的高,若,,的度数是( )
A. B. C. D.
10.有一个厚薄均匀的三角形硬纸板,现在硬纸板上选一点,在这个点上钻一个小孔,通过小孔系一条线将三角形硬纸板吊起,若三角形硬纸板处于平衡状态,则这一点可能是( )
A.N点 B.M点 C.P点 D.Q点
二.填空题(每小题3分,共18分)
11.一个三角形的周长为81cm,三边长的比为,则最长边是 .
12.,垂足为.BD=DC,以为中线的三角形是 ;以为高线的三角形有 个.
13.如图,和分别是的中线和高,且,,则=
14.如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是 .
15.如图,在中,点D、E分别为边、上的点,连接,将沿翻折得到,使.若,,则的大小为 .
16.如图,在中E是上的一点,,点D是的中点,与相交于点F,设,,的面积分别为,,,且,则 .
三.解答题(共72分)
17.(9分)如果一个三角形的一边长为,另一边长为,若第三边长为.
(1)第三边的范围为______.
(2)当第三边长为奇数时,求出这个三角形的周长,并指出它是什么三角形(按边分类).
18.(12分)在正方形网格中,每个小正方形的边长均为1个单位长度,的三个顶点的位置如图所示.现将平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的.
(2)画出的边上的高.
(3)画出边上的中线.
(4)若连接、,则这两条线段之间的关系是______.
19.(6分)如图,在中,,,为的平分线,,垂足为,求的度数.
20.(6分)如图,在中,是的平分线,且,.
(1)求各内角的度数;
(2)求的度数.
21.(9分)常用的分解因式方法有提取公因式法、公式法等,但有的多项式只用上述方法就无法分解,细心观察这个公式发现,前两项符合平方差公式,分解因式后产生公因式,然后提取公因式就可以完成整个式子的分解因式;过程如下:
这种分解因式的方法叫做分组分解法,利用这种方法解决下列问题:
(1)试用“分组分解法”分解因式:;
(2)三边满足,判断的形状.
(3)已知,求a+b的值.
22.(10分)如图,已知,点分别在上,,.
(1)求证:;
(2)求证:.
23.(10分)已知:如图,在中,是边上的中线.
求证:(填空).
证明:在三角形中,
∵,
∴ ( ).
∴= (全等三角形的对应角相等).
∴(平角的意义).
∴ (垂直的意义).
24.(10分)如图,在和中,,,,连接.
(1)求证:.
(2)图中和有怎样的关系?试证明你的结论.
同课章节目录
