能得到直角三角形吗[下学期]
文档属性
| 名称 | 能得到直角三角形吗[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 13.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-19 22:30:00 | ||
图片预览





文档简介
课件12张PPT。18.2勾股定理的逆定理学习目标
1、理解掌握勾股定理的逆定理。
2、了解原命题逆命题以及原定理逆定理的含义。
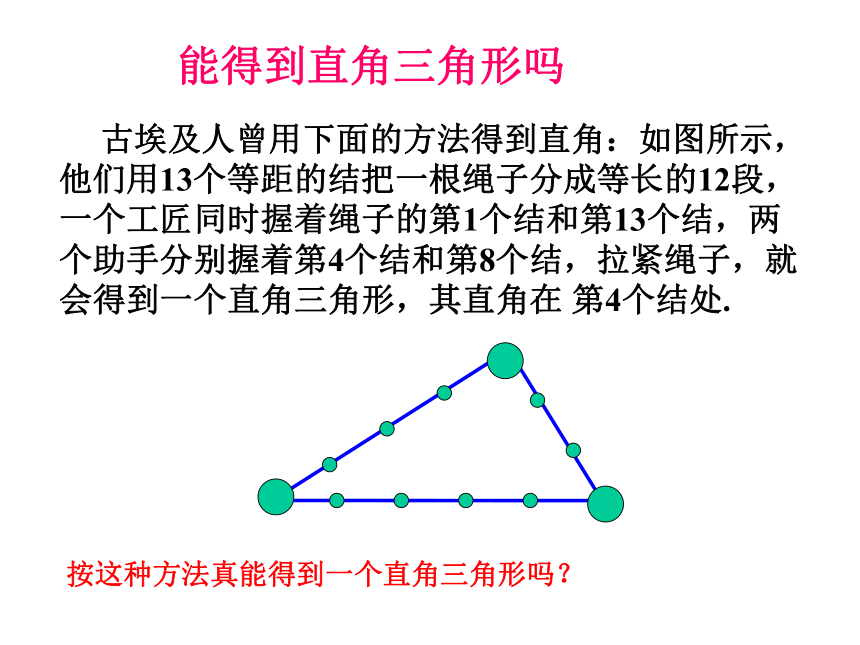
3、会简单运用勾股定理的逆定理。 古埃及人曾用下面的方法得到直角:如图所示,他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握着绳子的第1个结和第13个结,两个助手分别握着第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在 第4个结处.按这种方法真能得到一个直角三角形吗? 能得到直角三角形吗自学指导
认真阅读教材81~82页,时间4分钟,
要求:
1、理解掌握勾股定理的逆定理。
2、了解原命题逆命题以及原定理逆定理的含义。
3、会简单运用勾股定理的逆定理。
做一做:
下面的三组数分别是一个三角形的三边长a,b,c:
5,12,13; 6, 8, 10; 8,15,17.(1)这三组数都满足a2 +b2=c2吗?(2)分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形
满足a2 +b2=c2的三个正整数,称为勾股数勾股定理的逆定理在?ABC中, a,b,c为三边长,其中 c为最大边,
若a2 +b2=c2, 则?ABC为直角三角形;
若a2 +b2>c2, 则?ABC为锐角三角形;
若a2 +b23:4:7; B. 5:12:13; C. 1:2:4; D. 1:3:5.将直角三角形的三边的长度扩大同样的倍数,则得到的三角形是 ( )
是直角三角形; B. 可能是锐角三角形;
C. 可能是钝角三角形; D. 不可能是直角三角形.BA三角形的三边分别是a,b,c, 且满足等式(a+b)2-c2=2ab, 则此三角形是: ( )
A. 直角三角形; B. 是锐角三角形;
是钝角三角形; D. 是等腰直角三角形.已知?ABC中BC=41, AC=40, AB=9, 则此三角形为_______三角形, ______是最大角.5. 以?ABC的三条边为边长向外作正方形, 依次得到的面积是25, 144 , 169, 则这个三角形是______三角形.A直角直角∠ A四边形ABCD中已知AB=3, BC=4, CD=12, DA=13, 且∠ABC=900,求这个四边形的面积.7、请你写出三组勾股数;
8、一组勾股数的倍数一定是勾股数吗?为什么?小结:
勾股定理的逆定理:
如果三角形的三边长a,b,c满足a2 +b2=c2,
那么这个三角形是直角三角形
勾股数:
满足a2 +b2=c2的三个正整数,称为勾股数
作业:P12的习题1.3及P17A组的2,3,4题以及补充练习中没做完的题
补充思考题: △ABC中,AB=17cm, BC=30cm, BC上中线AD=8cm,请你判断△ABC的形状,并说明理由。
1、理解掌握勾股定理的逆定理。
2、了解原命题逆命题以及原定理逆定理的含义。
3、会简单运用勾股定理的逆定理。 古埃及人曾用下面的方法得到直角:如图所示,他们用13个等距的结把一根绳子分成等长的12段,一个工匠同时握着绳子的第1个结和第13个结,两个助手分别握着第4个结和第8个结,拉紧绳子,就会得到一个直角三角形,其直角在 第4个结处.按这种方法真能得到一个直角三角形吗? 能得到直角三角形吗自学指导
认真阅读教材81~82页,时间4分钟,
要求:
1、理解掌握勾股定理的逆定理。
2、了解原命题逆命题以及原定理逆定理的含义。
3、会简单运用勾股定理的逆定理。
做一做:
下面的三组数分别是一个三角形的三边长a,b,c:
5,12,13; 6, 8, 10; 8,15,17.(1)这三组数都满足a2 +b2=c2吗?(2)分别以每组数为三边长作出三角形,用量角器量一量,它们都是直角三角形吗?
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形
满足a2 +b2=c2的三个正整数,称为勾股数勾股定理的逆定理在?ABC中, a,b,c为三边长,其中 c为最大边,
若a2 +b2=c2, 则?ABC为直角三角形;
若a2 +b2>c2, 则?ABC为锐角三角形;
若a2 +b2
是直角三角形; B. 可能是锐角三角形;
C. 可能是钝角三角形; D. 不可能是直角三角形.BA三角形的三边分别是a,b,c, 且满足等式(a+b)2-c2=2ab, 则此三角形是: ( )
A. 直角三角形; B. 是锐角三角形;
是钝角三角形; D. 是等腰直角三角形.已知?ABC中BC=41, AC=40, AB=9, 则此三角形为_______三角形, ______是最大角.5. 以?ABC的三条边为边长向外作正方形, 依次得到的面积是25, 144 , 169, 则这个三角形是______三角形.A直角直角∠ A四边形ABCD中已知AB=3, BC=4, CD=12, DA=13, 且∠ABC=900,求这个四边形的面积.7、请你写出三组勾股数;
8、一组勾股数的倍数一定是勾股数吗?为什么?小结:
勾股定理的逆定理:
如果三角形的三边长a,b,c满足a2 +b2=c2,
那么这个三角形是直角三角形
勾股数:
满足a2 +b2=c2的三个正整数,称为勾股数
作业:P12的习题1.3及P17A组的2,3,4题以及补充练习中没做完的题
补充思考题: △ABC中,AB=17cm, BC=30cm, BC上中线AD=8cm,请你判断△ABC的形状,并说明理由。
