数学人教A版(2019)必修第一册5.4.1正弦函数、余弦函数的图象(共30张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.4.1正弦函数、余弦函数的图象(共30张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-01 19:09:31 | ||
图片预览





文档简介
(共30张PPT)
第五章 三角函数
5.4.1 正弦函数、余弦函数的图象
高中数学/人教A版/必修一
三角函数定义
1
复习回顾
α的终边
P(x,y)
O
x
y
·
o1
x
y
o
-1
1
1.如何利用三角函数定义画出函数 的
图象?
2
正弦函数图象
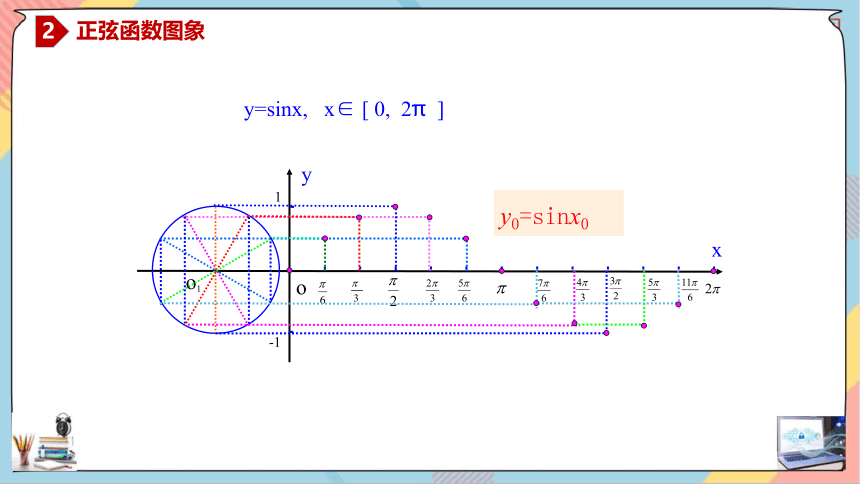
y0=sinx0
y=sinx, x∈ [ 0, 2π ]
o1
o
1
x
y
-1
2
正弦函数图象
y0=sinx0
o1
o
1
x
y
-1
2
正弦函数图象
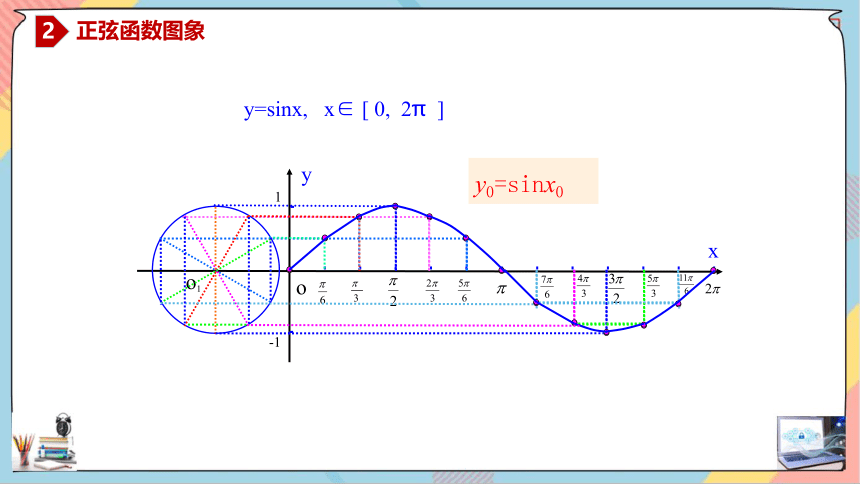
y0=sinx0
y=sinx, x∈ [ 0, 2π ]
2.如何得到正弦函数 的图象呢?
2
正弦函数图象
公式一:
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
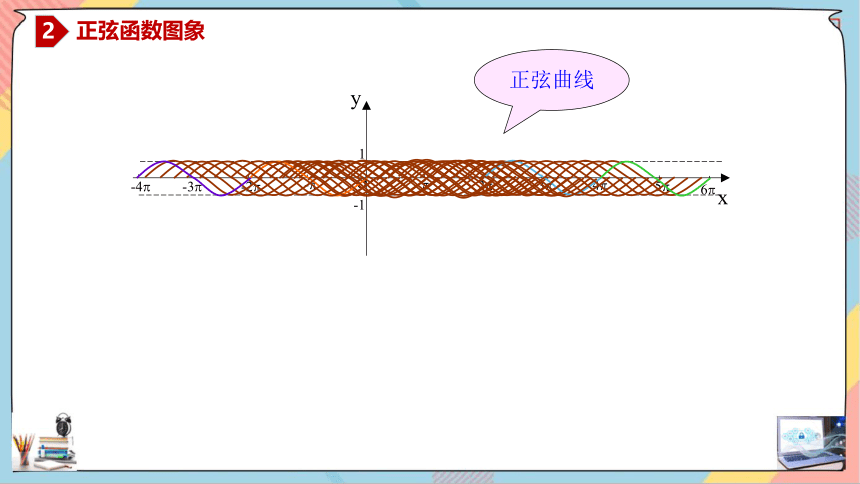
正弦曲线
2
正弦函数图象
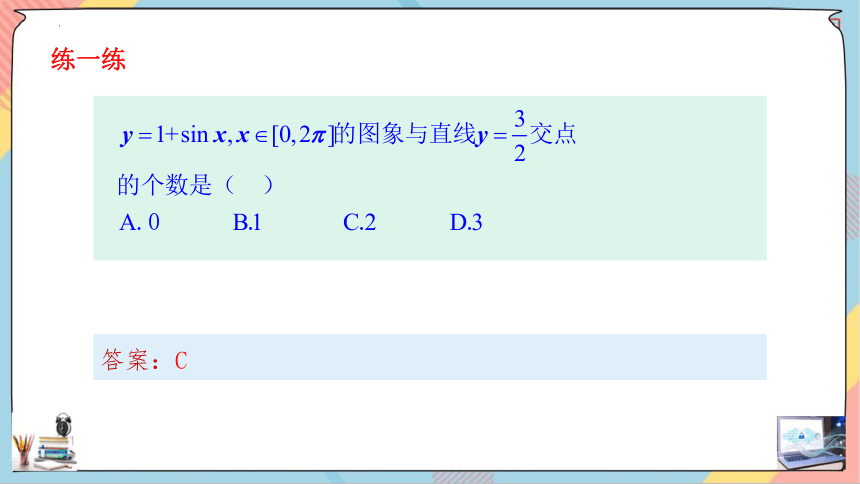
练一练
答案:C
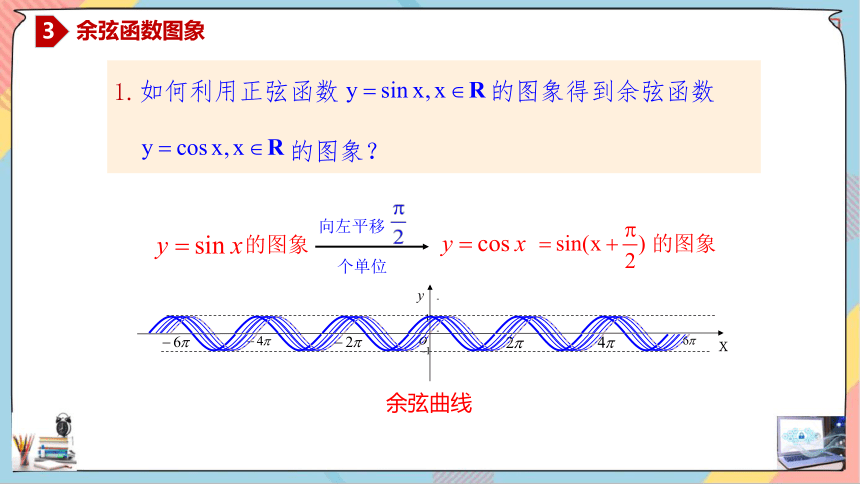
1.如何利用正弦函数 的图象得到余弦函数
的图象?
的图象
的图象
向左平移
个单位
余弦曲线
-
-
1
-1
x
3
余弦函数图象
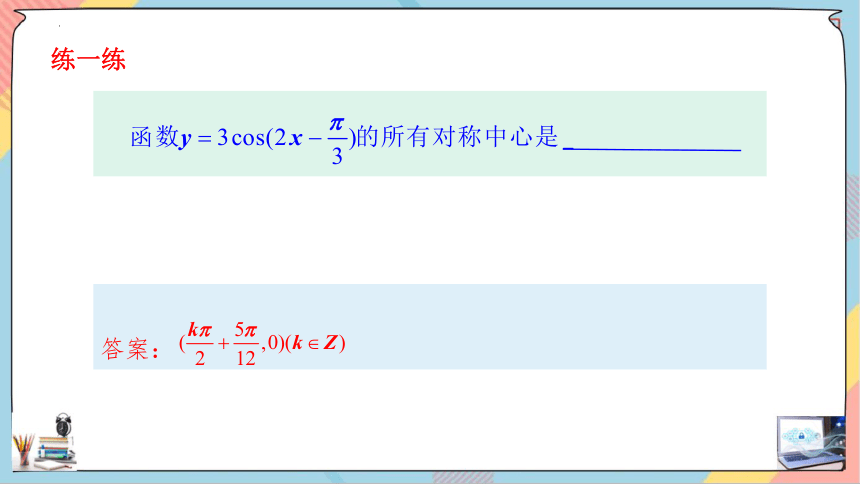
答案:
练一练
-
-
-1
1
-
-1
1. 在作正弦函数的图象时,应抓住哪些关键点?
与x轴的交点
图象的最高点
图象的最低点
(0,0)
4
五点作图法
-
-
-1
1
-
-1
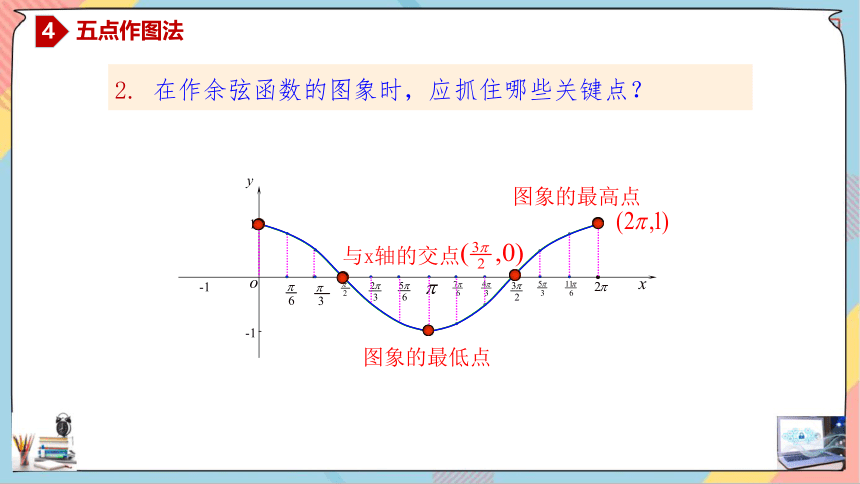
2. 在作余弦函数的图象时,应抓住哪些关键点?
与x轴的交点
图象的最高点
图象的最低点
4
五点作图法
3. 通过上面的分析,你能不能更快捷地画出正弦函数
和余弦函数的简图?如何画?
五点作图法:
(1) 列表(列出对图象形状起关键作用的五点坐标).
(2) 描点(定出五个关键点).
(3) 连线(用光滑的曲线顺次连接五个点).
4
五点作图法
在同一坐标系内,用五点法分别画出函数
y=sinx,x [0, 2 ] 和 y=cosx,x [ , ]的简图,并观察两条曲线,说出它们的关系.
练一练
x
sinx
0
1
0
0
o
1
y
x
-1
2
y=sinx,x [0, 2 ]
y= cosx,x [ , ]
向左平移 个单位长度
0 2
x
cosx
解:
0
1
0
0
-1
0
x
sinx
1+sinx
(1)y=1+sinx , x∈[0,2π];(2)y=-cosx, x∈[0,2π].
例.画出下列函数的简图:
解:(1)按五个关键点列表:
0
0
0
0
1
-1
1
1
2
0
1
5
典型例题
x
-1
O
2π
π
1
y
2
y=1+sinx,x∈[0,2π]
描点并将它们用光滑的曲线连接起来:
描点法作图的一般步骤:列表、描点、连线
y=sinx,x∈[0,2π]
解:(2)按五个关键点列表:
0
1
-1
1
0
0
1
-1
0
0
-1
x
cosx
-cosx
x
-1
O
2π
π
1
y
y=-cosx,x∈[0,2π]
描点并将它们用光滑的曲线连接起来:
y=cosx,x∈[0,2π]
1.分别作出下列函数简图(五点法作图).
(1)y=2sinx , x∈[0,2π];
(2)y=sin2x , x∈[0,π].
练一练
列表
②描点作图
解:(1)y=2sinx , x∈[0,2π]
①
x
0 2
0 2 0 -2 0
y
2
x
O
y=2sinx,x∈[0,2π]
y=2sinx
1
-1
-2
列表
②描点作图
解:(2)y=sin2x , x∈[0,π]
①
x 0
0 2
2x
0 1 0 -1 0
y
1
O
y=sin2x,x∈[0,π]
y=sin2x
-1
① ④
练一练
D
练一练
C
练一练
B
练一练
课堂小结
一、本节课学习的新知识
正弦函数图象
余弦函数图象
五点作图法
二、本节课提升的核心素养
数据分析
课堂小结
直观想象
数学运算
逻辑推理
三、本节课训练的数学思想方法
数形结合
课堂小结
转化与化归
类比思想
01
基础作业: .
02
能力作业: .
03
拓展延伸:(选做)
作业
第五章 三角函数
5.4.1 正弦函数、余弦函数的图象
高中数学/人教A版/必修一
三角函数定义
1
复习回顾
α的终边
P(x,y)
O
x
y
·
o1
x
y
o
-1
1
1.如何利用三角函数定义画出函数 的
图象?
2
正弦函数图象
y0=sinx0
y=sinx, x∈ [ 0, 2π ]
o1
o
1
x
y
-1
2
正弦函数图象
y0=sinx0
o1
o
1
x
y
-1
2
正弦函数图象
y0=sinx0
y=sinx, x∈ [ 0, 2π ]
2.如何得到正弦函数 的图象呢?
2
正弦函数图象
公式一:
x
6
y
o
-
-1
2
3
4
5
-2
-3
-4
1
正弦曲线
2
正弦函数图象
练一练
答案:C
1.如何利用正弦函数 的图象得到余弦函数
的图象?
的图象
的图象
向左平移
个单位
余弦曲线
-
-
1
-1
x
3
余弦函数图象
答案:
练一练
-
-
-1
1
-
-1
1. 在作正弦函数的图象时,应抓住哪些关键点?
与x轴的交点
图象的最高点
图象的最低点
(0,0)
4
五点作图法
-
-
-1
1
-
-1
2. 在作余弦函数的图象时,应抓住哪些关键点?
与x轴的交点
图象的最高点
图象的最低点
4
五点作图法
3. 通过上面的分析,你能不能更快捷地画出正弦函数
和余弦函数的简图?如何画?
五点作图法:
(1) 列表(列出对图象形状起关键作用的五点坐标).
(2) 描点(定出五个关键点).
(3) 连线(用光滑的曲线顺次连接五个点).
4
五点作图法
在同一坐标系内,用五点法分别画出函数
y=sinx,x [0, 2 ] 和 y=cosx,x [ , ]的简图,并观察两条曲线,说出它们的关系.
练一练
x
sinx
0
1
0
0
o
1
y
x
-1
2
y=sinx,x [0, 2 ]
y= cosx,x [ , ]
向左平移 个单位长度
0 2
x
cosx
解:
0
1
0
0
-1
0
x
sinx
1+sinx
(1)y=1+sinx , x∈[0,2π];(2)y=-cosx, x∈[0,2π].
例.画出下列函数的简图:
解:(1)按五个关键点列表:
0
0
0
0
1
-1
1
1
2
0
1
5
典型例题
x
-1
O
2π
π
1
y
2
y=1+sinx,x∈[0,2π]
描点并将它们用光滑的曲线连接起来:
描点法作图的一般步骤:列表、描点、连线
y=sinx,x∈[0,2π]
解:(2)按五个关键点列表:
0
1
-1
1
0
0
1
-1
0
0
-1
x
cosx
-cosx
x
-1
O
2π
π
1
y
y=-cosx,x∈[0,2π]
描点并将它们用光滑的曲线连接起来:
y=cosx,x∈[0,2π]
1.分别作出下列函数简图(五点法作图).
(1)y=2sinx , x∈[0,2π];
(2)y=sin2x , x∈[0,π].
练一练
列表
②描点作图
解:(1)y=2sinx , x∈[0,2π]
①
x
0 2
0 2 0 -2 0
y
2
x
O
y=2sinx,x∈[0,2π]
y=2sinx
1
-1
-2
列表
②描点作图
解:(2)y=sin2x , x∈[0,π]
①
x 0
0 2
2x
0 1 0 -1 0
y
1
O
y=sin2x,x∈[0,π]
y=sin2x
-1
① ④
练一练
D
练一练
C
练一练
B
练一练
课堂小结
一、本节课学习的新知识
正弦函数图象
余弦函数图象
五点作图法
二、本节课提升的核心素养
数据分析
课堂小结
直观想象
数学运算
逻辑推理
三、本节课训练的数学思想方法
数形结合
课堂小结
转化与化归
类比思想
01
基础作业: .
02
能力作业: .
03
拓展延伸:(选做)
作业
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
