数学人教A版(2019)选择性必修第一册2.5.2圆与圆的位置关系(共33张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.5.2圆与圆的位置关系(共33张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-01 00:00:00 | ||
图片预览










文档简介
(共33张PPT)
2.5.2 圆与圆的位置关系
选择性必修第一册 第二章《直线和圆的方程》
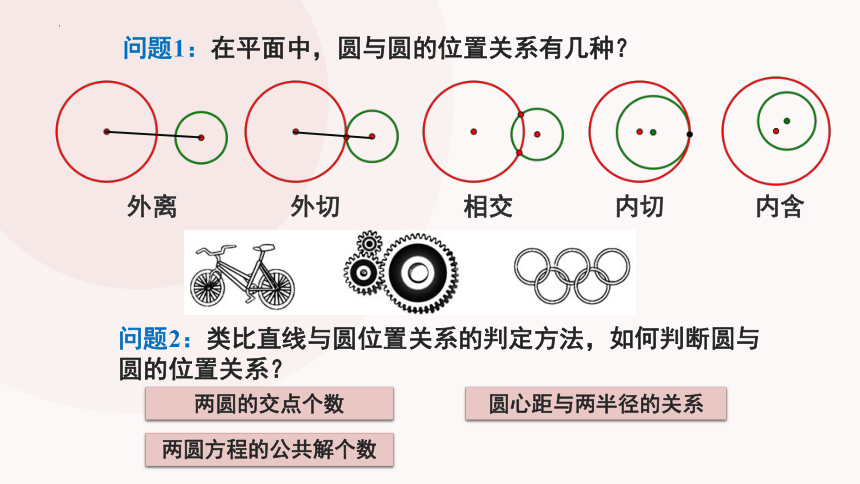
问题1:在平面中,圆与圆的位置关系有几种?
问题2:类比直线与圆位置关系的判定方法,如何判断圆与圆的位置关系?
两圆的交点个数
圆心距与两半径的关系
两圆方程的公共解个数
外离
相交
内含
外切
内切
新知1:圆与圆位置关系的判定
圆与圆的位置关系 外离 外切 相交 内切 内含
图示
两圆交点个数 0个 1个 2个 1个 0个
几何法:圆心距d与R±r的关系
代数法:联立两圆方程,消元所得方程解的个数(△的正负)
当Δ=0或Δ<0时,不能确定两圆的位置关系
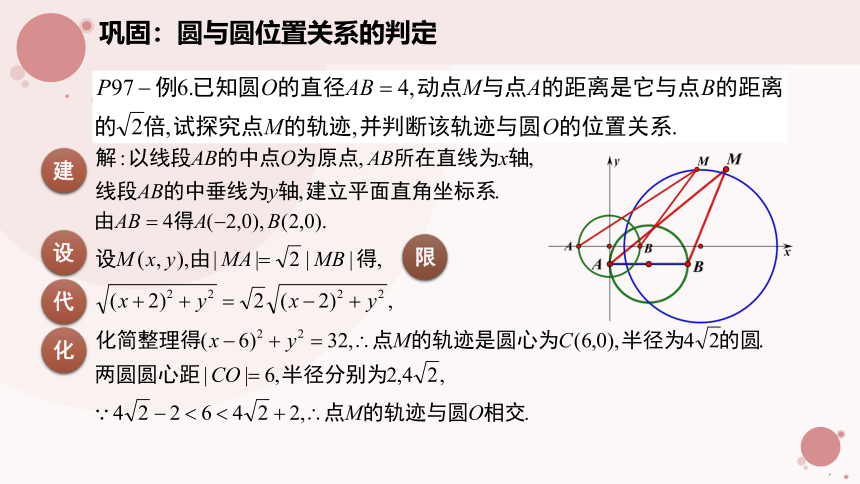
巩固:圆与圆位置关系的判定
外切或内切
巩固:圆与圆位置关系的判定
建
设
限
代
化
新知2:两圆的公共弦
1.公共弦的定义:两圆相交时两个交点的连线;
2.公共弦的性质:相交两圆的连心线垂直平分其公共弦。
练习2.已知两圆相交于两点A(1,3)和B(m,-1),且两圆圆心都在直线x-y+c=0上,,则m+c的值为 .
新知2:两圆的公共弦
3.求两圆公共弦所在直线方程:
法2:两圆方程作差
法1:联立两圆方程求交点,由两点求直线方程
新知2:两圆的公共弦
3.求两圆公共弦所在直线方程:
法2:两圆方程作差
[注]①当两圆方程中二次项系数相同时,才能作差求解,否则应先化同系数.
②两圆相切时,(*)表示过切点且垂直于连心线的切线方程;
③两圆外离或内含时,(*)表示垂直于连心线的直线方程;
法1:联立两圆方程求交点,由两点求直线方程
4.求两圆公共弦长:
法1:联立两圆方程求交点,求两点距离
法2:求公共弦所在直线方程+垂径定理
典例详解:圆与圆位置关系的判定及公共弦问题
典例详解:圆与圆位置关系的判定及公共弦问题
相交
综合巩固——公共弦问题
【结论】若圆的一条直径的端点分别是A(x ,y ),B(x ,y ),则此圆的方程是(x-x )(x-x )+(y-y1)(y-y )=0.
解:(2)直线PA,PB是圆Q的切线.
因为点A,B在圆 上,且PQ是直径,
所以PA⊥AQ,PB⊥BQ ,所以直线PA,PB是圆Q的切线.
(3)将两圆方程 ,
相减,得6x+5y-25=0,即直线AB的方程是6x+5y-25=0.
小结:两圆的公共弦问题
1.公共弦的性质:相交两圆的连心线垂直平分其公共弦。
2.求两圆公共弦所在直线方程:两圆方程作差
①两圆相切时,(*)表示过切点且垂直于连心线的切线方程;
②两圆外离或内含时,(*)表示垂直于连心线的直线方程;
3.求两圆公共弦长:
求公共弦所在直线方程+垂径定理
综合巩固——公共弦问题
练习2.两圆x2+y2+2ax+2ay+2a2-3=0与x2+y2+2bx+2by+2b2-1=0
公共弦长的最大值为( C ) A.0 B.1 C.2 D.3
综合巩固——公共弦问题
练习3.(多选)已知圆C1:x2+y2=r2,圆C2:(x-a)2+(y-b)2=r2(r>0)
交于不同的A(x1,y1),B(x2,y2)两点,下列结论正确的有( ABC )
A.a(x1-x2)+b(y1-y2)=0 B.2ax1+2by1=a2+b2
C.x1+x2=a D.y1+y2=2b
要点速览
圆系方程的结论及运用
两圆的公切线问题
圆上的点到定直线的距离为定值的点的个数
回顾:直线系方程
当λ(λ∈R)变化时,方程A1x+B1y+C1+λ(A2x+B2y+C2)=0表示过直线
l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0交点的直线束方程,但不包括直线l2.
(不包括直线2x-y+3=0)
(不包括直线x+3y-1=0)
问题:类比上述直线系方程的形式和推导过程,尝试写出过两圆交点的圆系方程.
新知3:圆系方程
当λ(λ∈R)变化时,方程A1x+B1y+C1+λ(A2x+B2y+C2)=0表示过直线
l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0交点的直线束方程,但不包括直线l2.
巩固应用:圆系方程
求圆心
求半径
巩固应用:圆系方程
P98-8.求圆心在x-y-4=0上,且过圆x2+y2+6x-4=0和圆x2+y2+6y-28=0的交点的圆的方程.
巩固应用:圆系方程
P98-7.求经过点M(2,-2)以及圆x2+y2-6x=0与圆x2+y2=4交点的圆的方程.
[变式]求过直线x+2y-3=0与圆x2+y2-2x=0的交点,且圆心在y轴上的圆方程.
巩固应用:圆系方程
P98-8.求圆心在x-y-4=0上,且过圆x2+y2+6x-4=0和圆x2+y2+6y-28=0的交点的圆方程.
新知4:圆的相切问题
和两个圆都相切的直线叫做这两个圆的公切线。
外公切线:两圆在公切线的同旁。
内公切线:两圆在公切线的两侧。
位置关系 图形 公切线条数
外离 4
外切 3
相交 2
内切 1
内含 0
练习1.圆C1:x2+y2-2x-6y+1=0与圆C2:x2+y2+4x+2y+1=0的公切线有(C)
A.1条 B.2条 C.3条 D.4条
练习2.平面直角坐标系中,点A(0,1)和点B(4,5)到直线l的距离分别为1和2,则符合条件的直线l的条数为( 4 )条
巩固运用:圆的相切问题
圆上的点到到定直线的距离为定值的点的个数
d=r+1:1个
0≤dr-1d>r+1:0个
d=r-1:3个
圆上的点到直线距离为a(a考虑圆心到直线距离d 与r ±a的关系
直线与圆的方程的应用
选择性必修第一册 第二章《直线和圆的方程》
实际运用
P93-例3.如图是某圆拱桥的一孔圆拱的示意图。该圆拱跨度AB=20m,拱高OP=4m,在建造时每隔4m需要用一个支柱支撑,求支柱A2P2的长度.
把点P2(–2, y)代入圆的方程,得y=3.86(负值舍去)
解:如图建立平面直角坐标系,圆心在y轴上。设圆心的坐标是C(0,b),圆的半径是r,
则圆的方程为x2+(y–b)2=r2
∴支柱A2P2的长度为3.86米.
用坐标法解决问题的“三步曲”
1、建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素(如:点、直线、圆),将平面几何问题转化为代数问题.
2、通过代数运算,解决代数问题
3、把代数运算结果“翻译”成几何结论
代数
几何
几何
建系
坐标法
实际运用
P95-1.赵州桥的跨度是37.4m,圆拱高约为7.2m,求这座圆拱桥的拱圆方程。
著名匠师李春设计建造,为石拱桥,又称安济桥,坐落在河北省赵县的洨河上。经过无数次洪水冲击、风吹雨打、冰雪风霜的侵蚀和8次地震的考验,却安然无恙。
“券”小于半圆
“撞”空而不实
实际问题
抽象问题
建系
实际运用
P95-1.赵州桥的跨度是37.4m,圆拱高约为7.2m,求这座圆拱桥的拱圆方程。
实际问题
抽象问题
代数问题
析:圆心C在y轴上
建系
C
O
x
y
实际运用
P95-1.赵州桥的跨度是37.4m,圆拱高约为7.2m,求这座圆拱桥的拱圆方程。
实际问题
抽象问题
代数问题
建系
C
O
思考:现有一辆观光船,宽12m,水面以上高5m,这艘船能否从桥下通过?
x
y
实际运用
P94-例4.一个小岛周围有环岛暗礁,暗礁分布在以小岛中心为圆心,半径为20km的圆形区域内,已知小岛中心位于轮船正西40km处,港口位于小岛中心正北30km处,如果轮船沿直线返岗,那么它是否会有触礁危险?
O
x
y
解:以小岛中心为原点O,东西方向为x轴,建立如图的平面直角坐标系,取10km为单位长度,
则港口所在点为B(0,3),轮船所在点为A(4,0),
则环岛暗礁所在圆形区域的边缘所在圆的方程为x2+y2=4,
∴轮船沿直线返岗不会有触礁危险.
THANKS
2.5.2 圆与圆的位置关系
选择性必修第一册 第二章《直线和圆的方程》
问题1:在平面中,圆与圆的位置关系有几种?
问题2:类比直线与圆位置关系的判定方法,如何判断圆与圆的位置关系?
两圆的交点个数
圆心距与两半径的关系
两圆方程的公共解个数
外离
相交
内含
外切
内切
新知1:圆与圆位置关系的判定
圆与圆的位置关系 外离 外切 相交 内切 内含
图示
两圆交点个数 0个 1个 2个 1个 0个
几何法:圆心距d与R±r的关系
代数法:联立两圆方程,消元所得方程解的个数(△的正负)
当Δ=0或Δ<0时,不能确定两圆的位置关系
巩固:圆与圆位置关系的判定
外切或内切
巩固:圆与圆位置关系的判定
建
设
限
代
化
新知2:两圆的公共弦
1.公共弦的定义:两圆相交时两个交点的连线;
2.公共弦的性质:相交两圆的连心线垂直平分其公共弦。
练习2.已知两圆相交于两点A(1,3)和B(m,-1),且两圆圆心都在直线x-y+c=0上,,则m+c的值为 .
新知2:两圆的公共弦
3.求两圆公共弦所在直线方程:
法2:两圆方程作差
法1:联立两圆方程求交点,由两点求直线方程
新知2:两圆的公共弦
3.求两圆公共弦所在直线方程:
法2:两圆方程作差
[注]①当两圆方程中二次项系数相同时,才能作差求解,否则应先化同系数.
②两圆相切时,(*)表示过切点且垂直于连心线的切线方程;
③两圆外离或内含时,(*)表示垂直于连心线的直线方程;
法1:联立两圆方程求交点,由两点求直线方程
4.求两圆公共弦长:
法1:联立两圆方程求交点,求两点距离
法2:求公共弦所在直线方程+垂径定理
典例详解:圆与圆位置关系的判定及公共弦问题
典例详解:圆与圆位置关系的判定及公共弦问题
相交
综合巩固——公共弦问题
【结论】若圆的一条直径的端点分别是A(x ,y ),B(x ,y ),则此圆的方程是(x-x )(x-x )+(y-y1)(y-y )=0.
解:(2)直线PA,PB是圆Q的切线.
因为点A,B在圆 上,且PQ是直径,
所以PA⊥AQ,PB⊥BQ ,所以直线PA,PB是圆Q的切线.
(3)将两圆方程 ,
相减,得6x+5y-25=0,即直线AB的方程是6x+5y-25=0.
小结:两圆的公共弦问题
1.公共弦的性质:相交两圆的连心线垂直平分其公共弦。
2.求两圆公共弦所在直线方程:两圆方程作差
①两圆相切时,(*)表示过切点且垂直于连心线的切线方程;
②两圆外离或内含时,(*)表示垂直于连心线的直线方程;
3.求两圆公共弦长:
求公共弦所在直线方程+垂径定理
综合巩固——公共弦问题
练习2.两圆x2+y2+2ax+2ay+2a2-3=0与x2+y2+2bx+2by+2b2-1=0
公共弦长的最大值为( C ) A.0 B.1 C.2 D.3
综合巩固——公共弦问题
练习3.(多选)已知圆C1:x2+y2=r2,圆C2:(x-a)2+(y-b)2=r2(r>0)
交于不同的A(x1,y1),B(x2,y2)两点,下列结论正确的有( ABC )
A.a(x1-x2)+b(y1-y2)=0 B.2ax1+2by1=a2+b2
C.x1+x2=a D.y1+y2=2b
要点速览
圆系方程的结论及运用
两圆的公切线问题
圆上的点到定直线的距离为定值的点的个数
回顾:直线系方程
当λ(λ∈R)变化时,方程A1x+B1y+C1+λ(A2x+B2y+C2)=0表示过直线
l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0交点的直线束方程,但不包括直线l2.
(不包括直线2x-y+3=0)
(不包括直线x+3y-1=0)
问题:类比上述直线系方程的形式和推导过程,尝试写出过两圆交点的圆系方程.
新知3:圆系方程
当λ(λ∈R)变化时,方程A1x+B1y+C1+λ(A2x+B2y+C2)=0表示过直线
l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0交点的直线束方程,但不包括直线l2.
巩固应用:圆系方程
求圆心
求半径
巩固应用:圆系方程
P98-8.求圆心在x-y-4=0上,且过圆x2+y2+6x-4=0和圆x2+y2+6y-28=0的交点的圆的方程.
巩固应用:圆系方程
P98-7.求经过点M(2,-2)以及圆x2+y2-6x=0与圆x2+y2=4交点的圆的方程.
[变式]求过直线x+2y-3=0与圆x2+y2-2x=0的交点,且圆心在y轴上的圆方程.
巩固应用:圆系方程
P98-8.求圆心在x-y-4=0上,且过圆x2+y2+6x-4=0和圆x2+y2+6y-28=0的交点的圆方程.
新知4:圆的相切问题
和两个圆都相切的直线叫做这两个圆的公切线。
外公切线:两圆在公切线的同旁。
内公切线:两圆在公切线的两侧。
位置关系 图形 公切线条数
外离 4
外切 3
相交 2
内切 1
内含 0
练习1.圆C1:x2+y2-2x-6y+1=0与圆C2:x2+y2+4x+2y+1=0的公切线有(C)
A.1条 B.2条 C.3条 D.4条
练习2.平面直角坐标系中,点A(0,1)和点B(4,5)到直线l的距离分别为1和2,则符合条件的直线l的条数为( 4 )条
巩固运用:圆的相切问题
圆上的点到到定直线的距离为定值的点的个数
d=r+1:1个
0≤d
d=r-1:3个
圆上的点到直线距离为a(a
直线与圆的方程的应用
选择性必修第一册 第二章《直线和圆的方程》
实际运用
P93-例3.如图是某圆拱桥的一孔圆拱的示意图。该圆拱跨度AB=20m,拱高OP=4m,在建造时每隔4m需要用一个支柱支撑,求支柱A2P2的长度.
把点P2(–2, y)代入圆的方程,得y=3.86(负值舍去)
解:如图建立平面直角坐标系,圆心在y轴上。设圆心的坐标是C(0,b),圆的半径是r,
则圆的方程为x2+(y–b)2=r2
∴支柱A2P2的长度为3.86米.
用坐标法解决问题的“三步曲”
1、建立适当的平面直角坐标系,用坐标和方程表示问题中的几何元素(如:点、直线、圆),将平面几何问题转化为代数问题.
2、通过代数运算,解决代数问题
3、把代数运算结果“翻译”成几何结论
代数
几何
几何
建系
坐标法
实际运用
P95-1.赵州桥的跨度是37.4m,圆拱高约为7.2m,求这座圆拱桥的拱圆方程。
著名匠师李春设计建造,为石拱桥,又称安济桥,坐落在河北省赵县的洨河上。经过无数次洪水冲击、风吹雨打、冰雪风霜的侵蚀和8次地震的考验,却安然无恙。
“券”小于半圆
“撞”空而不实
实际问题
抽象问题
建系
实际运用
P95-1.赵州桥的跨度是37.4m,圆拱高约为7.2m,求这座圆拱桥的拱圆方程。
实际问题
抽象问题
代数问题
析:圆心C在y轴上
建系
C
O
x
y
实际运用
P95-1.赵州桥的跨度是37.4m,圆拱高约为7.2m,求这座圆拱桥的拱圆方程。
实际问题
抽象问题
代数问题
建系
C
O
思考:现有一辆观光船,宽12m,水面以上高5m,这艘船能否从桥下通过?
x
y
实际运用
P94-例4.一个小岛周围有环岛暗礁,暗礁分布在以小岛中心为圆心,半径为20km的圆形区域内,已知小岛中心位于轮船正西40km处,港口位于小岛中心正北30km处,如果轮船沿直线返岗,那么它是否会有触礁危险?
O
x
y
解:以小岛中心为原点O,东西方向为x轴,建立如图的平面直角坐标系,取10km为单位长度,
则港口所在点为B(0,3),轮船所在点为A(4,0),
则环岛暗礁所在圆形区域的边缘所在圆的方程为x2+y2=4,
∴轮船沿直线返岗不会有触礁危险.
THANKS
