2.1 圆 课件(共54张PPT) 2023-2024学年苏科数学九年级上册
文档属性
| 名称 | 2.1 圆 课件(共54张PPT) 2023-2024学年苏科数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-01 09:00:07 | ||
图片预览








文档简介
(共54张PPT)
2.1 圆
战国时期数学家墨子撰写的《墨经》一书中,就有“圆,一中同长也”的记载,你理解这句话的意思吗
圆
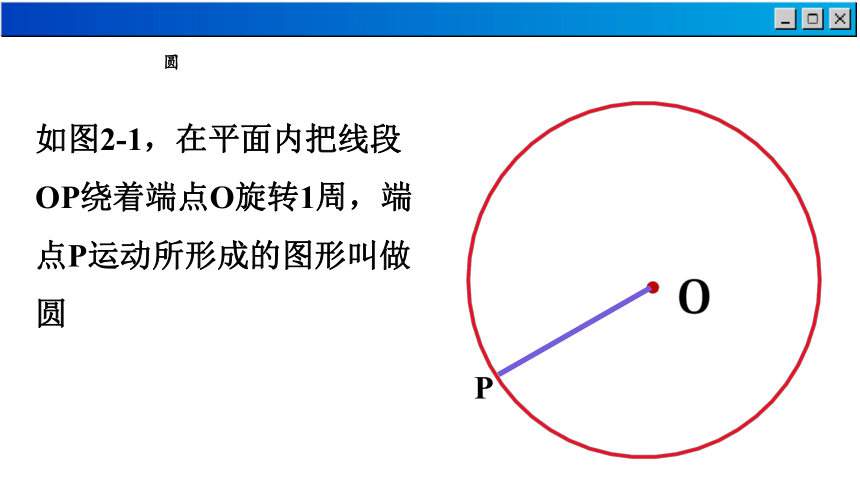
如图2-1,在平面内把线段OP绕着端点O旋转1周,端点P运动所形成的图形叫做圆
P
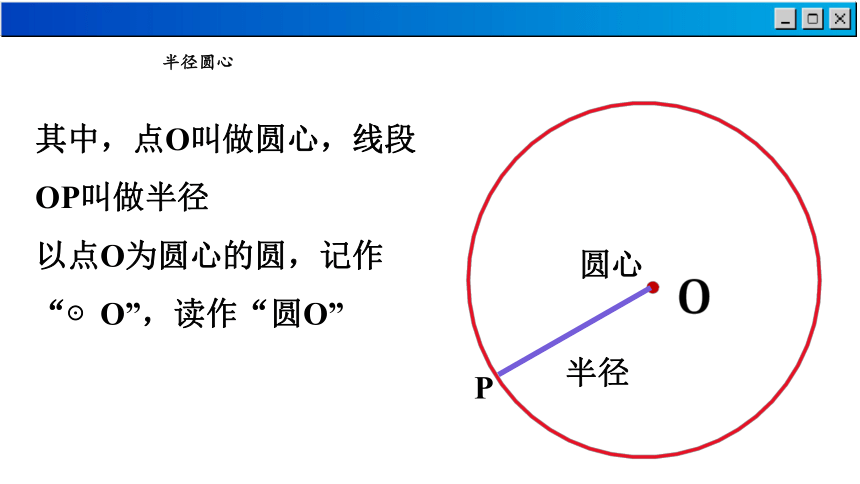
半径圆心
其中,点O叫做圆心,线段OP叫做半径
以点O为圆心的圆,记作“⊙O”,读作“圆O”
圆心
P
半径
操作与思考
在纸上画一个圆、一个点,这个点与圆的位置关系有哪几种 这个点到圆心的距离与圆的半径的大小关系有哪几种 怎样用数量之间思考的关系来描述点与圆的位置关系
操作与思考
在纸上画一个圆、一个点,这个点与圆的位置关系有三种:
①点在圆内 ②点在圆上 ③点在圆外
操作与思考
通过操作、观察可以发现:圆上的点(如图2-2中的点P)到圆心的距离都等于半径,到圆心的距离等于半径的点都在圆上,圆是到定点(圆心)的距离等于定长(半径)的点的集合.
等价于
如果⊙O的半径为r,点P到圆心O的距离为d,
那么点P在圆内d点P在圆上d=r
点P在圆外d>r
符号“”读作“等价于”,它表示从左端可以推出右端,从右端也可以推出左端。
尝试与交流
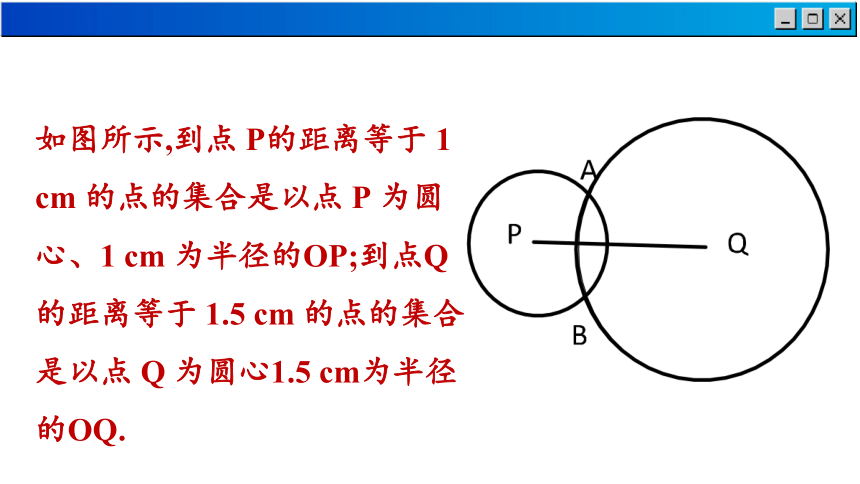
如图2-3,线段PQ=2cm.
(1)画出下列图形:到点P的距离等于1cm的点的集合;到点Q的距离等于1.5cm的点的集合
如图所示,到点 P的距离等于 1 cm 的点的集合是以点 P 为圆心、1 cm 为半径的OP;到点Q的距离等于 1.5 cm 的点的集合是以点 Q 为圆心1.5 cm为半径的OQ.
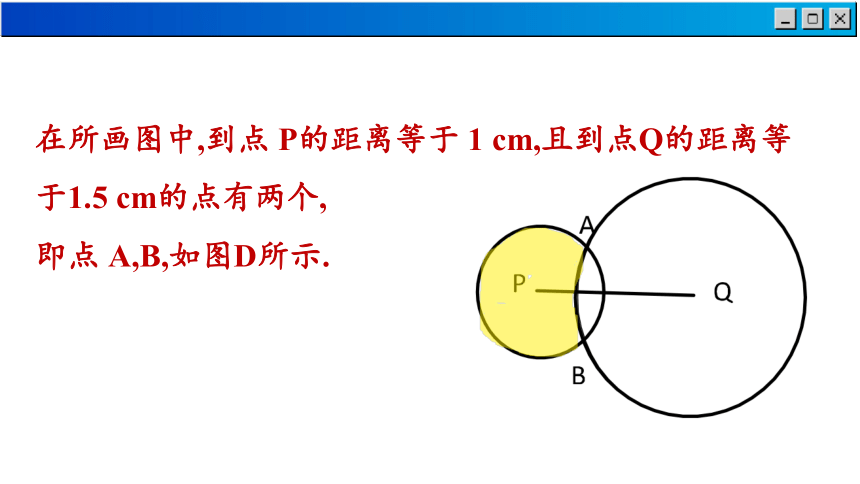
(2)在所画图中,到点P的距离等于1cm,且到点Q的距离等于1.5cm的点有几个 在图中将它们表示出来
在所画图中,到点 P的距离等于 1 cm,且到点Q的距离等于1.5 cm的点有两个,
即点 A,B,如图D所示.
(3)在所画图中,到点P的距离小于或等于1cm,且到点Q的距离大于或等于15cm的点的集合是怎样的图形 在图中将它表示出来
在所画图中,到点 P的距离小于或等于 1cm且到点Q的距离大于或等于 1.5 cm 的点的集合是如图②中阴影部分(包括阴影部分的边界)所示的图形.
练习
1.已知OO的半径为4cm.如果点P到圆心O的距离为4.5cm,那么点P与OO有怎样的位置关系 如果点P到圆心O的距离分别为4cm、3cm 呢
解:点P到圆心O的距离为4.5 cm时,点 P在⊙O外,点P到圆心O的距离为4 cm 时,点P在OO#点P到圆心O的距离为3cm时,点P在⊙O内
练习
2.用图形表示到点A的距离小于或等于2cm的点的集合
到点 A 的距离小于或等于 2 cm 的点的集合就点A 为圆心,2 cm 为半径的圆及圆的内部,如图所示
到点 A 的距离小于或等于 2 cm 的点
的集合就点A 为圆心,2 cm
为半径的圆及圆的内部,如图所示
练习
3.已知矩形ABCD的对角线AC、BD相交于点0,点A、BC、D是否在以点0为圆心的同一个圆上 为什么
解:点A,B,C,D 在以点0为圆心的同一个圆上
∵四边形ABCD 为矩形,
∴OA=OB=OC=OD,
∴根据圆的定义可知,4,B,C,D 在以点O为圆心的同一个圆上
弦
连接圆上任意两点的线段叫做弦。经过圆心的弦叫做直径,CD是⊙O的弦,”
圆弧
AB是⊙ O的直径圆上任意两点间的部分叫做圆弧,简称弧,用符号“⌒”表示。如图2-4,以为端点的弧,记作 ,读作“弧CD
⌒
劣弧 优弧
圆的任意一条直径的两个端点把圆分成两条弧,每条弧都叫做半圆大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧,如图,BAC是优弧,BC是劣弧
优弧
劣弧
圆心角
顶点在圆心的角叫做圆心角。如图2-6,∠AOB是圆心角。
同心圆等弧
圆心相同,半径不相等的两个圆叫做同心圆。能够互相重合的两个圆叫做等圆。能够互相重合的弧叫做等弧
同圆或等圆的半径相等
例题
如图2-7,点A、B和点C、D分别在以点为圆心的两个同心圆上,且∠AOB= ∠ COD。 ∠ C与∠ D相等吗 为什么
解答
解:∠C与∠ D相等
∵ ∠ AOB = ∠ COD
∴ ∠ BOC = ∠ AOD. ∵OB=0A,OC=OD(同圆的半径相等)
∴△BOC≌△AOD
∴ ∠ C= ∠ D.
思考与探索 (教材第41页)
如图2-8,AB是⊙ 的直径,C是BA延长线上一点,点D在⊙ O上,且CD=OA,CD的延长线交⊙ O于点E.若∠C=20°,求∠ BOE 的度数
思考与探索 (教材第41页)
如图所示,连接 OD.
∵CD=0A,OA=OD ∴CD=OD
∵∠C=20°∴∠COD=20°
∴∠0DE=∠C+∠COD=40°
∵OD=OE ∴∠OED=∠ODE=40°
∴∠BOE=∠C+∠OED=20°+40°=60°
练习
1.如图,点A、B、C、D在⊙ O上,在图中画出以这4点中的2点为端点的弦,这样的弦共有几条 是哪几条
这样的弦共 6 条
练习
2.在图中,画出⊙ O的两条直径,依次连接这两条直径的端点,得到一个四边形,判断这个四边形的形状,并说明理由.
解:如图所示,AC,BD 为QO 的两条直径,依次连接这两条直径的端点,得到的四边形 ABCD 为矩形理由如下:在四边形 ABCD 中,由线段 AC,BD 相交,且 OA=OB=0C=OD,得四边形ABCD 是矩形
练习
3.如图,AB是⊙ O的弦,点C、D在AB上,且AC=BD.判断△OCD的形状,并说明理由.
解:△OCD 是等腰三角形.理由如下:在⊙0中,
∵OA,OB 是半径
∴OA=OB,∠0AB=∠OBA.
又AC=BD,
∴△OAC≌△OBD(SAS)
∴OC=OD,.
∴△OCD 是等腰三角形
习题2.1
1.已知⊙ O的半径为3cm,A是线段OP的中点,根据下列条件判断点A与⊙ O的位置关系:
①OP=4cm
当OP=4 cm时,OA=OP=2 cm.
∵2<3,∴点A 在⊙O内.
②OP=6cm
当OP=6 cm时,OA=OP=3 cm.
∵3=3
∴点A在⊙0上
③OP=8cm.
当OP=8 cm时,OA=OP=4 cm.
∵4>3
∴点A在⊙O 外.
2.如图,在Rt△ABC中,∠C=90,AC=4,BC=3。E、F分别是AB、AC的中点。以点B为圆心,BC为半径画圆,判断点A、C、E、F与⊙ B的位置关系,并说明理由。
解:点A 在OB外,点C在⊙B 上,点E在⊙B 内,点F在⊙B 外.理由如下:
连接 BF(图略).在 RtA△ABC 中,
AB=
⊙B 的半径BC=3.
∵BA>BC ∴点A 在⊙B 外,
∵BC=BC ∴点C在⊙B 上,
∵BE=AB=2.5,BE在 Rt△BFC 中,BF=
∵BF>BC ∴点F在⊙B 外.
3.在矩形ABCD中,AB=5,AD=12,以点A为圆心画圆,使点B在OA内,点C在OA外,求OA的半径r的取值范围.
解:∵AB=5 ∴要使点 B 在⊙A 内,则r>5.
连接AC(图略).在 Rt△ADC 中,
AC=
∴要使点C在⊙A外,则r<13 ∴54.如图,BD、CE是△ABC的高,M是BC的中点,点B、C、D、E是否在以点M为圆心的同一个圆上 为什么
解:点 B,C,D,E 在以点M 为圆心的同一个圆上连接 MD,ME(图略).
∵M是BC的中点 ∴MB=MC=BC
在 Rt△BEC 中,EM=BC.
同理,可得 DM=BC.
∵MB-MC=ME-MD=BC,
∴根据圆的定义可知,点 B,C,D,E 在以点M 为圆心的同一个圆上.
5.如图,AB是⊙ O的直径,点C在⊙ O上,且CD⊥AB,垂足为D,CD=4.OD=3.求AB的长。
解:如图,连接 OC,在 Rt△ODC 中,CD=4,OD=3,∠ODC=90°,
∴OC==
∴AB=2OC=2×5=10.
6。如图,OA、OB是OO的半径,C、D分别是OA、OB的中点AD与BC相等吗 为什么
解:AD=BC.如图,∵C是OA 的中点,D是OB 的中点,
∴OC=OA,OD=OB.
又OA,OB 为⊙O的半径,
∴0A=OB,∴OD=OC.
又∠O=∠0,OA=OB
∴△AOD≌△BOC,∴AD=BC.
7.如图,在以点O为圆心的两个同心圆中,大圆的半径OA、OB分别交小圆于点C、D.AB与CD 有怎样的位置关系 为什么
解:AB//CD.
∵OA=OB,OC=OD,
∴∠B=∠A,∠ODC=∠OCD.
在△AOB 中,∠A+∠B=180°-∠O,
在△COD 中,∠0CD+∠ODC=180°-∠O
∴∠A+∠B=∠OCD+∠ODC
∴2∠A=2∠OCD,即∠A=∠OCD,
∴AB//CD.
8.如图, ⊙ O的直径AB=4,半径OC⊥AB,点D在BC上,DE ⊥ OC,DF ⊥ AB,垂足分别为E、F。求EP的长
解:如图,连接 OD.
∵OC⊥OB,DE⊥OC
∴∠COB=90°,∠DEO=90°
又DF⊥AB ∴∠DFO=90°
∴四边形EDFO是矩形,
∴OD=EF=AB.
∵AB=4,
∴EF=2,即 EF 的长是 2.
2.1 圆
战国时期数学家墨子撰写的《墨经》一书中,就有“圆,一中同长也”的记载,你理解这句话的意思吗
圆
如图2-1,在平面内把线段OP绕着端点O旋转1周,端点P运动所形成的图形叫做圆
P
半径圆心
其中,点O叫做圆心,线段OP叫做半径
以点O为圆心的圆,记作“⊙O”,读作“圆O”
圆心
P
半径
操作与思考
在纸上画一个圆、一个点,这个点与圆的位置关系有哪几种 这个点到圆心的距离与圆的半径的大小关系有哪几种 怎样用数量之间思考的关系来描述点与圆的位置关系
操作与思考
在纸上画一个圆、一个点,这个点与圆的位置关系有三种:
①点在圆内 ②点在圆上 ③点在圆外
操作与思考
通过操作、观察可以发现:圆上的点(如图2-2中的点P)到圆心的距离都等于半径,到圆心的距离等于半径的点都在圆上,圆是到定点(圆心)的距离等于定长(半径)的点的集合.
等价于
如果⊙O的半径为r,点P到圆心O的距离为d,
那么点P在圆内d
点P在圆外d>r
符号“”读作“等价于”,它表示从左端可以推出右端,从右端也可以推出左端。
尝试与交流
如图2-3,线段PQ=2cm.
(1)画出下列图形:到点P的距离等于1cm的点的集合;到点Q的距离等于1.5cm的点的集合
如图所示,到点 P的距离等于 1 cm 的点的集合是以点 P 为圆心、1 cm 为半径的OP;到点Q的距离等于 1.5 cm 的点的集合是以点 Q 为圆心1.5 cm为半径的OQ.
(2)在所画图中,到点P的距离等于1cm,且到点Q的距离等于1.5cm的点有几个 在图中将它们表示出来
在所画图中,到点 P的距离等于 1 cm,且到点Q的距离等于1.5 cm的点有两个,
即点 A,B,如图D所示.
(3)在所画图中,到点P的距离小于或等于1cm,且到点Q的距离大于或等于15cm的点的集合是怎样的图形 在图中将它表示出来
在所画图中,到点 P的距离小于或等于 1cm且到点Q的距离大于或等于 1.5 cm 的点的集合是如图②中阴影部分(包括阴影部分的边界)所示的图形.
练习
1.已知OO的半径为4cm.如果点P到圆心O的距离为4.5cm,那么点P与OO有怎样的位置关系 如果点P到圆心O的距离分别为4cm、3cm 呢
解:点P到圆心O的距离为4.5 cm时,点 P在⊙O外,点P到圆心O的距离为4 cm 时,点P在OO#点P到圆心O的距离为3cm时,点P在⊙O内
练习
2.用图形表示到点A的距离小于或等于2cm的点的集合
到点 A 的距离小于或等于 2 cm 的点的集合就点A 为圆心,2 cm 为半径的圆及圆的内部,如图所示
到点 A 的距离小于或等于 2 cm 的点
的集合就点A 为圆心,2 cm
为半径的圆及圆的内部,如图所示
练习
3.已知矩形ABCD的对角线AC、BD相交于点0,点A、BC、D是否在以点0为圆心的同一个圆上 为什么
解:点A,B,C,D 在以点0为圆心的同一个圆上
∵四边形ABCD 为矩形,
∴OA=OB=OC=OD,
∴根据圆的定义可知,4,B,C,D 在以点O为圆心的同一个圆上
弦
连接圆上任意两点的线段叫做弦。经过圆心的弦叫做直径,CD是⊙O的弦,”
圆弧
AB是⊙ O的直径圆上任意两点间的部分叫做圆弧,简称弧,用符号“⌒”表示。如图2-4,以为端点的弧,记作 ,读作“弧CD
⌒
劣弧 优弧
圆的任意一条直径的两个端点把圆分成两条弧,每条弧都叫做半圆大于半圆的弧叫做优弧,小于半圆的弧叫做劣弧,如图,BAC是优弧,BC是劣弧
优弧
劣弧
圆心角
顶点在圆心的角叫做圆心角。如图2-6,∠AOB是圆心角。
同心圆等弧
圆心相同,半径不相等的两个圆叫做同心圆。能够互相重合的两个圆叫做等圆。能够互相重合的弧叫做等弧
同圆或等圆的半径相等
例题
如图2-7,点A、B和点C、D分别在以点为圆心的两个同心圆上,且∠AOB= ∠ COD。 ∠ C与∠ D相等吗 为什么
解答
解:∠C与∠ D相等
∵ ∠ AOB = ∠ COD
∴ ∠ BOC = ∠ AOD. ∵OB=0A,OC=OD(同圆的半径相等)
∴△BOC≌△AOD
∴ ∠ C= ∠ D.
思考与探索 (教材第41页)
如图2-8,AB是⊙ 的直径,C是BA延长线上一点,点D在⊙ O上,且CD=OA,CD的延长线交⊙ O于点E.若∠C=20°,求∠ BOE 的度数
思考与探索 (教材第41页)
如图所示,连接 OD.
∵CD=0A,OA=OD ∴CD=OD
∵∠C=20°∴∠COD=20°
∴∠0DE=∠C+∠COD=40°
∵OD=OE ∴∠OED=∠ODE=40°
∴∠BOE=∠C+∠OED=20°+40°=60°
练习
1.如图,点A、B、C、D在⊙ O上,在图中画出以这4点中的2点为端点的弦,这样的弦共有几条 是哪几条
这样的弦共 6 条
练习
2.在图中,画出⊙ O的两条直径,依次连接这两条直径的端点,得到一个四边形,判断这个四边形的形状,并说明理由.
解:如图所示,AC,BD 为QO 的两条直径,依次连接这两条直径的端点,得到的四边形 ABCD 为矩形理由如下:在四边形 ABCD 中,由线段 AC,BD 相交,且 OA=OB=0C=OD,得四边形ABCD 是矩形
练习
3.如图,AB是⊙ O的弦,点C、D在AB上,且AC=BD.判断△OCD的形状,并说明理由.
解:△OCD 是等腰三角形.理由如下:在⊙0中,
∵OA,OB 是半径
∴OA=OB,∠0AB=∠OBA.
又AC=BD,
∴△OAC≌△OBD(SAS)
∴OC=OD,.
∴△OCD 是等腰三角形
习题2.1
1.已知⊙ O的半径为3cm,A是线段OP的中点,根据下列条件判断点A与⊙ O的位置关系:
①OP=4cm
当OP=4 cm时,OA=OP=2 cm.
∵2<3,∴点A 在⊙O内.
②OP=6cm
当OP=6 cm时,OA=OP=3 cm.
∵3=3
∴点A在⊙0上
③OP=8cm.
当OP=8 cm时,OA=OP=4 cm.
∵4>3
∴点A在⊙O 外.
2.如图,在Rt△ABC中,∠C=90,AC=4,BC=3。E、F分别是AB、AC的中点。以点B为圆心,BC为半径画圆,判断点A、C、E、F与⊙ B的位置关系,并说明理由。
解:点A 在OB外,点C在⊙B 上,点E在⊙B 内,点F在⊙B 外.理由如下:
连接 BF(图略).在 RtA△ABC 中,
AB=
⊙B 的半径BC=3.
∵BA>BC ∴点A 在⊙B 外,
∵BC=BC ∴点C在⊙B 上,
∵BE=AB=2.5,BE
∵BF>BC ∴点F在⊙B 外.
3.在矩形ABCD中,AB=5,AD=12,以点A为圆心画圆,使点B在OA内,点C在OA外,求OA的半径r的取值范围.
解:∵AB=5 ∴要使点 B 在⊙A 内,则r>5.
连接AC(图略).在 Rt△ADC 中,
AC=
∴要使点C在⊙A外,则r<13 ∴5
解:点 B,C,D,E 在以点M 为圆心的同一个圆上连接 MD,ME(图略).
∵M是BC的中点 ∴MB=MC=BC
在 Rt△BEC 中,EM=BC.
同理,可得 DM=BC.
∵MB-MC=ME-MD=BC,
∴根据圆的定义可知,点 B,C,D,E 在以点M 为圆心的同一个圆上.
5.如图,AB是⊙ O的直径,点C在⊙ O上,且CD⊥AB,垂足为D,CD=4.OD=3.求AB的长。
解:如图,连接 OC,在 Rt△ODC 中,CD=4,OD=3,∠ODC=90°,
∴OC==
∴AB=2OC=2×5=10.
6。如图,OA、OB是OO的半径,C、D分别是OA、OB的中点AD与BC相等吗 为什么
解:AD=BC.如图,∵C是OA 的中点,D是OB 的中点,
∴OC=OA,OD=OB.
又OA,OB 为⊙O的半径,
∴0A=OB,∴OD=OC.
又∠O=∠0,OA=OB
∴△AOD≌△BOC,∴AD=BC.
7.如图,在以点O为圆心的两个同心圆中,大圆的半径OA、OB分别交小圆于点C、D.AB与CD 有怎样的位置关系 为什么
解:AB//CD.
∵OA=OB,OC=OD,
∴∠B=∠A,∠ODC=∠OCD.
在△AOB 中,∠A+∠B=180°-∠O,
在△COD 中,∠0CD+∠ODC=180°-∠O
∴∠A+∠B=∠OCD+∠ODC
∴2∠A=2∠OCD,即∠A=∠OCD,
∴AB//CD.
8.如图, ⊙ O的直径AB=4,半径OC⊥AB,点D在BC上,DE ⊥ OC,DF ⊥ AB,垂足分别为E、F。求EP的长
解:如图,连接 OD.
∵OC⊥OB,DE⊥OC
∴∠COB=90°,∠DEO=90°
又DF⊥AB ∴∠DFO=90°
∴四边形EDFO是矩形,
∴OD=EF=AB.
∵AB=4,
∴EF=2,即 EF 的长是 2.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
