2.5 直线与圆的位置关系 课件(共98张PPT) 2023-2024学年苏科数学九年级上册
文档属性
| 名称 | 2.5 直线与圆的位置关系 课件(共98张PPT) 2023-2024学年苏科数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-01 09:04:15 | ||
图片预览



文档简介
(共98张PPT)
直线与圆的位置关系
新课导入
山水相接的地方出现了一道红霞。过了一会儿,那里出现了太阳的小半边脸,慢慢儿,一纵一纵地使劲儿向上升。到了最后它终于冲破了云霞,完全跳出了海面,
操作与思考
在纸上画一个圆,上、下移动直尺,如果将直尺的边缘看作一条直线,那么在移动直尺的过程中,直线与圆的位置关系发生了怎样的变化
这种位置的变化可以用数量之间的关系来描述吗
答案
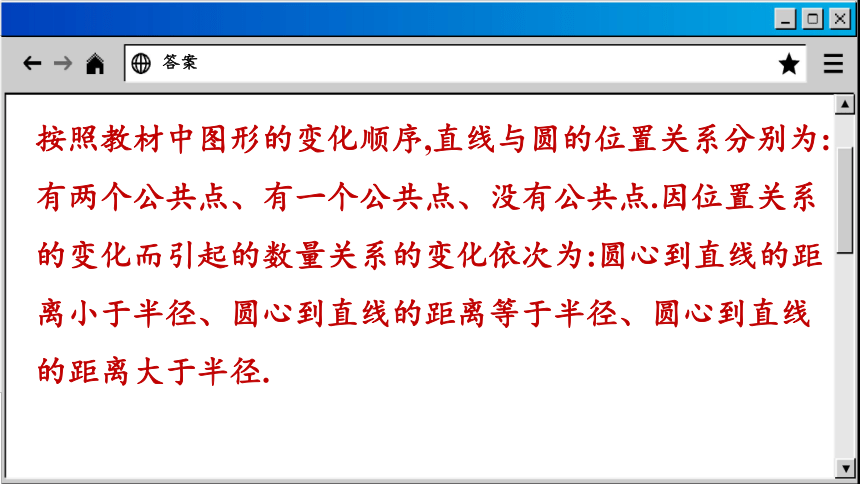
按照教材中图形的变化顺序,直线与圆的位置关系分别为:有两个公共点、有一个公共点、没有公共点.因位置关系的变化而引起的数量关系的变化依次为:圆心到直线的距离小于半径、圆心到直线的距离等于半径、圆心到直线的距离大于半径.
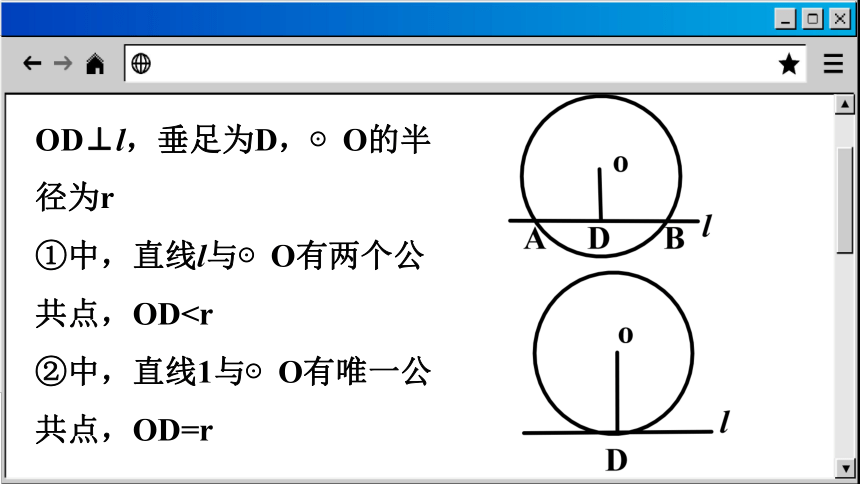
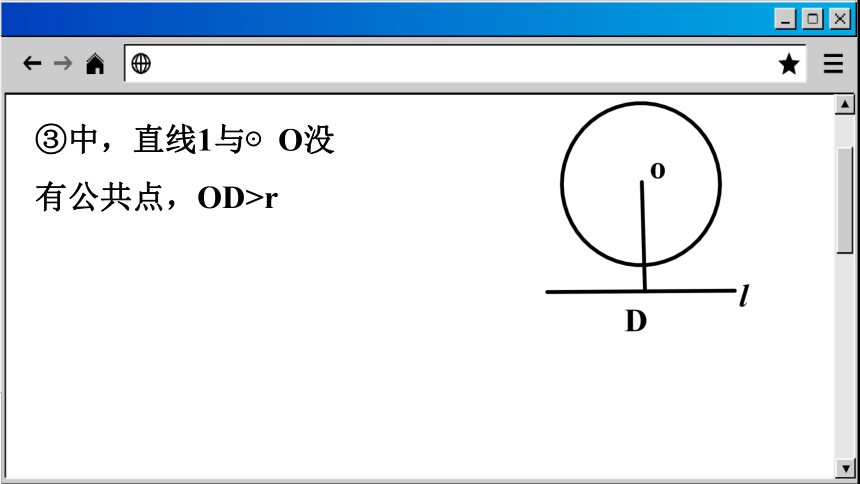
OD⊥l,垂足为D,⊙O的半径为r
①中,直线l与⊙O有两个公共点,OD②中,直线1与⊙O有唯一公共点,OD=r
③中,直线1与⊙O没有公共点,OD>r
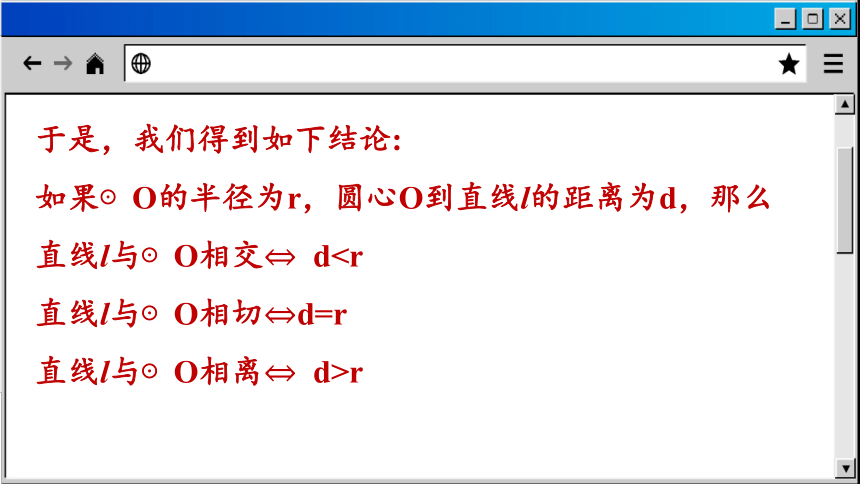
于是,我们得到如下结论:
如果⊙O的半径为r,圆心O到直线l的距离为d,那么
直线l与⊙O相交d直线l与⊙O相切d=r
直线l与⊙O相离d>r
思考与探索(教材第 64 页)
点与圆有3种不同的位置关系,直线与圆也有3种不同的位置关系,这两者之间有怎样的联系
从图2-37中可以看出,直线l与⊙O的3种位置关系,实质上就是点D《垂足》与⊙O的3种位置关系
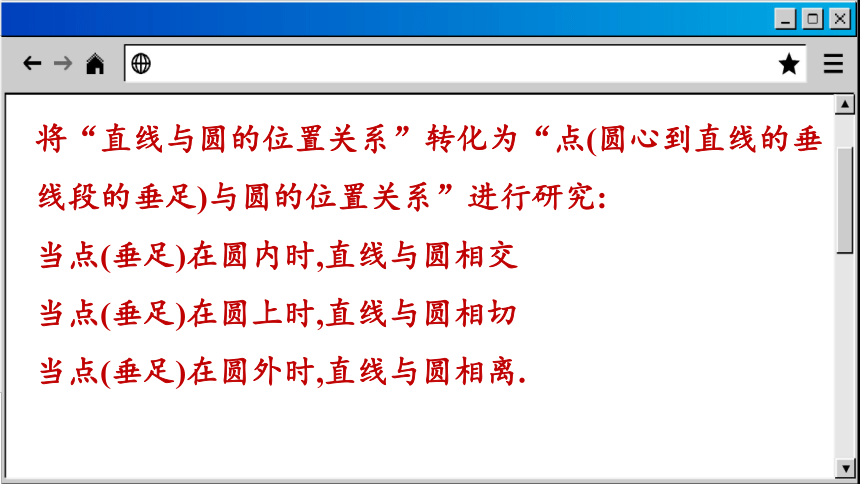
将“直线与圆的位置关系”转化为“点(圆心到直线的垂线段的垂足)与圆的位置关系”进行研究:
当点(垂足)在圆内时,直线与圆相交
当点(垂足)在圆上时,直线与圆相切
当点(垂足)在圆外时,直线与圆相离.
例1
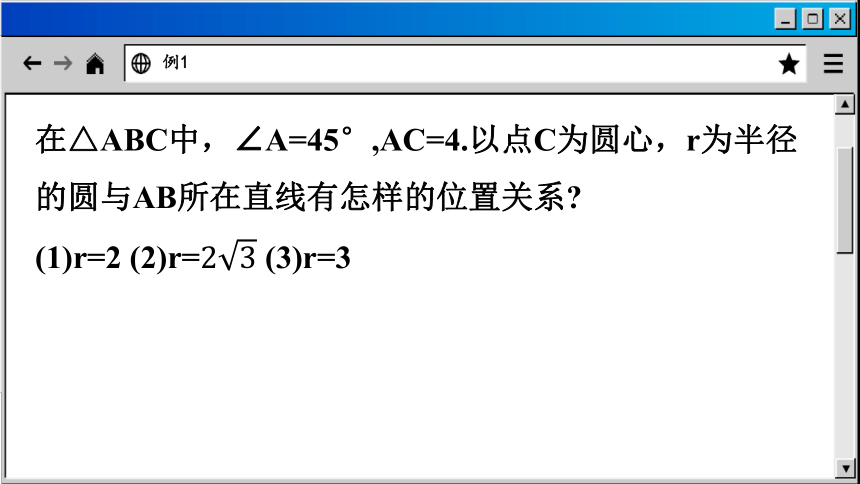
在△ABC中,∠A=45°,AC=4.以点C为圆心,r为半径的圆与AB所在直线有怎样的位置关系
(1)r=2 (2)r= (3)r=3
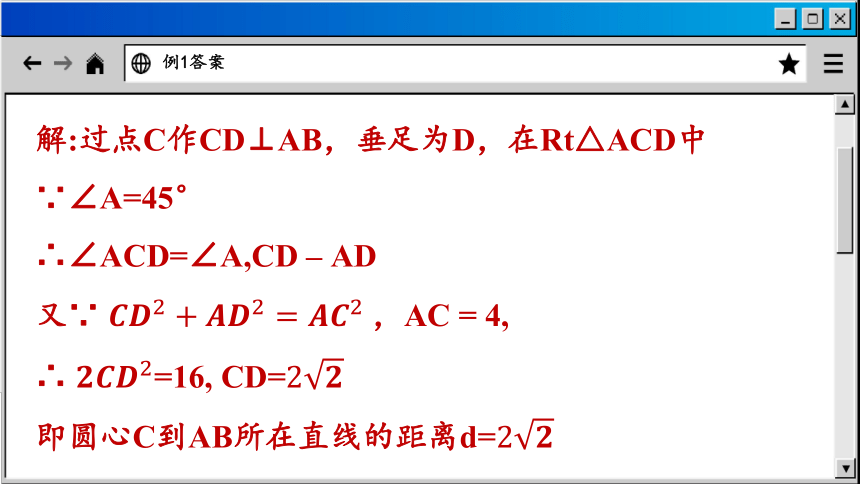
例1答案
解:过点C作CD⊥AB,垂足为D,在Rt△ACD中
∵∠A=45°
∴∠ACD=∠A,CD – AD
又∵ ,AC = 4,
∴ =16, CD=
即圆心C到AB所在直线的距离d=
相离
(1)当r-2时,d>r,⊙C与AB所在直线相离
相切
(2)当r=2V2时d=r ⊙C与AB所在直线相切
相交
(3)当r-3时,d1.填表
直线与圆的位置关系 图形 公共点个数 直线的名称 公共点名称 圆心到直线的距离d与半径r的关系
相交
相切
相离
2.已知⊙O的直径为8,圆心⊙O到直线1的距离为5,直线l与⊙O有怎样的位置关系 圆心O到直线l的距离为4或3呢
操作与思考
在图2-39中,经过⊙O的半径OD的外端点D,作直线l ⊥OD直线l与⊙O有怎样的位置关系 为什么
直线l与⊙O相切
于是,我们得到如下结论:经过半径的外端并且垂直于这条半径的直线是圆的切线
思考与探索
如图2-41,直线1是⊙O的切线,切点为D,直线l与半径OD有怎样的位置关系 为什么
直线l与⊙O垂直
我们可以用反证法证明l⊥OD
假设直线l与OD不垂直,过圆心O作OD'⊥l,垂足为D'(如图2-42)
因为直线l与⊙O相切,所以圆心O到直线的l距离OD'等于⊙O的半径,点D'在⊙O上.这样,直线l与⊙O有两个公共点D、D'.这与“直线l与⊙O相切”矛盾,所以l⊥OD。
于是,我们得到如下结论:
圆的切线垂直于经过切点的半径
例题2
如图2-43,△ABC是⊙O的内接三角形,AB是⊙O的直径,∠CAD=∠ABC。判断直线AD与⊙O的位置关系,并说明理由。
解:直线AD与⊙O相切,
∵AB是OO的直径,
∴∠ACB =90°
∴∠ABC+∠BAC =90°
又∵∠CAD= ∠ABC,
∴∠CAD+∠BAC=90°
即 AD⊥AB.
∴直线AD与⊙O相切(经过半径的外端并且垂直于这条半径的直线是圆的切线).
例题3
如图2-44,AB是⊙O的直径,弦AD平分∠BAC,过点D的切线交AC 于点E。DE与AC有怎样的位置关系 为什么
解:DE与AC互相垂直.连接OD.
∵OD =OA,
∴∠ODA = ∠OAD.
又∵∠0AD= ∠CAD,
∴∠ODA = ∠CAD.
∴OD ∥ AC.
∵DE是⊙O的切线
∴DE⊥OD(圆的切线垂直于经过切点的半径),即∠ODE=90°.于是,∠DEA=90°,DE⊥AC.
1.如图,点P在⊙O上,过点P西⊙O的切线
2.如图,AB是⊙O的直径,∠ABC=45°,AB=AC,直线AC与⊙O有怎样的位置关系 为什么
*3,如图,在以点O为圆心的两个同心圈中,大圈的弦AB切小圆于点P。PA与PB相等吗 为什么
尝试与交流
要从一块三角形铁皮余料中剪一个圆,如何使剪得的圆面积最大
观察图2-45 可以发现,要使剪得的圆面积最大,这个圆应与三角形的各边都相切。
思考与探索
如何作一个圆,使它与已知三角形的各边都相切
圆心到三角形的三边的距离相等.
圆心在三角形的内角平分线上.
已知△ABC。根据下列作法,用直尺和圆规作⊙ O,使它与△ ABC的各边都相切?
作 法 图形
1.分别作∠ABC、∠ACB 的平分线 BM、CN,BM与CN 的交点为0. 2.过点O,作OD⊥BC,垂足为 D 3.以点O为圆心,OD 为半径作⊙O. ⊙O就是所求作的圆.
与三角形各边都相切的圆叫做三角形的内切圆.内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形,如图2-46,⊙O是△ABC的内切圆,△ABC是⊙O的外切三角形
例4
如图2-47,⊙O是△ABC的内切圆,切点分别为 D、E、F,∠B=60°,∠C=70,求∠EDF的度数.
解:连接OE、OF.
在△ABC中,
∠A=180°-(∠B+∠C)
∠A=180°-(∠B+∠C)
=180°-(60°+70)
=50°
∵⊙O是△ABC的内切圆,
∴AB⊥OF,AC⊥OE
(圈的切线垂直于经过切点的半径).
1.如图,点O是△ABC的内心,根据下列条件,求∠BOC的度数.
(1)∠ABC =50° ∠ACB=60°
(2)∠A=50°
2.如图,点C、D分别在射线OA、OB上,求作OP,使它与OA、OB、CD都相切.
①分别作∠AOB,∠DCO 的平分线,两平分线交于点 P1
②过点 P1,作 PE⊥OA,垂足为 E.
③以点 P1,为圆心,PE 为半径作OP1
④同理,得到⊙P2
⊙P1,⊙P2就是所求作的圆,如图所示.
尝试与交流
如图2-48,PA、PB是OO的切线,切点分别为A、BPA与PB相等吗
度量可知PA=PB
图2-48是轴对称图形,
PA与PB相等
我们可以用下面的方法证实小明、小丽的猜想:
在图2-48中,连接OA、OB、OP(如图2-49),
∵PA、PB是⊙O的切线,
∴PA⊥OA,PB⊥OB
(圈的切线垂直于
经过切点的半径).
即△POA、△POB 是直角三角形
又∵OA=OB.OP=OP
∴△POA≌△POB.
∴ PA=PB.
我们也可以运用图形运动的方法证实 PA=PB.
在图2-49中,由OA⊥PA,
OB⊥PB.OA=OB,可知点O在∠APB的平分线上
于是,把图2-49中的PB沿直线OP翻折,射线PB与射线PA重合(如图2-50)
因为过点O有且只有一条直线与PA(PB)垂直,所以OB与OA 重合即点 B与点A重合,PA=PB.
在经过圆外一点的圆的切线上,这点与切点之间的线段的长,叫做这点到圆的切线长。
于是,我们得到如下定理:
过圆外一点所画的圆的两条切线长相等
例5
如图2-51,在以点0为圆心的两个同心圆中,大圆的弦 AB、AC分别与小圆相切于点D、E。AB与AC相等吗 为什么
解:AB与AC相等
连接OD、OE。
∵AB、AC是小圆的两条切线,切点分别为 D、E
∴AD=AE(过图外一点所画的图的两条切线长相等)
∴AB⊥OD,ACB⊥OE(圆的切线垂直于经过切点的半径)又∵AB、AC是大圆的弦,OD⊥AB,OE⊥AC.
∴AB=2AD,AC=2AE.
∴AB =AC.
拓展与延伸(教材第 72 页)
在图2-51中,如果连接 DE、BC,那么DE与BC 有怎样的关系 为什么
*1,如图,AB、AC、BD是⊙O的切线,切点分别为P、C、D.若AB=5,AC=3,求 BD的长.
*2.如图,PA、PB是⊙O的切线,切点分别为A、B,直线OP交⊙O于点C、D,交AB 于点E,根据题设条件,你能得到哪些结论 为什么
习题 2.5
1.已知⊙O的直径为10,圆心O到直线l的距离为3,直线l与⊙O有怎样的位置关系 圆心O到直线l的距离为5或8呢
∵⊙O的直径为 10,
∴⊙O的半径为 5.
当圆心 O 到直线l的距离为 3 时,直线l与O相交
当圆心 O 到直线l的距离为 5 时,直线l与O相切;
当圆心 O 到直线l的距离为 8 时,直线l与O相离。
2.如图, ⊙O的半径为,AB、AC是⊙O的两条弦,AB ,AC=4,如果以点O为圆心作一个与AC 相切的圆,那么这个图的半径是多少 它与AB 所在直线有怎样的位置关系
3.如图,在Rt是△ABC中,∠C=90°.AC=3.BC=4.以点C为圆心,r为半径的圆与AB 所在直线有怎样的位置关系
(1)r=2:(2)r=2.4;(3)r=3.
(1)当r=2时,因为d>r,所以圆与 AB 所在的直线相离
(2)当r=2.4 时,因为 d=r,所以圆与 AB 所在的直线相切
(3)当r=3时,因为 d4.如图,AB是⊙O的直径,AD是⊙O的弦,过点B的切线交AD的延长线于点C,若AD=DC,∠ABD的度数
解:∵AB 是⊙O 的直径
∴∠BDA=∠BDC=90°
又∵AD=DC,BD=BD,
∴△ABD≌△CBD(SAS).
∴∠ABD=∠CBD.
又∵CB 为⊙O的切线
∴∠ABC=90°.
∠ABD=×90°=45°
5.如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠D=30°,求∠ A的度数。
解:如图,连接 OC.
∵CD 是⊙O 的切线,点 C 为切点
∴OC⊥CD,
又∵∠D=30°
∴∠COD=60°=∠A+∠ACO,
又∵OA=OC
∴∠A=∠ACO,
∴∠A=∠COD=×60°=30°
6.如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,直线AB与⊙O相切吗 为什么
解:AB 与⊙O 相切
如图,连接 OC.
∵OA=OB,CA=CB,OC=OC
∴△AOC≌△BOC ∴∠OCA=∠OCB.
又∵∠0CA+∠OCB=180°
∴∠OCA=∠OCB=90°,即OC⊥AB
∴直线 AB 与⊙O相切
7.如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,判断△CBP的形状,并说明理由.
解:△CBP 是等腰三角形.理由如下
∵BC切⊙O 于点B ∴OB⊥CB.
∴∠CBP+∠OBA=90°
∵OC⊥OA ∴∠OPA+∠OAP=90°.
∵OA=OB ∴∠OAP=∠OBA
∴∠OPA=∠CBP..
∵∠OPA=∠CPB∴∠CBP=∠CPB。.
∴△CBP 是等腰三角形.
8.如图,P是∠BAC的平分线上一点,PD⊥AC,垂足为 D.AB与以点P为圈心,PD为半径的圈相切吗 为什么
解:相切.
如图,过点P作PE⊥AB,垂足为 E.
∵AP 是∠BAC 的平分线,PD⊥AC,..
∴PE=PD.
又∵PD 为半径 ∴PE 也为半径.
∴AB 与以点 P为圆心,PD 为半径的圆相切
9,如图,已知Rt△ABC(∠C=90°),作一个圈,使圆心O在AC上,且与AB、BC所在直线相切(不写作法,保留作图痕迹,并说明作图的理由)
解:如图所示,⊙O就是所求作的圆.
作图理由如下:由所作的⊙O与AB,BC 所在的直线相切可知,圆心O到AB,BC 的距离相等,由此想到“到角两边距离相等的点在角的平分线上”,因此作∠ABC 的平分线.
因为圆心 O在AC 上,所以所求作的圆的圆心O为∠ABC 的平分线与AC 的交点以点O 为圆心,OC 为半径(OC⊥BC)所作的⊙O即为所求作的圆.
10.如图,I是△ABC的内心,AI的延长线交△ABC的外接圆于点D,BD与ID相等吗 为什么
解:BD=ID.
如图所示,连接 BI.
∵I 是△ABC 的内心
∴BI 平分∠ABC,AD 平分∠BAC
∴∠IBC=∠IBA,∠BAD=∠CAD=∠CBD.
∵∠IBC+∠CBD=∠IBD,∠IBA+∠BAD=∠DIB
∴∠IBD=∠DIB
∴BD=ID.
11.如图,△ABC的周长为 24,面积为48,求它的内切圆的半径。
解:如图,设O为△ABC 的内心,内切圆的半径为r,三个切点分别为 D,E,F,连接 OD,OE,OF,0A,OB,OC,
∴OD⊥AB,OE⊥AC,OF⊥BC,OD=OE=OF
∴S△ABC = S△AOB 十S△BOC 十S△AOC
AB·OD+BC·OF+AC·OE
=r(AB+BC+AC).
∵S△ABC =24,AB+BC+AC=24,
∴r24=24,解得r=2.
∴△ABC 的内切圆的半径为 2.
*12.如图,PA、PB是⊙O的切线,切点分别为A、B,点C在弧AB上,过点C的切线分别交PA、PB于点D、E。设PA=10,求△PDE的周长。
解:∵DA,DC与⊙O 相切
∴DA=DC.
同理可得 EC=EB,PA=PB.
∵PA=10,
∴△PDE 的周长为 PD+DE +PE
=PD+DC+CE+PE
=PD+DA+EB+PE
=PA+PB
=2PA=20.
*13.如图,四边形ABCD的各边与⊙O分别相切于点E、F、G、H。AB、BC、CD、DA之间有怎样的数量关系 为什么
解:AB+CD=DA+BC
∵AE,AH 是⊙O的切线
∴AE=AH
同理可得 BE=BF,CF=CG,DG=DH.
∴AB +CD =AE +BE +DG +CG
=AH +BF+DH+CF
=DA+BC
即AB+CD=DA+BC.
*14.如图,AB是⊙O的切线,切点为 BAO交⊙O于点C,过点C的切线交AB 于点D,若AD=2BD,CD=2.求⊙O的半径
解:连接 OB(图略).
∵DC切O0 于点C ∴DC⊥OA.
又∵DB切⊙O于点B,
∴DC=DB=2∴AD=2BD=4.
∴AB=BD+AD=6.
在Rt△DCA 中,AC===2,
设⊙O的半径为 r.
在 Rt△ABO 中,+=
即 =,解得r=2
∴⊙O的半径为 2
阅读
圆与圆的位置关系
借助学习点与圈、直线与圈的位置关系所获得的经验,我们未探索圆与圆的位置关系.在平面内,两圆相对运动,可以得到下列不同的位置关系(如图(1)):
这5种位置关系分别称为两圈外离、外切、相交、内切和内含.像点与图、直线与圆的位置关系那样,圈与图的位置关系与相应的数量关系之间也有着内在的联系。如围(2),设⊙ O1、 ⊙ O2 :的半径分别为 R、r,圆心0、O:之间的距离为d.
观察图(2),我们可以用d与R、r之间的数量关系来描述两圆的位置关系:
两圆外离d>R+r;
两圆外切d=R+r;
两圆相交R-rr)
两圆内切d=R-r(R> r)
两圆内含dr)
图形的位置关系决定了相应数量之间的关系,反过来,由数量之间的关系可以判定图形的位置关系。
直线与圆的位置关系
新课导入
山水相接的地方出现了一道红霞。过了一会儿,那里出现了太阳的小半边脸,慢慢儿,一纵一纵地使劲儿向上升。到了最后它终于冲破了云霞,完全跳出了海面,
操作与思考
在纸上画一个圆,上、下移动直尺,如果将直尺的边缘看作一条直线,那么在移动直尺的过程中,直线与圆的位置关系发生了怎样的变化
这种位置的变化可以用数量之间的关系来描述吗
答案
按照教材中图形的变化顺序,直线与圆的位置关系分别为:有两个公共点、有一个公共点、没有公共点.因位置关系的变化而引起的数量关系的变化依次为:圆心到直线的距离小于半径、圆心到直线的距离等于半径、圆心到直线的距离大于半径.
OD⊥l,垂足为D,⊙O的半径为r
①中,直线l与⊙O有两个公共点,OD
③中,直线1与⊙O没有公共点,OD>r
于是,我们得到如下结论:
如果⊙O的半径为r,圆心O到直线l的距离为d,那么
直线l与⊙O相交d
直线l与⊙O相离d>r
思考与探索(教材第 64 页)
点与圆有3种不同的位置关系,直线与圆也有3种不同的位置关系,这两者之间有怎样的联系
从图2-37中可以看出,直线l与⊙O的3种位置关系,实质上就是点D《垂足》与⊙O的3种位置关系
将“直线与圆的位置关系”转化为“点(圆心到直线的垂线段的垂足)与圆的位置关系”进行研究:
当点(垂足)在圆内时,直线与圆相交
当点(垂足)在圆上时,直线与圆相切
当点(垂足)在圆外时,直线与圆相离.
例1
在△ABC中,∠A=45°,AC=4.以点C为圆心,r为半径的圆与AB所在直线有怎样的位置关系
(1)r=2 (2)r= (3)r=3
例1答案
解:过点C作CD⊥AB,垂足为D,在Rt△ACD中
∵∠A=45°
∴∠ACD=∠A,CD – AD
又∵ ,AC = 4,
∴ =16, CD=
即圆心C到AB所在直线的距离d=
相离
(1)当r-2时,d>r,⊙C与AB所在直线相离
相切
(2)当r=2V2时d=r ⊙C与AB所在直线相切
相交
(3)当r-3时,d
直线与圆的位置关系 图形 公共点个数 直线的名称 公共点名称 圆心到直线的距离d与半径r的关系
相交
相切
相离
2.已知⊙O的直径为8,圆心⊙O到直线1的距离为5,直线l与⊙O有怎样的位置关系 圆心O到直线l的距离为4或3呢
操作与思考
在图2-39中,经过⊙O的半径OD的外端点D,作直线l ⊥OD直线l与⊙O有怎样的位置关系 为什么
直线l与⊙O相切
于是,我们得到如下结论:经过半径的外端并且垂直于这条半径的直线是圆的切线
思考与探索
如图2-41,直线1是⊙O的切线,切点为D,直线l与半径OD有怎样的位置关系 为什么
直线l与⊙O垂直
我们可以用反证法证明l⊥OD
假设直线l与OD不垂直,过圆心O作OD'⊥l,垂足为D'(如图2-42)
因为直线l与⊙O相切,所以圆心O到直线的l距离OD'等于⊙O的半径,点D'在⊙O上.这样,直线l与⊙O有两个公共点D、D'.这与“直线l与⊙O相切”矛盾,所以l⊥OD。
于是,我们得到如下结论:
圆的切线垂直于经过切点的半径
例题2
如图2-43,△ABC是⊙O的内接三角形,AB是⊙O的直径,∠CAD=∠ABC。判断直线AD与⊙O的位置关系,并说明理由。
解:直线AD与⊙O相切,
∵AB是OO的直径,
∴∠ACB =90°
∴∠ABC+∠BAC =90°
又∵∠CAD= ∠ABC,
∴∠CAD+∠BAC=90°
即 AD⊥AB.
∴直线AD与⊙O相切(经过半径的外端并且垂直于这条半径的直线是圆的切线).
例题3
如图2-44,AB是⊙O的直径,弦AD平分∠BAC,过点D的切线交AC 于点E。DE与AC有怎样的位置关系 为什么
解:DE与AC互相垂直.连接OD.
∵OD =OA,
∴∠ODA = ∠OAD.
又∵∠0AD= ∠CAD,
∴∠ODA = ∠CAD.
∴OD ∥ AC.
∵DE是⊙O的切线
∴DE⊥OD(圆的切线垂直于经过切点的半径),即∠ODE=90°.于是,∠DEA=90°,DE⊥AC.
1.如图,点P在⊙O上,过点P西⊙O的切线
2.如图,AB是⊙O的直径,∠ABC=45°,AB=AC,直线AC与⊙O有怎样的位置关系 为什么
*3,如图,在以点O为圆心的两个同心圈中,大圈的弦AB切小圆于点P。PA与PB相等吗 为什么
尝试与交流
要从一块三角形铁皮余料中剪一个圆,如何使剪得的圆面积最大
观察图2-45 可以发现,要使剪得的圆面积最大,这个圆应与三角形的各边都相切。
思考与探索
如何作一个圆,使它与已知三角形的各边都相切
圆心到三角形的三边的距离相等.
圆心在三角形的内角平分线上.
已知△ABC。根据下列作法,用直尺和圆规作⊙ O,使它与△ ABC的各边都相切?
作 法 图形
1.分别作∠ABC、∠ACB 的平分线 BM、CN,BM与CN 的交点为0. 2.过点O,作OD⊥BC,垂足为 D 3.以点O为圆心,OD 为半径作⊙O. ⊙O就是所求作的圆.
与三角形各边都相切的圆叫做三角形的内切圆.内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形,如图2-46,⊙O是△ABC的内切圆,△ABC是⊙O的外切三角形
例4
如图2-47,⊙O是△ABC的内切圆,切点分别为 D、E、F,∠B=60°,∠C=70,求∠EDF的度数.
解:连接OE、OF.
在△ABC中,
∠A=180°-(∠B+∠C)
∠A=180°-(∠B+∠C)
=180°-(60°+70)
=50°
∵⊙O是△ABC的内切圆,
∴AB⊥OF,AC⊥OE
(圈的切线垂直于经过切点的半径).
1.如图,点O是△ABC的内心,根据下列条件,求∠BOC的度数.
(1)∠ABC =50° ∠ACB=60°
(2)∠A=50°
2.如图,点C、D分别在射线OA、OB上,求作OP,使它与OA、OB、CD都相切.
①分别作∠AOB,∠DCO 的平分线,两平分线交于点 P1
②过点 P1,作 PE⊥OA,垂足为 E.
③以点 P1,为圆心,PE 为半径作OP1
④同理,得到⊙P2
⊙P1,⊙P2就是所求作的圆,如图所示.
尝试与交流
如图2-48,PA、PB是OO的切线,切点分别为A、BPA与PB相等吗
度量可知PA=PB
图2-48是轴对称图形,
PA与PB相等
我们可以用下面的方法证实小明、小丽的猜想:
在图2-48中,连接OA、OB、OP(如图2-49),
∵PA、PB是⊙O的切线,
∴PA⊥OA,PB⊥OB
(圈的切线垂直于
经过切点的半径).
即△POA、△POB 是直角三角形
又∵OA=OB.OP=OP
∴△POA≌△POB.
∴ PA=PB.
我们也可以运用图形运动的方法证实 PA=PB.
在图2-49中,由OA⊥PA,
OB⊥PB.OA=OB,可知点O在∠APB的平分线上
于是,把图2-49中的PB沿直线OP翻折,射线PB与射线PA重合(如图2-50)
因为过点O有且只有一条直线与PA(PB)垂直,所以OB与OA 重合即点 B与点A重合,PA=PB.
在经过圆外一点的圆的切线上,这点与切点之间的线段的长,叫做这点到圆的切线长。
于是,我们得到如下定理:
过圆外一点所画的圆的两条切线长相等
例5
如图2-51,在以点0为圆心的两个同心圆中,大圆的弦 AB、AC分别与小圆相切于点D、E。AB与AC相等吗 为什么
解:AB与AC相等
连接OD、OE。
∵AB、AC是小圆的两条切线,切点分别为 D、E
∴AD=AE(过图外一点所画的图的两条切线长相等)
∴AB⊥OD,ACB⊥OE(圆的切线垂直于经过切点的半径)又∵AB、AC是大圆的弦,OD⊥AB,OE⊥AC.
∴AB=2AD,AC=2AE.
∴AB =AC.
拓展与延伸(教材第 72 页)
在图2-51中,如果连接 DE、BC,那么DE与BC 有怎样的关系 为什么
*1,如图,AB、AC、BD是⊙O的切线,切点分别为P、C、D.若AB=5,AC=3,求 BD的长.
*2.如图,PA、PB是⊙O的切线,切点分别为A、B,直线OP交⊙O于点C、D,交AB 于点E,根据题设条件,你能得到哪些结论 为什么
习题 2.5
1.已知⊙O的直径为10,圆心O到直线l的距离为3,直线l与⊙O有怎样的位置关系 圆心O到直线l的距离为5或8呢
∵⊙O的直径为 10,
∴⊙O的半径为 5.
当圆心 O 到直线l的距离为 3 时,直线l与O相交
当圆心 O 到直线l的距离为 5 时,直线l与O相切;
当圆心 O 到直线l的距离为 8 时,直线l与O相离。
2.如图, ⊙O的半径为,AB、AC是⊙O的两条弦,AB ,AC=4,如果以点O为圆心作一个与AC 相切的圆,那么这个图的半径是多少 它与AB 所在直线有怎样的位置关系
3.如图,在Rt是△ABC中,∠C=90°.AC=3.BC=4.以点C为圆心,r为半径的圆与AB 所在直线有怎样的位置关系
(1)r=2:(2)r=2.4;(3)r=3.
(1)当r=2时,因为d>r,所以圆与 AB 所在的直线相离
(2)当r=2.4 时,因为 d=r,所以圆与 AB 所在的直线相切
(3)当r=3时,因为 d
解:∵AB 是⊙O 的直径
∴∠BDA=∠BDC=90°
又∵AD=DC,BD=BD,
∴△ABD≌△CBD(SAS).
∴∠ABD=∠CBD.
又∵CB 为⊙O的切线
∴∠ABC=90°.
∠ABD=×90°=45°
5.如图,AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若∠D=30°,求∠ A的度数。
解:如图,连接 OC.
∵CD 是⊙O 的切线,点 C 为切点
∴OC⊥CD,
又∵∠D=30°
∴∠COD=60°=∠A+∠ACO,
又∵OA=OC
∴∠A=∠ACO,
∴∠A=∠COD=×60°=30°
6.如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,直线AB与⊙O相切吗 为什么
解:AB 与⊙O 相切
如图,连接 OC.
∵OA=OB,CA=CB,OC=OC
∴△AOC≌△BOC ∴∠OCA=∠OCB.
又∵∠0CA+∠OCB=180°
∴∠OCA=∠OCB=90°,即OC⊥AB
∴直线 AB 与⊙O相切
7.如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,判断△CBP的形状,并说明理由.
解:△CBP 是等腰三角形.理由如下
∵BC切⊙O 于点B ∴OB⊥CB.
∴∠CBP+∠OBA=90°
∵OC⊥OA ∴∠OPA+∠OAP=90°.
∵OA=OB ∴∠OAP=∠OBA
∴∠OPA=∠CBP..
∵∠OPA=∠CPB∴∠CBP=∠CPB。.
∴△CBP 是等腰三角形.
8.如图,P是∠BAC的平分线上一点,PD⊥AC,垂足为 D.AB与以点P为圈心,PD为半径的圈相切吗 为什么
解:相切.
如图,过点P作PE⊥AB,垂足为 E.
∵AP 是∠BAC 的平分线,PD⊥AC,..
∴PE=PD.
又∵PD 为半径 ∴PE 也为半径.
∴AB 与以点 P为圆心,PD 为半径的圆相切
9,如图,已知Rt△ABC(∠C=90°),作一个圈,使圆心O在AC上,且与AB、BC所在直线相切(不写作法,保留作图痕迹,并说明作图的理由)
解:如图所示,⊙O就是所求作的圆.
作图理由如下:由所作的⊙O与AB,BC 所在的直线相切可知,圆心O到AB,BC 的距离相等,由此想到“到角两边距离相等的点在角的平分线上”,因此作∠ABC 的平分线.
因为圆心 O在AC 上,所以所求作的圆的圆心O为∠ABC 的平分线与AC 的交点以点O 为圆心,OC 为半径(OC⊥BC)所作的⊙O即为所求作的圆.
10.如图,I是△ABC的内心,AI的延长线交△ABC的外接圆于点D,BD与ID相等吗 为什么
解:BD=ID.
如图所示,连接 BI.
∵I 是△ABC 的内心
∴BI 平分∠ABC,AD 平分∠BAC
∴∠IBC=∠IBA,∠BAD=∠CAD=∠CBD.
∵∠IBC+∠CBD=∠IBD,∠IBA+∠BAD=∠DIB
∴∠IBD=∠DIB
∴BD=ID.
11.如图,△ABC的周长为 24,面积为48,求它的内切圆的半径。
解:如图,设O为△ABC 的内心,内切圆的半径为r,三个切点分别为 D,E,F,连接 OD,OE,OF,0A,OB,OC,
∴OD⊥AB,OE⊥AC,OF⊥BC,OD=OE=OF
∴S△ABC = S△AOB 十S△BOC 十S△AOC
AB·OD+BC·OF+AC·OE
=r(AB+BC+AC).
∵S△ABC =24,AB+BC+AC=24,
∴r24=24,解得r=2.
∴△ABC 的内切圆的半径为 2.
*12.如图,PA、PB是⊙O的切线,切点分别为A、B,点C在弧AB上,过点C的切线分别交PA、PB于点D、E。设PA=10,求△PDE的周长。
解:∵DA,DC与⊙O 相切
∴DA=DC.
同理可得 EC=EB,PA=PB.
∵PA=10,
∴△PDE 的周长为 PD+DE +PE
=PD+DC+CE+PE
=PD+DA+EB+PE
=PA+PB
=2PA=20.
*13.如图,四边形ABCD的各边与⊙O分别相切于点E、F、G、H。AB、BC、CD、DA之间有怎样的数量关系 为什么
解:AB+CD=DA+BC
∵AE,AH 是⊙O的切线
∴AE=AH
同理可得 BE=BF,CF=CG,DG=DH.
∴AB +CD =AE +BE +DG +CG
=AH +BF+DH+CF
=DA+BC
即AB+CD=DA+BC.
*14.如图,AB是⊙O的切线,切点为 BAO交⊙O于点C,过点C的切线交AB 于点D,若AD=2BD,CD=2.求⊙O的半径
解:连接 OB(图略).
∵DC切O0 于点C ∴DC⊥OA.
又∵DB切⊙O于点B,
∴DC=DB=2∴AD=2BD=4.
∴AB=BD+AD=6.
在Rt△DCA 中,AC===2,
设⊙O的半径为 r.
在 Rt△ABO 中,+=
即 =,解得r=2
∴⊙O的半径为 2
阅读
圆与圆的位置关系
借助学习点与圈、直线与圈的位置关系所获得的经验,我们未探索圆与圆的位置关系.在平面内,两圆相对运动,可以得到下列不同的位置关系(如图(1)):
这5种位置关系分别称为两圈外离、外切、相交、内切和内含.像点与图、直线与圆的位置关系那样,圈与图的位置关系与相应的数量关系之间也有着内在的联系。如围(2),设⊙ O1、 ⊙ O2 :的半径分别为 R、r,圆心0、O:之间的距离为d.
观察图(2),我们可以用d与R、r之间的数量关系来描述两圆的位置关系:
两圆外离d>R+r;
两圆外切d=R+r;
两圆相交R-r
两圆内切d=R-r(R> r)
两圆内含d
图形的位置关系决定了相应数量之间的关系,反过来,由数量之间的关系可以判定图形的位置关系。
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
