4.3 等可能条件下的概率(二) 课件(共18张PPT) 2023-2024学年苏科数学九年级上册
文档属性
| 名称 | 4.3 等可能条件下的概率(二) 课件(共18张PPT) 2023-2024学年苏科数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 758.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-01 09:15:48 | ||
图片预览




文档简介
(共18张PPT)
4.3 等可能性条件下的概率(二)
1.在具体情境中进一步理解概率的意义,体会概率是
描述随机现象的数学模型.(重点)
2.在具体情境中感受一类事件发生的概率(能转化为
古典概型的几何概型)的大小与面积的大小有关.
(重点、难点)
学习目标
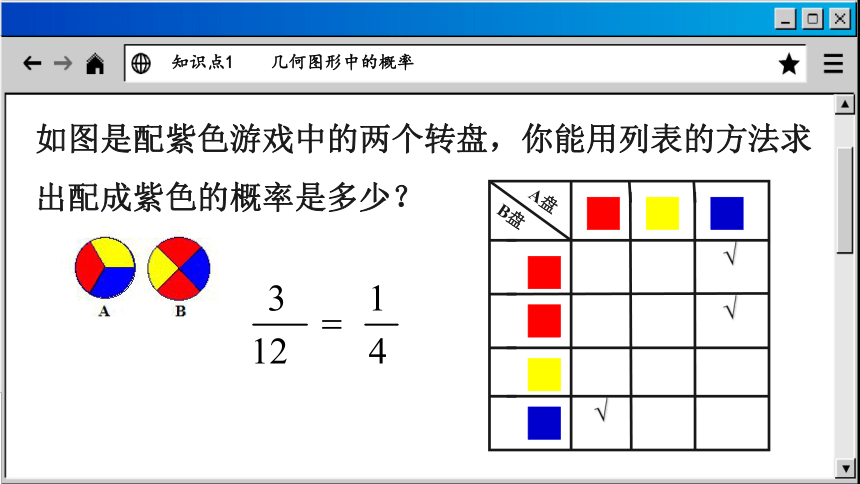
如图是配紫色游戏中的两个转盘,你能用列表的方法求出配成紫色的概率是多少?
新课导入
知识点1 几何图形中的概率
如图是配紫色游戏中的两个转盘,你能用列表的方法求出配成紫色的概率是多少?
√
√
√
B盘
A盘
如图是一个可以自由转动的转盘,转盘分成7个大小相同的扇形,颜色分为红、绿、黄三种颜色.指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形).
红
红
红
绿
绿
黄
黄
知识点1 几何图形中的概率
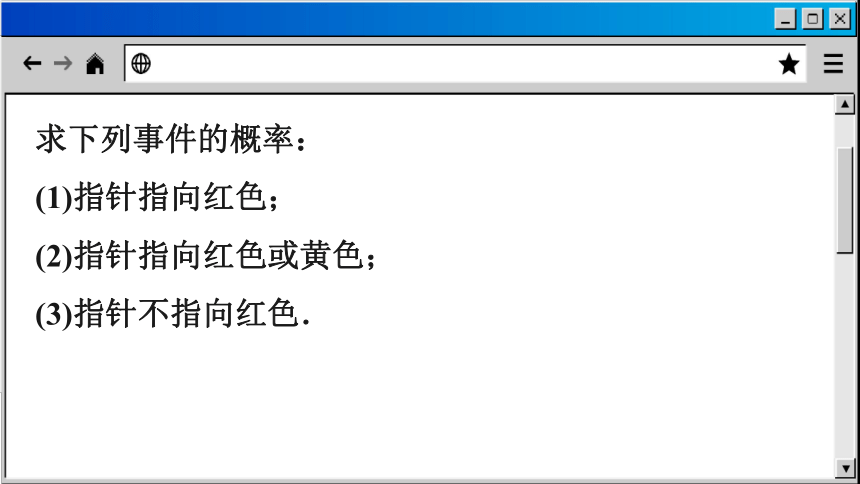
求下列事件的概率:
(1)指针指向红色;
(2)指针指向红色或黄色;
(3)指针不指向红色.
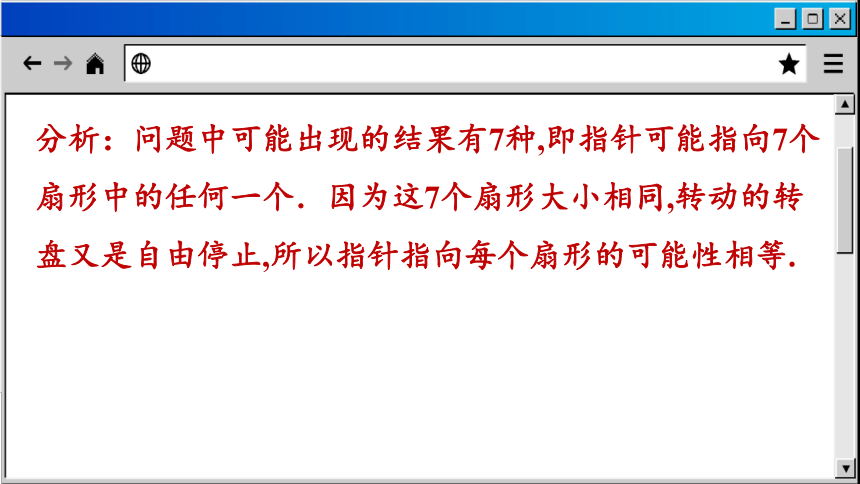
分析:问题中可能出现的结果有7种,即指针可能指向7个扇形中的任何一个.因为这7个扇形大小相同,转动的转盘又是自由停止,所以指针指向每个扇形的可能性相等.
解:按颜色把7个扇形分别记为:红1 ,红2 ,红3 ,绿1 ,
绿2 ,黄1 ,黄2 ,所有可能结果的总数为7,并且它
们出现的可能性相等.
求下列事件的概率:
(1)指针指向红色;
指针指向红色(记为事件A)的结果有3种,即红1 ,
红2 ,红3 ,因此
(2)指针指向红色或黄色
指针指向红色或黄色(记为事件B)的结果有5种,
即红1 ,红2 ,红3 ,黄1 ,黄2 ,因此
(3)指针不指向红色.
指针不指向红色(记为事件C)的结果有4种,即绿1 ,
绿2 ,黄1 ,黄2 ,因此
对于受几何图形的面积影响的随机事件,在一个平面区域内的每个点,事件发生的可能性是相等的,如果所有可能发生的区域面积为S,所求事件A发生的区域面积为S′,则 ,即若将图形等分成若干份,那么事件A发生的概率等于此事件所有可能结果组成的图形所占的份数除以总份数.
在用扇形统计图反映地球上陆地面积与海洋面.积所占的比例时,陆地面积所对应的圆心角是108°.若宇宙中一块陨石落在地球上,则落在陆地上的概率是( ).
A.0.2 B.0.3
C.0.4 D.0.5
B
练一练
几何图形中的概率
课堂小结
用力旋转如图的转盘甲和转盘乙的指针,如果你想让指针停在阴影区域上,那么选择哪个转盘成功的概率大?
当堂小练
解:因为在两个转盘中阴影部分的面积都各自占所在圆面积的,所以成功的概率一样大,都是.
当堂小练
“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.李亮随机地向大正方形内部区域投飞镖,若直角三角形两条直角边的长分别是2和1,则飞镖被投到小正方形(阴影)区域的概率是( )
拓展与延伸
4.3 等可能性条件下的概率(二)
1.在具体情境中进一步理解概率的意义,体会概率是
描述随机现象的数学模型.(重点)
2.在具体情境中感受一类事件发生的概率(能转化为
古典概型的几何概型)的大小与面积的大小有关.
(重点、难点)
学习目标
如图是配紫色游戏中的两个转盘,你能用列表的方法求出配成紫色的概率是多少?
新课导入
知识点1 几何图形中的概率
如图是配紫色游戏中的两个转盘,你能用列表的方法求出配成紫色的概率是多少?
√
√
√
B盘
A盘
如图是一个可以自由转动的转盘,转盘分成7个大小相同的扇形,颜色分为红、绿、黄三种颜色.指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形).
红
红
红
绿
绿
黄
黄
知识点1 几何图形中的概率
求下列事件的概率:
(1)指针指向红色;
(2)指针指向红色或黄色;
(3)指针不指向红色.
分析:问题中可能出现的结果有7种,即指针可能指向7个扇形中的任何一个.因为这7个扇形大小相同,转动的转盘又是自由停止,所以指针指向每个扇形的可能性相等.
解:按颜色把7个扇形分别记为:红1 ,红2 ,红3 ,绿1 ,
绿2 ,黄1 ,黄2 ,所有可能结果的总数为7,并且它
们出现的可能性相等.
求下列事件的概率:
(1)指针指向红色;
指针指向红色(记为事件A)的结果有3种,即红1 ,
红2 ,红3 ,因此
(2)指针指向红色或黄色
指针指向红色或黄色(记为事件B)的结果有5种,
即红1 ,红2 ,红3 ,黄1 ,黄2 ,因此
(3)指针不指向红色.
指针不指向红色(记为事件C)的结果有4种,即绿1 ,
绿2 ,黄1 ,黄2 ,因此
对于受几何图形的面积影响的随机事件,在一个平面区域内的每个点,事件发生的可能性是相等的,如果所有可能发生的区域面积为S,所求事件A发生的区域面积为S′,则 ,即若将图形等分成若干份,那么事件A发生的概率等于此事件所有可能结果组成的图形所占的份数除以总份数.
在用扇形统计图反映地球上陆地面积与海洋面.积所占的比例时,陆地面积所对应的圆心角是108°.若宇宙中一块陨石落在地球上,则落在陆地上的概率是( ).
A.0.2 B.0.3
C.0.4 D.0.5
B
练一练
几何图形中的概率
课堂小结
用力旋转如图的转盘甲和转盘乙的指针,如果你想让指针停在阴影区域上,那么选择哪个转盘成功的概率大?
当堂小练
解:因为在两个转盘中阴影部分的面积都各自占所在圆面积的,所以成功的概率一样大,都是.
当堂小练
“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形.李亮随机地向大正方形内部区域投飞镖,若直角三角形两条直角边的长分别是2和1,则飞镖被投到小正方形(阴影)区域的概率是( )
拓展与延伸
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
