9.2.3总体集中趋势的估计 课件(共28张PPT)
文档属性
| 名称 | 9.2.3总体集中趋势的估计 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-01 19:26:40 | ||
图片预览






文档简介
(共28张PPT)
总体集中趋势的估计
年 级:高 一 学 科:数学(人教A版)
“大数据时代”
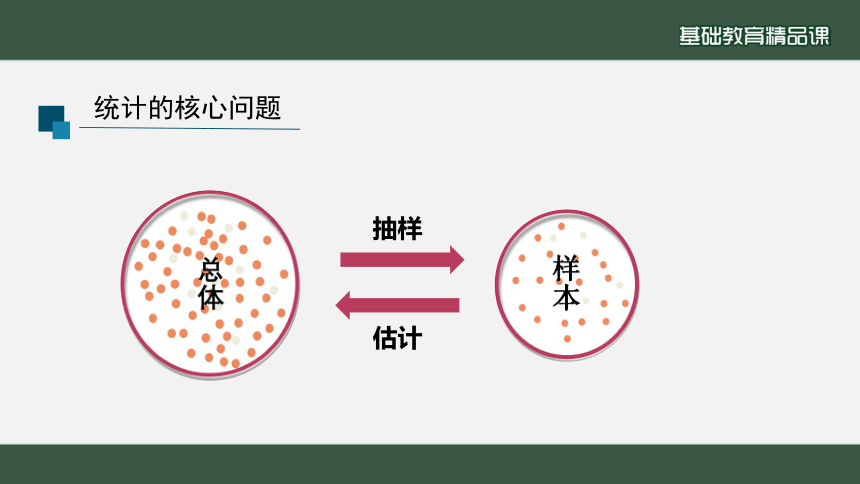
统计的核心问题
抽样
估计
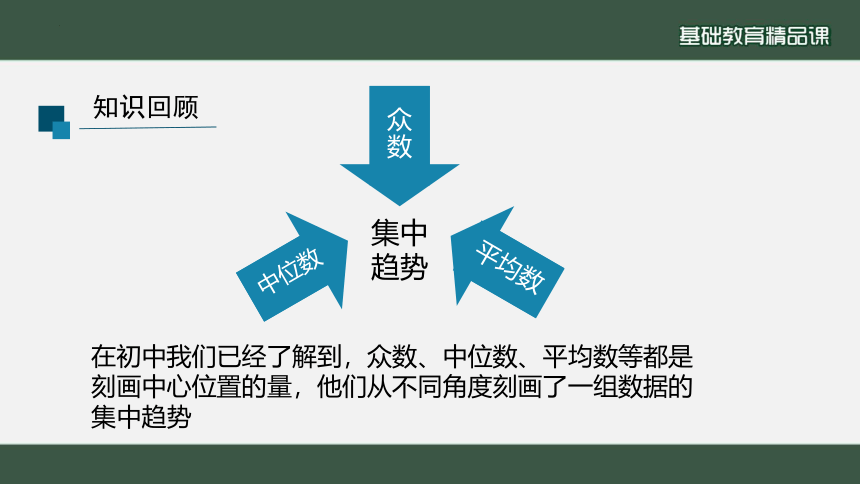
知识回顾
在初中我们已经了解到,众数、中位数、平均数等都是刻画中心位置的量,他们从不同角度刻画了一组数据的集中趋势
集中
趋势
众数
平均数
中位数
Lorem ipsum
众数、中位数、平均数的概念:
一组数据中出现次数最多的数叫做这组数据的众数。
将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数.
中位数
平均数
如果一组数据是 则这组数据的平均数为
众数
探究一:众数、中位数、平均数
9.0 13.6 14.9 5.9 4.0 7.1 6.4 5.4 19.4 2.0 2.2 8.6 13.8 5.4 10.2 4.9 6.8 14.0 2.0 10.5
2.1 5.7 5.1 16.8 6.0 11.1 1.3 11.2 7.7 4.9 2.3 10,0 16.7 12.0 12.4 7.8 5.2 13.6 2.6 22.4
3.6 7.1 8.8 25.6 3.2 18.3 5.1 2.0 3.0 12.0 22.2 10.8 5.5 2.0 24.3 9.9 3.6 5.6 4.4 7.9
5.1 24.5 6.4 7.5 4.7 20.5 5.5 15.7 2.6 5.7 5.5 6.0 16.0 2.4 9.5 3.7 17.0 3.8 4.1 2.3
5.3 7.8 8.1 4.3 13.3 6.8 1.3 7.0 4.9 1.8 7.1 28.0 10.2 13.8 17.9 10.1 5.5 4.6 3.2 21.6
【例】利用9.2.1节中100户居民的月均用水量的调查数据,计算样本数据的众数、平均数和中位数,并据此估计全市居民用户月均用水量的众数、中位数和平均数。
中位数
众数
平均数
众数是2.0和5.5
中位数是
因为数据是抽自全市居民的简单随机样本,所以我们可以据
此估计全市居民用户的月均用水量的众数约为2.0t和5.5t,平均数约为8.79t,其中位数约为6.8t.
探究二:众数、中位数、平均数与频率分布直方图的关系
在某些情况下我们无法获知原始的样本数据。这时该如何估计样本的众数、中位数、平均数?
你能以下面的频率分布直方图提供的信息为例,给出估计方法吗?
一组数据中出现次数最多的数
众数:在样本数据的频率分布直方图中,最高矩形的中点的横坐标。
月均用水量在区间[4.2,7.2)内的居民最多, 可以将这个区间的中点5.7作为众数的估计值.
1.估计众数
频数
频率
将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数.
中位数:把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标。
50%
0.231
0.552
设中位数为 ,
解得
面积
2.估计中位数
3.估计平均数
设 为每一组的频数
中点yi'估计
频率
底边中点横坐标×小矩形面积
n1
y1’
平均数:等于各小矩形的面积乘以其底边中点的横坐标之和。
中点yi'估计
3.估计平均数
由频率分布直方图我们估计出全市居民用户月均用水量的众数是5.7,中位数是6.71,平均数是8.96.
频率分布直方图
众数 5.7
中位数 6.71
平均数 8.96
原始数据
2.0、5.5
6.8
8.79
比较从居民月均用水量样本数据计算出的该样本的众数、中位数、平均数与我们从样本频率分布直方图得出的结论,你发现了什么?
频率分布直方图损失了一些样本数据,得到的是一个估计值,所得估值与数据分组有关.
探究三:众数、中位数、平均数分析
名称 优点 缺点
众数
1. 特征
它只能表达样本数据中很少的一部分信息,无法客观的反映总体的特征.
(1)众数
1.体现样本数据的最大
集中点;
2.容易计算;
3.不受极端值影响.
小明用统计软件计算100户居民用水量的平均数和中位数,但在录入数据时,不小心将一个数据7.7录成了77,请计算录入数据的平均数和中位数,并与真实的样本平均数和中位数作比较,哪个量的值变化更大?你能解释其中的原因吗?
平均数
对极端数据更加敏感
(2)中位数、平均数
名称 优点 缺点
众数
中位数
平均数
1.体现样本数据的最大集中点;
2.容易计算.
它只能表达样本数据中很少的一部分信息,无法客观的反映总体的特征.
1.不受少数几个极端数的影响;
2.容易计算,利用中间数据的信息,反映中等水平.
对极端数据不敏感.
代表性较好,是反映数据集中趋势的量.一般情况下,可以反映更多的根源样本数据全体的信息.
任何一个数据的改变都会引起平均数的改变,数据越“离群”,对平均数的影响越大.
3.不受极端值影响.
例5:某学校要定制高一年级的校服,学生根据厂家提供的参考身高选择校服规格,据统计,高一年级女生需要不同规格校服的频数如表所示。
校服规格 155 160 165 170 175 合计
频数 39 64 167 90 26 386
如果用一个量来代表该校高一年级女生所需校服的规格,那么在中位数、平均数和众数中哪个量比较合适?试讨论用表中的数据估计全国高一年级女生校服规格的合理性。
2. 集中趋势的选择
校服规格 155 160 165 170 175 合计
频数 39 64 167 90 26 386
用众数165作为该校高一年级女生校服的规格比较合适.
由于全国各地的高一年级女生身高存在一定的差异,所以用一个学校的数据估计全国高一年级女生的校服规格不合理.
xs
对分类型数据集中趋势的描述,可以用众数.
校服规格
性别
产品质量等级
如:
视频来源:智联招聘、新浪财经(如图标注)
对数值型数据集中趋势的描述,可以用平均数、中位数.
用水量
身高
产量
如:
收入
所以,我们要强调”用数据说话”,但同时又要防止被误导。
课堂小结
集中
趋势
众数
平均数
中位数
课堂小结
统计的基本思想方法:
抽样收集数据
分析样本数据
对总体进行估计
数据
图表
谢 谢 !
总体集中趋势的估计
年 级:高 一 学 科:数学(人教A版)
“大数据时代”
统计的核心问题
抽样
估计
知识回顾
在初中我们已经了解到,众数、中位数、平均数等都是刻画中心位置的量,他们从不同角度刻画了一组数据的集中趋势
集中
趋势
众数
平均数
中位数
Lorem ipsum
众数、中位数、平均数的概念:
一组数据中出现次数最多的数叫做这组数据的众数。
将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数.
中位数
平均数
如果一组数据是 则这组数据的平均数为
众数
探究一:众数、中位数、平均数
9.0 13.6 14.9 5.9 4.0 7.1 6.4 5.4 19.4 2.0 2.2 8.6 13.8 5.4 10.2 4.9 6.8 14.0 2.0 10.5
2.1 5.7 5.1 16.8 6.0 11.1 1.3 11.2 7.7 4.9 2.3 10,0 16.7 12.0 12.4 7.8 5.2 13.6 2.6 22.4
3.6 7.1 8.8 25.6 3.2 18.3 5.1 2.0 3.0 12.0 22.2 10.8 5.5 2.0 24.3 9.9 3.6 5.6 4.4 7.9
5.1 24.5 6.4 7.5 4.7 20.5 5.5 15.7 2.6 5.7 5.5 6.0 16.0 2.4 9.5 3.7 17.0 3.8 4.1 2.3
5.3 7.8 8.1 4.3 13.3 6.8 1.3 7.0 4.9 1.8 7.1 28.0 10.2 13.8 17.9 10.1 5.5 4.6 3.2 21.6
【例】利用9.2.1节中100户居民的月均用水量的调查数据,计算样本数据的众数、平均数和中位数,并据此估计全市居民用户月均用水量的众数、中位数和平均数。
中位数
众数
平均数
众数是2.0和5.5
中位数是
因为数据是抽自全市居民的简单随机样本,所以我们可以据
此估计全市居民用户的月均用水量的众数约为2.0t和5.5t,平均数约为8.79t,其中位数约为6.8t.
探究二:众数、中位数、平均数与频率分布直方图的关系
在某些情况下我们无法获知原始的样本数据。这时该如何估计样本的众数、中位数、平均数?
你能以下面的频率分布直方图提供的信息为例,给出估计方法吗?
一组数据中出现次数最多的数
众数:在样本数据的频率分布直方图中,最高矩形的中点的横坐标。
月均用水量在区间[4.2,7.2)内的居民最多, 可以将这个区间的中点5.7作为众数的估计值.
1.估计众数
频数
频率
将一组数据按大小依次排列,把处在最中间位置的一个数据(或两个数据的平均数)叫做这组数据的中位数.
中位数:把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标。
50%
0.231
0.552
设中位数为 ,
解得
面积
2.估计中位数
3.估计平均数
设 为每一组的频数
中点yi'估计
频率
底边中点横坐标×小矩形面积
n1
y1’
平均数:等于各小矩形的面积乘以其底边中点的横坐标之和。
中点yi'估计
3.估计平均数
由频率分布直方图我们估计出全市居民用户月均用水量的众数是5.7,中位数是6.71,平均数是8.96.
频率分布直方图
众数 5.7
中位数 6.71
平均数 8.96
原始数据
2.0、5.5
6.8
8.79
比较从居民月均用水量样本数据计算出的该样本的众数、中位数、平均数与我们从样本频率分布直方图得出的结论,你发现了什么?
频率分布直方图损失了一些样本数据,得到的是一个估计值,所得估值与数据分组有关.
探究三:众数、中位数、平均数分析
名称 优点 缺点
众数
1. 特征
它只能表达样本数据中很少的一部分信息,无法客观的反映总体的特征.
(1)众数
1.体现样本数据的最大
集中点;
2.容易计算;
3.不受极端值影响.
小明用统计软件计算100户居民用水量的平均数和中位数,但在录入数据时,不小心将一个数据7.7录成了77,请计算录入数据的平均数和中位数,并与真实的样本平均数和中位数作比较,哪个量的值变化更大?你能解释其中的原因吗?
平均数
对极端数据更加敏感
(2)中位数、平均数
名称 优点 缺点
众数
中位数
平均数
1.体现样本数据的最大集中点;
2.容易计算.
它只能表达样本数据中很少的一部分信息,无法客观的反映总体的特征.
1.不受少数几个极端数的影响;
2.容易计算,利用中间数据的信息,反映中等水平.
对极端数据不敏感.
代表性较好,是反映数据集中趋势的量.一般情况下,可以反映更多的根源样本数据全体的信息.
任何一个数据的改变都会引起平均数的改变,数据越“离群”,对平均数的影响越大.
3.不受极端值影响.
例5:某学校要定制高一年级的校服,学生根据厂家提供的参考身高选择校服规格,据统计,高一年级女生需要不同规格校服的频数如表所示。
校服规格 155 160 165 170 175 合计
频数 39 64 167 90 26 386
如果用一个量来代表该校高一年级女生所需校服的规格,那么在中位数、平均数和众数中哪个量比较合适?试讨论用表中的数据估计全国高一年级女生校服规格的合理性。
2. 集中趋势的选择
校服规格 155 160 165 170 175 合计
频数 39 64 167 90 26 386
用众数165作为该校高一年级女生校服的规格比较合适.
由于全国各地的高一年级女生身高存在一定的差异,所以用一个学校的数据估计全国高一年级女生的校服规格不合理.
xs
对分类型数据集中趋势的描述,可以用众数.
校服规格
性别
产品质量等级
如:
视频来源:智联招聘、新浪财经(如图标注)
对数值型数据集中趋势的描述,可以用平均数、中位数.
用水量
身高
产量
如:
收入
所以,我们要强调”用数据说话”,但同时又要防止被误导。
课堂小结
集中
趋势
众数
平均数
中位数
课堂小结
统计的基本思想方法:
抽样收集数据
分析样本数据
对总体进行估计
数据
图表
谢 谢 !
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
