1.4-长方体和正方体的体积(课件)六年级上册数学苏教版(共39张PPT)
文档属性
| 名称 | 1.4-长方体和正方体的体积(课件)六年级上册数学苏教版(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 656.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-01 00:00:00 | ||
图片预览











文档简介
(共39张PPT)
苏 教 版 · 第 一 单 元 :长方体和正方体
长方体和正方体的体积
【学习重点】
掌握长方体、正方体体积公式,并能利用公式解决实际问题。
【学习难点】
长方体、正方体体积公式的由来和运用。
重难点
目录
contents
知识讲解
实战演练
Chapter 1
知识讲解
下图中的长方体是由1立方厘米的小正方体摆成的。它的长、宽、高各是多少厘米?摆这个长方体用了多少个1立方厘米的小正方体?它的体积是多少立方厘米?
长方体的体积
1cm 的小正方体棱长是1cm,这个长方体的长边摆了3个小正方体,宽和高所在的边均摆了2个小正方体,共由12个小正方体摆成
那就可以知道这个长方体的长是3cm,宽是2cm,高是2cm,它的体积是12cm
长方体的体积
刚才是由12个体积是1cm 的小正方体摆成的长方体,它的体积是12cm ,那12个1cm 的小正方体摆成长方体只有这一种摆法么?
当然不是啦!但是不管最后长方体的长宽高各是多少厘米,只要由12个体积是1cm 的小正方体摆成,它们的体积都是12cm
长方体的体积
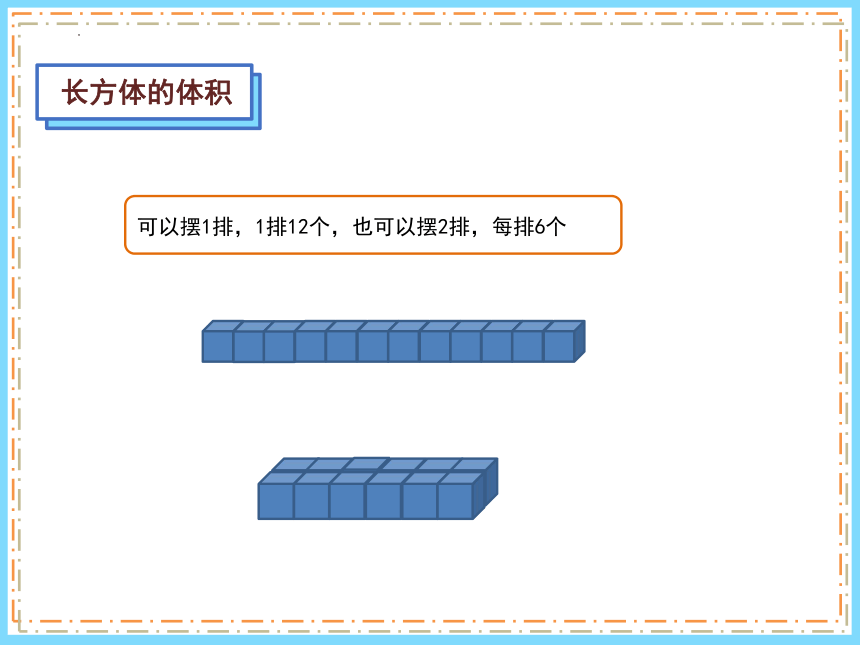
可以摆1排,1排12个,也可以摆2排,每排6个
长方体的体积
还可以摆3排,每排3个,或者摆3层,每层4个
长方体的体积
长/cm 宽/cm 高/cm 小正方体的个数/个 体积/cm
长方体① 12 1 1 12 12
长方体② 6 2 1 12 12
长方体③ 4 3 1 12 12
长方体④ 2 2 3 12 12
把每次拼摆的结果记录下来,汇成表格,然后观察表格,你能发现什么规律吗?
长方体的体积
每个长方体所含有1立方厘米的小正方体的个数或体积都正好等于长方体长、宽、高的乘积
在摆成的每个长方体中,每排小正方体的个数相当于长方体的长,排数相当于长方体的宽,层数相当于长方体的高
长方体的体积
长方体所含体积单位的数量就是长方体的体积,等于长方体的长、宽、高的乘积,由此可以得出长方体的体积=长×宽×高
长方体的体积
如果用V表示长方体的体积,用a,b,h来分别表示长方体的长、宽、高,那么长方体体积公式可以写成V=abh
a
b
h
长方体的体积
知识小结
长方体的体积=长×宽×高,用字母表示为V=abh。
根据长方体体积公式,你能自己推导出正方体的体积怎么计算吗?
正方体的体积
正方体是长宽高都相等的特殊长方体,所以正方体体积=棱长×棱长×棱长
长方体的体积= 长 × 宽 × 高
正方体的体积=棱长×棱长×棱长
正方体的体积
a
a
a
用V表示它的体积,a表示正方体的棱长,那正方体体积用字母表示就是V=a·a·a=a
正方体的体积
求出下图中阴影部分的面积及立体图形的体积。
(1)
(2)
阴影部分的面积就是长方体、正方体的底面积
正方体的体积
这两个图形的阴影部分就是一个平面图形,按照长方形和正方形面积公式去计算就可以
(1)阴影部分面积=5×3=15
(2)阴影部分面积=3×3=9
正方体的体积
求长方体、正方体体积直接把数字代入长方体、正方体的体积公式就能计算出来
V=5×3×4=60
(2) V=3×3×3=27
正方体的体积
长方体的体积=长×宽×高
底面积×高
正方体的体积=棱长×棱长×棱长
底面积 ×棱长(高)
长方体、正方体的体积=底面积×高
正方体的体积
知识小结
正方体的体积=棱长×棱长×棱长,用字母表示为:V=a·a·a=a 。
长方体、正方体的体积=底面积×高,用字母表示为:V=Sh(V表示底面积,h表示高)。
某家具厂要订购600根同样的方木,每根方木横截面的面积是25dm2,长是2m,这些方木一共有多少立方米?
经典例题
方木的横截面相当于长方体的底面积,方木的长就等于长方体的高,根据V=Sh先求出方木的体积,再乘上600就可以得到600根方木有多少立方米
25平方分米=0.25平方米
0.25×2×600
=0.5×600
=300(立方米)
答:这些方木一共有300立方米。
一块正方体的石料,棱长4分米,如果1立方分米的石料重3千克,这块石料重多少千克?
经典例题
首先根据正方体的体积公式:v=a3,求出石料的体积,然后乘3千克即可得到石料的重量
4×4×4×3
=64×3
=192(千克)
答:这块石料重192千克。
知识小结
已知长方体、正方体物体的长、宽、高或棱长时,可以直接利用公式计算物体的体积。
Chapter 2
实战演练
1.选择题
(1)既有容积又有体积的物体,在不忽略容器壁的厚度的情况下,体积一般( )容积。
A.大于 B.等于 C.小于
(2)把一个正方体的棱长扩大3倍,那么它的体积扩大( )倍。
A.6 B.9 C.27
课堂检测
【答案】
(1)A
(2)C
课堂检测
2.判断。
(1)所有物体都有容积与体积。 ( )
(2)棱长为6cm的正方体的体积与表面积相等。 ( )
(3)一个体积是1立方厘米的物体,它一定是一个棱长1厘米的正方体。 ( )
(4)把一块正方体橡皮泥捏成长方体后,虽然它的形状变了,但它的体积不变。 ( )
课堂检测
【答案】
(1)×
(2)×
(3)×
(4)√
课堂检测
3.有一堆砂共120m3,要把它铺在长300m,宽4m的跑道上,可以铺多厚?
课堂检测
3.有一堆砂共120m3,要把它铺在长300m,宽4m的跑道上,可以铺多厚?
【答案】
120÷300÷4=0.1(米)
答:可以铺0.1米厚。
课堂检测
4.一根长为6m的木料,横截面是边长为30cm的正方形,这根木料的体积是多少立方厘米?合多少立方分米?
课堂检测
4.一根长为6m的木料,横截面是边长为30cm的正方形,这根木料的体积是多少立方厘米?合多少立方分米?
【答案】
6米=600厘米
30×30×600=540000(立方厘米)=540立方分米
答:这根木料的体积是540000立方厘米,合540立方分米。
课堂检测
5.把一个棱长为20cm的正方体铁块锻造成长40cm,宽25cm的长方体,长方体铁块的高是多少?
课堂检测
【答案】
20×20×20÷(40×25)=8(cm)
答:长方形的高是8cm。
【解析】
把正方体钢材锻造成长方体只是形状变了,但体积不变。首先根据正方体的体积公式:v=a3,求出钢材的体积,再根据长方体的体积公式:V=Sh,用钢材体积除以长方体的底面积即可。
课堂检测
1
总 结
2
3
正方体的体积=棱长×棱长×棱长,用字母表示为:V=a·a·a=a 。
长方体的体积=长×宽×高,用字母表示为V=abh。
长方体、正方体的体积=底面积×高,用字母表示为:V=Sh(V表示底面积,h表示高)。
苏 教 版 · 第 一 单 元 :长方体和正方体
长方体和正方体的体积
【学习重点】
掌握长方体、正方体体积公式,并能利用公式解决实际问题。
【学习难点】
长方体、正方体体积公式的由来和运用。
重难点
目录
contents
知识讲解
实战演练
Chapter 1
知识讲解
下图中的长方体是由1立方厘米的小正方体摆成的。它的长、宽、高各是多少厘米?摆这个长方体用了多少个1立方厘米的小正方体?它的体积是多少立方厘米?
长方体的体积
1cm 的小正方体棱长是1cm,这个长方体的长边摆了3个小正方体,宽和高所在的边均摆了2个小正方体,共由12个小正方体摆成
那就可以知道这个长方体的长是3cm,宽是2cm,高是2cm,它的体积是12cm
长方体的体积
刚才是由12个体积是1cm 的小正方体摆成的长方体,它的体积是12cm ,那12个1cm 的小正方体摆成长方体只有这一种摆法么?
当然不是啦!但是不管最后长方体的长宽高各是多少厘米,只要由12个体积是1cm 的小正方体摆成,它们的体积都是12cm
长方体的体积
可以摆1排,1排12个,也可以摆2排,每排6个
长方体的体积
还可以摆3排,每排3个,或者摆3层,每层4个
长方体的体积
长/cm 宽/cm 高/cm 小正方体的个数/个 体积/cm
长方体① 12 1 1 12 12
长方体② 6 2 1 12 12
长方体③ 4 3 1 12 12
长方体④ 2 2 3 12 12
把每次拼摆的结果记录下来,汇成表格,然后观察表格,你能发现什么规律吗?
长方体的体积
每个长方体所含有1立方厘米的小正方体的个数或体积都正好等于长方体长、宽、高的乘积
在摆成的每个长方体中,每排小正方体的个数相当于长方体的长,排数相当于长方体的宽,层数相当于长方体的高
长方体的体积
长方体所含体积单位的数量就是长方体的体积,等于长方体的长、宽、高的乘积,由此可以得出长方体的体积=长×宽×高
长方体的体积
如果用V表示长方体的体积,用a,b,h来分别表示长方体的长、宽、高,那么长方体体积公式可以写成V=abh
a
b
h
长方体的体积
知识小结
长方体的体积=长×宽×高,用字母表示为V=abh。
根据长方体体积公式,你能自己推导出正方体的体积怎么计算吗?
正方体的体积
正方体是长宽高都相等的特殊长方体,所以正方体体积=棱长×棱长×棱长
长方体的体积= 长 × 宽 × 高
正方体的体积=棱长×棱长×棱长
正方体的体积
a
a
a
用V表示它的体积,a表示正方体的棱长,那正方体体积用字母表示就是V=a·a·a=a
正方体的体积
求出下图中阴影部分的面积及立体图形的体积。
(1)
(2)
阴影部分的面积就是长方体、正方体的底面积
正方体的体积
这两个图形的阴影部分就是一个平面图形,按照长方形和正方形面积公式去计算就可以
(1)阴影部分面积=5×3=15
(2)阴影部分面积=3×3=9
正方体的体积
求长方体、正方体体积直接把数字代入长方体、正方体的体积公式就能计算出来
V=5×3×4=60
(2) V=3×3×3=27
正方体的体积
长方体的体积=长×宽×高
底面积×高
正方体的体积=棱长×棱长×棱长
底面积 ×棱长(高)
长方体、正方体的体积=底面积×高
正方体的体积
知识小结
正方体的体积=棱长×棱长×棱长,用字母表示为:V=a·a·a=a 。
长方体、正方体的体积=底面积×高,用字母表示为:V=Sh(V表示底面积,h表示高)。
某家具厂要订购600根同样的方木,每根方木横截面的面积是25dm2,长是2m,这些方木一共有多少立方米?
经典例题
方木的横截面相当于长方体的底面积,方木的长就等于长方体的高,根据V=Sh先求出方木的体积,再乘上600就可以得到600根方木有多少立方米
25平方分米=0.25平方米
0.25×2×600
=0.5×600
=300(立方米)
答:这些方木一共有300立方米。
一块正方体的石料,棱长4分米,如果1立方分米的石料重3千克,这块石料重多少千克?
经典例题
首先根据正方体的体积公式:v=a3,求出石料的体积,然后乘3千克即可得到石料的重量
4×4×4×3
=64×3
=192(千克)
答:这块石料重192千克。
知识小结
已知长方体、正方体物体的长、宽、高或棱长时,可以直接利用公式计算物体的体积。
Chapter 2
实战演练
1.选择题
(1)既有容积又有体积的物体,在不忽略容器壁的厚度的情况下,体积一般( )容积。
A.大于 B.等于 C.小于
(2)把一个正方体的棱长扩大3倍,那么它的体积扩大( )倍。
A.6 B.9 C.27
课堂检测
【答案】
(1)A
(2)C
课堂检测
2.判断。
(1)所有物体都有容积与体积。 ( )
(2)棱长为6cm的正方体的体积与表面积相等。 ( )
(3)一个体积是1立方厘米的物体,它一定是一个棱长1厘米的正方体。 ( )
(4)把一块正方体橡皮泥捏成长方体后,虽然它的形状变了,但它的体积不变。 ( )
课堂检测
【答案】
(1)×
(2)×
(3)×
(4)√
课堂检测
3.有一堆砂共120m3,要把它铺在长300m,宽4m的跑道上,可以铺多厚?
课堂检测
3.有一堆砂共120m3,要把它铺在长300m,宽4m的跑道上,可以铺多厚?
【答案】
120÷300÷4=0.1(米)
答:可以铺0.1米厚。
课堂检测
4.一根长为6m的木料,横截面是边长为30cm的正方形,这根木料的体积是多少立方厘米?合多少立方分米?
课堂检测
4.一根长为6m的木料,横截面是边长为30cm的正方形,这根木料的体积是多少立方厘米?合多少立方分米?
【答案】
6米=600厘米
30×30×600=540000(立方厘米)=540立方分米
答:这根木料的体积是540000立方厘米,合540立方分米。
课堂检测
5.把一个棱长为20cm的正方体铁块锻造成长40cm,宽25cm的长方体,长方体铁块的高是多少?
课堂检测
【答案】
20×20×20÷(40×25)=8(cm)
答:长方形的高是8cm。
【解析】
把正方体钢材锻造成长方体只是形状变了,但体积不变。首先根据正方体的体积公式:v=a3,求出钢材的体积,再根据长方体的体积公式:V=Sh,用钢材体积除以长方体的底面积即可。
课堂检测
1
总 结
2
3
正方体的体积=棱长×棱长×棱长,用字母表示为:V=a·a·a=a 。
长方体的体积=长×宽×高,用字母表示为V=abh。
长方体、正方体的体积=底面积×高,用字母表示为:V=Sh(V表示底面积,h表示高)。
