1.5 圆周率的历史(教学课件)六年级数学上册 北师大版(共35张PPT)
文档属性
| 名称 | 1.5 圆周率的历史(教学课件)六年级数学上册 北师大版(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-01 00:00:00 | ||
图片预览










文档简介
(共35张PPT)
圆周率的历史
小学数学·六年级(上)
北师大版·第一单元
阅读圆周率的发展简史,感受数学知识的探索过程, 了解圆周率的研究史上的相关知识及做出重要贡献的人物和研究方法。
通过自主搜集圆周率的相关资料、交流体验,培养收集信息、整合信息,提高质疑、理解的能力。
结合圆周率发展历史的阅读,体会人类对数学知识的不断探索过程,感受数学文化的魅力。
重
两种分类了解数学发展的方法,怎样分类。
了解数学史上,哪些重要的数学家做出的哪些重要贡献。
这是个
没有
圆
的世界
如果没有π,世界会怎样?
欧几里德
几何原本
π
欧几里德·著
公元前30年,欧几里德在《几何原本》上写到:圆周率是常数。
中国古算书《周髀算经》( 约公元前2世纪)中有“径一而周三”的记载,也认为圆周率是常数。
周簰算經
早期大都是通过实验而得到的结果,如古埃及纸草书(约公元前1700)中取π=(4/3)^4≈3.1604 。
ΗΘΩΚ фжΩ√Τζ λφ
人类的祖先在实践中发现,不同粗细的圆木,用绳子绕上一圈,绳子的长度总是圆木直径的3倍多一点。
用测量的方法计算圆周率,圆周率的精确程度取决于测量的精确程度。
我国魏晋时期的数学家刘徽创造了“割圆术”求圆周率的方法。刘徽是怎样“割圆”的呢?
刘徽用这种方法不断地“割圆”,一直算到圆内接正192边形,得到圆周率的近似值是3.14。
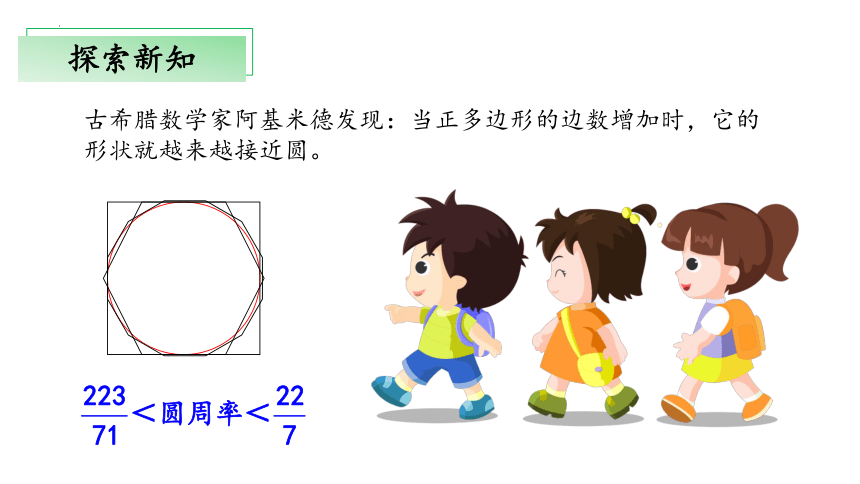
古希腊数学家阿基米德发现:当正多边形的边数增加时,它的形状就越来越接近圆。
古希腊的阿基米德和我国古代的刘徽想到的计算圆周率的方法在本质上是一致的。
约1500年前,中国有一位伟大的数学家和天文学家祖冲之。他计算出圆周率应在3.1415926 和3.1415927 之间,成为世界上第一个把圆周率的值计算精确到7 位小数的人。
这一成就,使中国在圆周率的计算方面在世界领先1000年。
据专家推测,“缀术”类似“割圆术”,通过对正24576边形周长的计算来推导。计算相当繁杂,当时还没有算盘。
电子计算机的出现带来了计算方面的革命,圆周率的小数点后面的精确数字越来越多。
到2002年,圆周率已经可以计算到小数点后12411亿位。
你能背出多少位圆周率?
1.圆周率的发展历史已经有几千年了,我国在圆周率的研究方面取得了举世瞩目的成就。
2.古代数学家刘徽、祖冲之计算出圆周率的精确程度比其他国家要早很多年。
3.计算机的出现使圆周率的计算更为精确,到2000年已经达到小数点后面的12411亿位。
1736年以后开始使用“π”表示圆周率。
英国数学家首先使用 表示圆周率。π是希腊文圆周的第一个字母,而 是希腊文直径的第一个字母。当直径是1时, 。
收集其他有关圆周率的历史资料,在班上进行展示。
圆周率的计算历史
时间 纪录创造者 小数点后位数
前2000 古埃及 1
前1200 中国 1
前500 圣经 1
前250 Archimedes 3
前263 刘徽 5
480 祖冲之 7
1429 Al-Kashi 14
…
…
…
1.填空。
(1)用圆规画一个圆,如果圆规两脚间的距离是4 cm,那么这个圆的周长是( )cm。
(2)一个圆的直径是5 cm,它的周长是( )cm。
2.选择。
(1)一个圆的半径扩大到原来的4倍,它的周长就扩大到原来的( )倍。
A.4 B.6 C.10 D.16
25.12
15.7
A
(2)小圆的直径和大圆的半径都是4 cm,小圆的周长是大圆的周长的( )。
(3)一个圆,如果半径增加1 dm,那么周长增加( )dm。
A.2 B.π C.2π D.3π
A
C
3.计算下面各圆的周长。
2×3.14×3=18.84(cm)
8×3.14=25.12(m)
4.解决问题。
(1)学校有一个圆形的喷泉水池,半径是7.5 m。现要在它的边缘围上一圈防护栏,防护栏的长是多少米?
2×3.14×7.5=47.1(m)
(2)车轮滚动一周前进了多少米?
3.14×70=219.8(cm)=2.198(m)
(3)在一个半径是40 m的圆形池塘边缘栽一圈树,每隔6.28 m栽一棵,一共可以栽多少棵树?
2×3.14×40÷6.28=40(棵)
5.计算下面图形阴影部分的周长。
(1)
(2)
3.14×(1.5+5)÷2+3.14×
1.5÷2+3.14×5÷2=20.41
3.14×8+13×2=51.12
1.了解圆周率的研究史上的相关知识。
2.了解作出重要贡献的人物和研究方法。
3.求组合图形或不规则图形的周长时,可以采用转化法把它转化成规则图形。
1.钟表的分针长4厘米,计算针尖所走的路程是算什么?(请按要求填写下表)
602.88cm
576cm
192π
一天
12.56cm
12cm
4π
半小时
125.6cm
120cm
40π
5小时
25.12cm
24cm
8π
1小时
Π取3.14
Π取3
精确到π
钟表所走时间
2.钟表的时针长10厘米,时针扫过的面积指的是什么?
157cm
50π
3时~9时
78.5cm
25π
12时~15时
314cm
100π
半天
628cm
200π
一天
Π取3.14
结果精确到π
时钟所走时间
小芳从家到学校的距离约1100米,一辆自行车车轮胎的外直径约0.7米,小芳骑自行车每分钟转100周,从家到学校几分钟?
3.请选择合适的π的近似值计算下题:
22
7
355
113
3
3.14
1100÷(0.7×3.14×100)≈5(分)答:从家到学校5分钟。
注意:在有关圆的计算中,先用π表示出计算结果,再根据题目的要求来选择圆周率的近似值来进行计算;
4.用含有π的式子表示填写下表
圆的周长是直径的( )倍;
圆的周长是半径的( )倍;
半圆的周长是它的直径的( )倍;
半圆的周长是它的半径的( )倍;
π
2 π
π+2
5.中大圆周长比小圆长多少厘米?
15×2×3.14-10×2×3.14=31.4(厘米)答:大圆周长比小圆长31.4厘米。
作业:通过这节课的学习你想提醒同学们在兑换人民的过程中应注意什么
Thank you!
圆周率的历史
小学数学·六年级(上)
北师大版·第一单元
阅读圆周率的发展简史,感受数学知识的探索过程, 了解圆周率的研究史上的相关知识及做出重要贡献的人物和研究方法。
通过自主搜集圆周率的相关资料、交流体验,培养收集信息、整合信息,提高质疑、理解的能力。
结合圆周率发展历史的阅读,体会人类对数学知识的不断探索过程,感受数学文化的魅力。
重
两种分类了解数学发展的方法,怎样分类。
了解数学史上,哪些重要的数学家做出的哪些重要贡献。
这是个
没有
圆
的世界
如果没有π,世界会怎样?
欧几里德
几何原本
π
欧几里德·著
公元前30年,欧几里德在《几何原本》上写到:圆周率是常数。
中国古算书《周髀算经》( 约公元前2世纪)中有“径一而周三”的记载,也认为圆周率是常数。
周簰算經
早期大都是通过实验而得到的结果,如古埃及纸草书(约公元前1700)中取π=(4/3)^4≈3.1604 。
ΗΘΩΚ фжΩ√Τζ λφ
人类的祖先在实践中发现,不同粗细的圆木,用绳子绕上一圈,绳子的长度总是圆木直径的3倍多一点。
用测量的方法计算圆周率,圆周率的精确程度取决于测量的精确程度。
我国魏晋时期的数学家刘徽创造了“割圆术”求圆周率的方法。刘徽是怎样“割圆”的呢?
刘徽用这种方法不断地“割圆”,一直算到圆内接正192边形,得到圆周率的近似值是3.14。
古希腊数学家阿基米德发现:当正多边形的边数增加时,它的形状就越来越接近圆。
古希腊的阿基米德和我国古代的刘徽想到的计算圆周率的方法在本质上是一致的。
约1500年前,中国有一位伟大的数学家和天文学家祖冲之。他计算出圆周率应在3.1415926 和3.1415927 之间,成为世界上第一个把圆周率的值计算精确到7 位小数的人。
这一成就,使中国在圆周率的计算方面在世界领先1000年。
据专家推测,“缀术”类似“割圆术”,通过对正24576边形周长的计算来推导。计算相当繁杂,当时还没有算盘。
电子计算机的出现带来了计算方面的革命,圆周率的小数点后面的精确数字越来越多。
到2002年,圆周率已经可以计算到小数点后12411亿位。
你能背出多少位圆周率?
1.圆周率的发展历史已经有几千年了,我国在圆周率的研究方面取得了举世瞩目的成就。
2.古代数学家刘徽、祖冲之计算出圆周率的精确程度比其他国家要早很多年。
3.计算机的出现使圆周率的计算更为精确,到2000年已经达到小数点后面的12411亿位。
1736年以后开始使用“π”表示圆周率。
英国数学家首先使用 表示圆周率。π是希腊文圆周的第一个字母,而 是希腊文直径的第一个字母。当直径是1时, 。
收集其他有关圆周率的历史资料,在班上进行展示。
圆周率的计算历史
时间 纪录创造者 小数点后位数
前2000 古埃及 1
前1200 中国 1
前500 圣经 1
前250 Archimedes 3
前263 刘徽 5
480 祖冲之 7
1429 Al-Kashi 14
…
…
…
1.填空。
(1)用圆规画一个圆,如果圆规两脚间的距离是4 cm,那么这个圆的周长是( )cm。
(2)一个圆的直径是5 cm,它的周长是( )cm。
2.选择。
(1)一个圆的半径扩大到原来的4倍,它的周长就扩大到原来的( )倍。
A.4 B.6 C.10 D.16
25.12
15.7
A
(2)小圆的直径和大圆的半径都是4 cm,小圆的周长是大圆的周长的( )。
(3)一个圆,如果半径增加1 dm,那么周长增加( )dm。
A.2 B.π C.2π D.3π
A
C
3.计算下面各圆的周长。
2×3.14×3=18.84(cm)
8×3.14=25.12(m)
4.解决问题。
(1)学校有一个圆形的喷泉水池,半径是7.5 m。现要在它的边缘围上一圈防护栏,防护栏的长是多少米?
2×3.14×7.5=47.1(m)
(2)车轮滚动一周前进了多少米?
3.14×70=219.8(cm)=2.198(m)
(3)在一个半径是40 m的圆形池塘边缘栽一圈树,每隔6.28 m栽一棵,一共可以栽多少棵树?
2×3.14×40÷6.28=40(棵)
5.计算下面图形阴影部分的周长。
(1)
(2)
3.14×(1.5+5)÷2+3.14×
1.5÷2+3.14×5÷2=20.41
3.14×8+13×2=51.12
1.了解圆周率的研究史上的相关知识。
2.了解作出重要贡献的人物和研究方法。
3.求组合图形或不规则图形的周长时,可以采用转化法把它转化成规则图形。
1.钟表的分针长4厘米,计算针尖所走的路程是算什么?(请按要求填写下表)
602.88cm
576cm
192π
一天
12.56cm
12cm
4π
半小时
125.6cm
120cm
40π
5小时
25.12cm
24cm
8π
1小时
Π取3.14
Π取3
精确到π
钟表所走时间
2.钟表的时针长10厘米,时针扫过的面积指的是什么?
157cm
50π
3时~9时
78.5cm
25π
12时~15时
314cm
100π
半天
628cm
200π
一天
Π取3.14
结果精确到π
时钟所走时间
小芳从家到学校的距离约1100米,一辆自行车车轮胎的外直径约0.7米,小芳骑自行车每分钟转100周,从家到学校几分钟?
3.请选择合适的π的近似值计算下题:
22
7
355
113
3
3.14
1100÷(0.7×3.14×100)≈5(分)答:从家到学校5分钟。
注意:在有关圆的计算中,先用π表示出计算结果,再根据题目的要求来选择圆周率的近似值来进行计算;
4.用含有π的式子表示填写下表
圆的周长是直径的( )倍;
圆的周长是半径的( )倍;
半圆的周长是它的直径的( )倍;
半圆的周长是它的半径的( )倍;
π
2 π
π+2
5.中大圆周长比小圆长多少厘米?
15×2×3.14-10×2×3.14=31.4(厘米)答:大圆周长比小圆长31.4厘米。
作业:通过这节课的学习你想提醒同学们在兑换人民的过程中应注意什么
Thank you!
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
